Учебный процесс вуза является сложным объектом управления, его эффективность зависит от многих факторов. В ходе проводимой реформы системы образования возникают проблемы повышения эффективности учебного процесса для повышения качества подготовки специалистов [1, 2]. Проведены исследования академической и социальной адаптации студентов [3], построены уравнения регрессии для связи результатов обучения с рядом факторов, оценено влияние информационных технологий на качество обучения. Статистические исследования результатов сессий показали влияние системы экзаменов на результаты обучения [4, 5]. Проведен анализ успеваемости студентов, изучены разные факторы, влияющие на успеваемость [6, 7]. Однако задачи оценки влияния организационных факторов на результаты экзаменов пока не решены, не разработаны критерии оценки эффективности таких факторов учебного процесса, как последовательность экзаменов, качество преподавания, формирование групп студентов. Реализации задач, стоящих перед образовательной системой РФ, возможна только при наличии в вузах современной, высококачественной и высокотехнологичной информационно-образовательной среды [8]. Рассмотрев степень разработанности изучаемой проблемы в России, можно отметить, что исследования влияющих на учебный процесс факторов пока не многочисленны и недостаточно конструктивны, что свидетельствует об актуальности научных исследований по данной теме. В статье поставлены и решены задачи анализа учебного процесса и даны конструктивные рекомендации по повышению показателей успеваемости студентов.
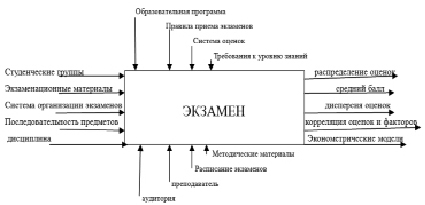
Рис. 1. Схематическое представление организации экзамена в вузе
Модель учебного процесса вуза
Учебный процесс представляет собой процесс:
P = (Х, Y, T, R, t), (1)
где Х – входы, Y – выходы или результаты процесса обучения, T – технология обучения (последовательность обучающих воздействий, определенная учебным планом), R – используемые ресурсы (преподаватели, методическое и техническое обеспечение, аудитории), t – время. Основным результатом применяемой технологии является средний балл успеваемости, который зависит от многих факторов:
Mb = f(QОбПр, Qмет, Qпреп,
OУпПр, Oэкз, M, C, Qабит, G), (2)
где QОбПр – качество образовательной программы; Qмет – качество методического обеспечения; Qпреп – уровень и качество преподавания; OУпПр – уровень организации учебного процесса; Oэкз – уровень организации экзаменов в вузе; М – показатель мотивации и интереса студентов к обучению; С – сложность изучаемой дисциплины; Qабит – качество подготовки абитуриентов; G – показатель организации студенческих групп. Итоговые показатели в значительной степени зависят от организации экзаменов в вузе (рис. 1).
На результаты экзаменов оказывают влияние большое число объектов, процессов, факторов и условий различной природы. Экзамен проходит в студенческих группах, что усложняет применение стандартного аппарата параметрических статистик для анализа результатов. В [8] отмечается известный в психологии факт, что реальные законы, управляющие поведением людей в группах, сложнее, чем описываемые нормальным законом распределения. Но рассматривая учебную группу как некий интегратор этих процессов, можно предположить, что такие социальные группы могут быть классифицированы и могут иметь достаточно предсказуемое поведение. Будем рассматривать такие элементы учебного процесса, как 1) учебная группа; 2) экзаменатор (преподаватель); 3) дисциплина (предмет); 4) расписание экзаменов (сессии). Для повышения качества показателей обучения нужна система поддержки образовательного процесса» (СПОП), которая на основании статистического изучения влияния различных факторов на результаты процесса будет выбирать такие значения управляющих воздействий, которые позволят повысить эффективность обучения. Схематически эту систему можно представить рис. 2.
Система поддержки процесса обучения СПОП (рис. 2) включает четыре подсистемы и должна решить задачу формирования оптимального процесса обучения. Каждая специальность Ai требует определенных знаний Cik. В зависимости от уровня сложности деятельности состав и соотношение разных знаний меняются. Взаимосвязи курсов образовательной программы Пr отображаются ориентированным графом Ст(П, U), где U = {Uij} множество дуг, характеризующих связи курсов. Если Пi и Пj имеют дугу Uij, то Пi > П, и последовательность связей П1 > П2>…> Пn формирует допустимую последовательность курсов. Таким образом, изучаемые дисциплины должны быть структурированы и упорядочены. В процессе обучения структура знаний должна быть согласована с возможностями их усвоения студентом. Для этого нужно минимизировать временные разрывы между курсами Тij с учетом их весов wij:
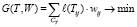(3)
при ограничениях времени занятий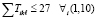 
отведенных на дисциплину часов 
.
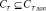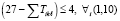. (4)
Решение этой задачи позволяет адаптировать расписания занятий к характеристикам обучающихся.
Статистический анализ степени удовлетворенности студентов
Поскольку мотивация студентов играет решающую роль в успехе обучения, был произведен анкетный опрос семи студенческих групп РГЭУ для получения оценок четырех факторов процесса обучения: организации учебного процесса x1, качества методического обеспечения x2, индивидуальной работы со студентами x3 и уровня преподавателей x4 [9]. Выборка достаточна (р > 0,9), студенты давали оценки по пятибалльной шкале. Результаты обработки показали средние оценки факторов (рис. 3).
Рис. 3 свидетельствует о том, что несмотря на положительные личностные качества преподавателей, студенты все же не удовлетворены непосредственно участием педагогов в работе с ними. Считая результатами обучения средние оценки опрошенных студентов yi и учитывая влияния на них оцениваемых факторов, рассчитаем модель регрессии:
Yi = 1,6 + 0,31x1 + 0,66x2 + 0,53x3 + 0,79x4;
R2 = 0,8573. (5)
Все факторы влияют на средний балл положительно, особенно уровень преподавателей. Поскольку в анализируемой статистике имеется конечное количество состояний студентов bj, соответствующих баллам 3, 4 и 5, можно рассчитать соответствующие им вероятности появления этих событий. Примем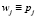 
. Теперь вычислим энтропию для каждой дисциплины по формуле
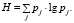(6)
Так как все pj < 1, то десятичные логарифмы от pj будут меньше нуля. Поэтому возьмем для расчетов абсолютное значение энтропии. Расчеты энтропий распределений оценок студентов для разных дисциплин существенно различались, что характеризует сложность изучаемых дисциплин, а изменения энтропии во времени показывает рост организации и уровня знаний дисциплин. Результаты вычислений приведем в табл. 1.
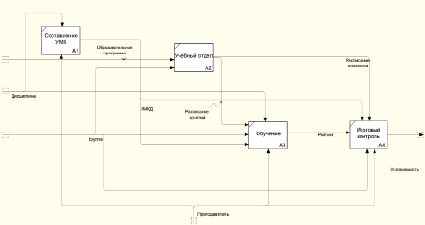
Рис. 2. Функциональная модель СПОП
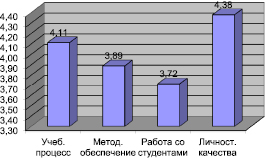
Рис. 3. Средние оценки факторов учебного процесса студентами
Таблица 1
Значения энтропии по дисциплинам и учебным годам
|
№ п/п |
Предметы |
Энтропия распределений оценок Hi |
||
|
2013–2014 |
2014–2015 |
2015–2016 |
||
|
1 |
Экономическая теория |
0,436 |
0,469 |
0,477 |
|
2 |
Математическое программирование |
0,377 |
0,383 |
0,435 |
|
3 |
Управление офисом |
0,461 |
0,422 |
0,427 |
|
4 |
Логические методы в менеджменте |
0,407 |
0,39 |
0,449 |
|
5 |
Теория вероятностей и мат статистика |
0,359 |
0,473 |
0,469 |
Чем выше энтропия предмета, тем более его неупорядоченность, чем меньше энтропия – тем меньше разброс значений вокруг средних значений (меньше дисперсия). Мера неупорядоченности дисциплин по годам уменьшается, что говорит о росте упорядоченности оценок и знаний студентов.
Математическая модель метода прогнозирования результатов сессии
Можно выдвинуть гипотезу о зависимости средних баллов студентов от последовательности экзаменов, которая была подтверждена на основе статистической проверки этой гипотезы [10]. Нулевые гипотезы H01, H02 и H03 не могут быть приняты, и успеваемость групп зависит от преподавателей, дисциплин и последовательности экзаменов.
Для построения модели прогнозирования оценок на экзаменах от их порядка введем следующие определения: Xts – значение ранга экзамена, Xs – значение ранга дисциплины, Xt – значение ранга экзаменатора. Рассмотрим мультипликативную композицию факторов в виде
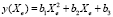. (7)
Будем рассчитывать показатель Xt по формуле
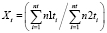, (8)
где nt – число экзаменов, которые принял преподаватель t;
n1ti – число отрицательных оценок, которые поставил преподаватель t на экзамене i;
n2ti – общее число оценок, которые должен был поставить преподаватель t на экзамене i;
Аналогично находится ранг дисциплины Xs. Основываясь на предположении о влиянии расписания экзаменов на их результат [10], представим эту часть регрессионной модели в виде многочлена второго порядка от номера экзамена (Xe) в расписании сессии группы.
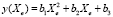. (9)
Окончательно получим вид регрессионной модели для выходной переменной с помощью мультипликативной свертки гибридной переменной Xts и квадратного трехчлена:
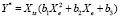, (10)
где Y* – оценка успеваемости учебной группы на экзамене, который проводил преподаватель t, по дисциплине s, Xts – ранг экзамена; Xe – номер экзамена в расписании сессии, b1, b2, b3 – коэффициенты регрессии.
Уравнение регрессии (10) преобразуем в линейную форму с помощью вспомогательных переменных:
; 
; 
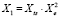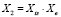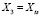. (11)
В результате выполненных преобразований, уравнение регрессии (10) приобретает следующий вид:
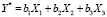. (12)
Уравнение в виде (10) назовем базовым уравнением регрессии, а уравнение (12) – вспомогательным уравнением регрессии.
Энтропийные оценки эффекта последовательности экзаменов
Стратегия управления учебным процессом заключается в выборе таких значений управляющих переменных процесса, которые дают наилучший ожидаемый результат. Для оценки эффекта применения более адаптивной к условиям вуза последовательности экзаменов в сессию были выбраны данные о результатах 132 групп студентов ДГТУ в зимнюю сессию 2013–2014 года. Выбраны только группы с четырьмя экзаменами. Статистика достаточна с р > 0,9. Для расчета прогнозов успеваемости групп на сессии использована описанная выше регрессионная модель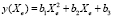 
. Рассчитаны средние значения оценок для всех групп (табл. 2). Для выбора оптимальной последовательности экзаменов рассчитаны все варианты расписания (24 сочетания): {{1,2,3,4},{1,2,4,3},{1,4,2,3},{4,1,2,3},…{4,3,2,1}}.
Находится расписание с максимальным процентом успешных сдач сессии и для каждой группы рассчитаны два значения: реальные средние баллы и проценты успешных экзаменов (табл. 2). По формуле энтропии
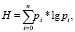(13)
где pi – доля оценок по сессиям; n – количество групп, рассчитаны энтропии распределений реальных оценок 132 групп студентов ДГТУ и прогнозируемые результаты и энтропии для наиболее эффективной последовательности экзаменов (табл. 2).
Таблица 2
Результаты расчетов реальных и прогнозируемых средних оценок и энтропий для рекомендуемой последовательности экзаменов (для четырех студенческих групп)
|
Реальные показатели успеваемости групп |
Прогнозируемые показатели групп |
Реальный средний балл группы |
Прогнозируемый средний балл группы |
Реальное значение энтропии распределения оценок группы, хартли |
Расчетная энтропия прогнозируемого распределения оценок, хартли |
Изменение (энтропии при применении рекомендуемой последовательности экзаменов, хартли |
|
71,1 |
71,3 |
3,52 |
3,57 |
1,96 |
1,92 |
0,04 |
|
81,71 |
82,1 |
4,08 |
4,11 |
2,51 |
2,49 |
0,02 |
|
54,8 |
56,2 |
2,7 |
2,8 |
1,26 |
1,20 |
0,06 |
|
88,1 |
88,5 |
4,2 |
4,4 |
2,83 |
2,85 |
0,03 |
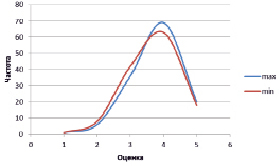
Рис. 4. Распределение оценок по максимальному и реальному расписанию
Результаты расчетов показали, что действительно при применении основанной моделированием последовательности экзаменов средние показатели успешности сдачи экзаменов, средние баллы увеличиваются, что отражается в снижении расчетных показателей энтропии. Суммарная энтропия реальных распределений оценок 132 групп равна 221,4 хартли, прогнозируемых распределений 215,22 хартли. Применение рекомендованной последовательности экзаменов снизило энтропию распределений на ΔH = 6,14 хартли. Качественные изменения видны при сравнении распределений оценок (рис. 4).
Выводы
1. Внутренними факторами, которые наиболее явно влияют на успеваемость студентов, являются факторы качества организации учебного процесса и последовательность экзаменов.
2. Задачи построения расписаний занятий и экзаменов сходны по постановке, целям и методам решения и отличаются по размерности; размерность задачи построения расписания занятий в общем случае выше, чем значение этого параметра в задаче построения расписания экзаменов.
3. В результате системного анализа выявлены основные сущности Системы поддержки образовательного процесса: учебные группы, предметы, преподаватели, расписания сессий. Влияния различных факторов на студентов оценены на основе анкетного опроса, большое влияние на результаты оказывает уровень знаний преподавателей и организация учебного процесса.
4. Доказано путем проверки гипотез влияние последовательности экзаменов на их результаты.
5. Введены энтропийные оценки распределений оценок студентов на сессиях и доказано снижение энтропии при применении рациональной последовательности экзаменов.
Библиографическая ссылка
Аль-Габри В.М., Гранков М.В., Долятовский В.А. ЭНТРОПИЙНЫЙ АНАЛИЗ ДЛЯ ОЦЕНКИ ЭФФЕКТИВНОСТИ РАСПИСАНИЯ ЭКЗАМЕНОВ В ВУЗЕ // Фундаментальные исследования. – 2017. – № 11-1. – С. 9-14;URL: https://fundamental-research.ru/ru/article/view?id=41889 (дата обращения: 23.11.2024).