Исследованиям тентовых сооружений посвящено много работ отечественных и зарубежных авторов, особенно после знаменитых проектов Фрея Отто [1, 2]. В них приводятся классификации и анализ, отмечающие особую перспективность и в то же время наименьшую изученность сооружений шатрового типа. Авторы ранее уделили большое внимание исследованию исторически наиболее известных шатровых оболочек на круглом плане, форма которых может быть описана вращением некоторой кривой вокруг вертикальной оси. Наряду с ними, широко внедряются шатровые покрытия на квадратном опорном контуре. Их примеры показаны на рис. 1.
Формообразование таких шатров мало изучено, чем объясняются ошибки в проектировании, конструировании и раскрое. Внешне это проявляется в образовании морщин и складок, которые снижают эстетические характеристики и сокращают сроки службы сооружений вследствие неравномерности напряжений и деформаций.



Рис. 1. Примеры шатровых покрытий на квадратном плане
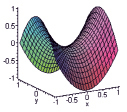

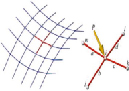
Рис. 2. Сетчатые модели тентовых оболочек
Цель исследования
Основной целью описываемых исследований является разработка научно обоснованной методики проектирования формы и расчета раскроя пленочно-тканевых заготовок для шатров на квадратном плане.
Так как форма таких оболочек представляет большую сложность для аналитического описания, были использованы численные методы моделирования и исследования. Для этого были разработаны и программно реализованы алгоритмы и математические модели:
- численного описания поверхности шатровой оболочки на квадратном плане;
- схемы границ и осей раскройных частей шатра, имеющих необходимую для тентов седловидную форму с отрицательной гауссовой кривизной;
- построения кратчайших линий на поверхности шатра на квадратном плане.
Численное моделирование формы шатровой оболочки
Авторами применен опубликованный ранее подход, основанный на конечно-разностном выражении (1), связывающем ординаты смежных узлов специального вида сетевых моделей тканевых оболочек.
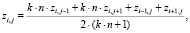 (1)
(1)
здесь 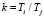 – соотношение усилий в нитях двух направлений,
– соотношение усилий в нитях двух направлений,
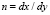 – соотношение шагов нитей двух направлений.
– соотношение шагов нитей двух направлений.
Особенность сетей в том, что их проекция на горизонтальную плоскость представляет собой ортогональную координатную систему. Примеры такого моделирования сетью показаны на рис. 2.
Допуская для пологих оболочек, что n = 1 и k = 1, приведенное выражение (1) упрощается и получает вид
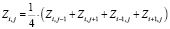 . (2)
. (2)
Оставляя постоянными значения ординат Z на контуре и в точках подвески оболочки, после ряда итераций можно получить сетчатую модель криволинейной формы поверхности оболочки. Степень ее гладкости зависит от шага нитей координатной сети и заданной точности вычисления ординат. Как показали экспериментальные расчеты, высокая для строительных сооружений точность определения ординат порядка 0,02 мм достигается уже при 50 итерациях.
Схема разбивки шатра на составные части для раскроя
Целесообразность разбивки шатров на ряд седловых поверхностей оправдана при использовании сетей Чебышева [3] для получения плоского раскроя шатра. Такой подход теоретически обоснован и экспериментально подтвержден авторами на примере оболочек вращения [4]. С применением этого методологического подхода, была разработана схема разбивки квадратных шатров на участки двух типов криволинейных элементов (ромбических – «клиньев» и треугольных – «вставок»), как показано на рис. 3.
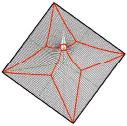
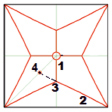
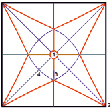
Рис. 3. Общий вид, схемы разбивки шатра и расположения осей раскроя
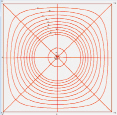
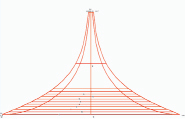
Рис. 4. Форма параллелей и горизонтальных сечений шатра на квадратном плане
Границы этих участков по конструктивным и технологическим требованиям должны являться кратчайшими (геодезическими) линиями, соединяющими характерные точки на поверхности оболочки. Предварительным анализом выявлено, что оптимальными с позиции раскроя характерными точками для построения границ являются указанные на рис. 3: осевые точки в подвеске шатра – т. 1, угловые точки опорного контура – т. 2, точки на диагональных сечениях шатра, расстояние до которых от центра основания шатра минимально – т. 4. Каждый участок представляет собой единый раскройный элемент. Для расчета карт их плоского раскроя необходимо построение осевых линий ориентации пленочно-тканевого материала оболочки на шатре. Осевые линии также должны являться геодезическими на поверхности. Их оптимальное положение показано на рис. 3 на правой схеме. Заметим, что все линии, совпадающие c меридиональными сечениями, являются кратчайшими по определению. Сложность представляет линия общего положения, соединяющая точки 2, 3 и 4. Способ ее построения представлен ниже.
Построение геодезической линии общего положения на поверхности шатра
За теоретическую основу метода принята теорема Клеро «О кратчайших линиях на поверхностях вращения», описанная в работе [5].
Исследуемый шатер на квадратном плане не является поверхностью вращения. Тем не менее его геометрия имеет некоторую топологическую схожесть с круговыми шатрами. Это видно на примере формы параллелей (горизонтальных сечений) квадратного шатра, представленной на рис. 4. В связи с этим сделана попытка распространить известные соотношения Клеро для направления кратчайшей на поверхности прямоугольных шатров. Основная сложность расчета в определении на поверхности направлений меридиана и кратчайшей, синус угла между которыми входит в формулу
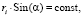
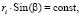 (3)
(3)
здесь ri – радиус параллели, α и β – углы кратчайшей с меридианом и параллелью. Для упрощения предлагается численный метод, основанный на определении координат некоторых вспомогательных точек на поверхности шатра. При этом потребовалось применить точный способ вычисления ординат произвольных точек на поверхности по координатам их горизонтальных проекций.
Алгоритмы вычисления ординат точек поверхности
Ниже представлены два интерполяционных алгоритма: линейный и параболический. Первый очень простой, но не достаточно точен для криволинейных поверхностей. Он принимает модель оболочки многогранником и удобен при малом шаге нитей сети. Соотношения (4) реализуют линейную интерполяцию.
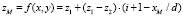 , (4)
, (4)
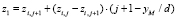 ,
,
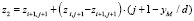 ,
,
где d – шаг сети; xM и yM – координаты проекции точки M на плоскость XOY.
Второй, параболический, более точен, так как учитывает кривизну поверхности, как показано на рис. 5. При параболической интерполяции искомые значения ординат вычисляются по многочленам второй степени (5). В (5а) приводятся формулы для расчета коэффициентов Ki многочленов по направлению нитей вдоль координатной оси ОХ. Аналогично проводится расчет по оси OY. Как видно на правой схеме рис. 5, для вычисления требуются координаты девяти смежных узлов. На схеме они обозначены номерами от 1 до 9.
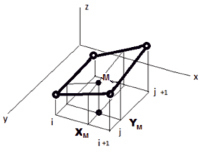
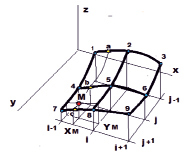
Рис. 5. Схемы линейной (слева) и параболической (справа) интерполяции при вычислении координат точек на криволинейной поверхности мягких оболочек
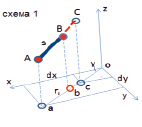
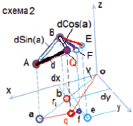
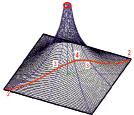
Рис. 6. Схемы и пример построения геодезической линии на шатре
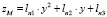 , (5)
, (5)
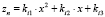 ,
,
при
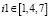 ;
; 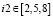 ;
; 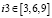
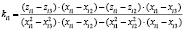 , (5а)
, (5а)
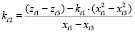 ,
,
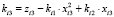 .
.
Коэффициенты 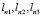 вычисляются аналогично
вычисляются аналогично 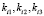 с заменой координаты xi на yn и Zi на Zn, где
с заменой координаты xi на yn и Zi на Zn, где 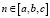 .
.
Вычисление координат узлов геодезической на поверхности
Для расчета искомая линия моделируется ломаной из прямолинейных отрезков малой длины. Предлагаемый способ вычисления координат ее узлов иллюстрируют схемы на рис. 6.
Схема 1 поясняет способ вычисления координат некоторой точки «В» на поверхности шатра, отстоящей от известной точки «А» на расстоянии «S», в направлении, заданном азимутом «γ» на горизонтальной плоскости. Последовательность решения следующая:
1) по формуле (6а) отыскивается проекция т. С отрезка «а-с» длиной S;
2) вычисляется ордината Zc по соотношениям (5);
3) рассчитывается длина отрезка А-С на поверхности по выражению (6б);
4) определяются координаты т. В по (6в), а затем (5) для отрезка AB длиной S.
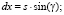
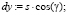 (6а)
(6а)
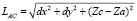 ; (6б)
; (6б)
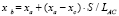 ,
,
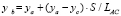 . (6в)
. (6в)
Если принять длину отрезка АВ равной 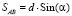 , где d – длина малого участка геодезической линии, тогда отрезок AB будет проекцией участка кратчайшей на меридиан. Для определения положения искомого участка можно использовать описанный алгоритмом для поиска его проекции на параллель.
, где d – длина малого участка геодезической линии, тогда отрезок AB будет проекцией участка кратчайшей на меридиан. Для определения положения искомого участка можно использовать описанный алгоритмом для поиска его проекции на параллель.
Это отрезок BF, перпендикулярный А-В и длиной 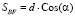 , как показано на схеме 2 рис. 6. Отрезок AF является первым приближением искомого участка кратчайшей. Необходимо провести интерполяционное уточнение его длины по формулам (6) и (5). В результате интерполяции определится положение узла Q на поверхности шатра, для которого выполняются требования (7).
, как показано на схеме 2 рис. 6. Отрезок AF является первым приближением искомого участка кратчайшей. Необходимо провести интерполяционное уточнение его длины по формулам (6) и (5). В результате интерполяции определится положение узла Q на поверхности шатра, для которого выполняются требования (7).
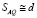 ,
, 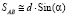 ,
, 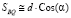 . (7)
. (7)
Пример геодезической линии на поверхности шатра, построенной описанным алгоритмом, приведен на рис. 6 справа.
Радиусом параллели для следующего узла является длина луча 0-q. Это позволяет вычислить, в соответствии с (3), синус угла для определения направления следующего участка кратчайшей
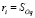 ,
, 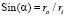 , (8)
, (8)
ro – в т. 4, конечном узле кратчайшей линии.
Здесь ro – радиус параллели в конечной точке кратчайшей (т. 4 на рис. 6).
Выводы
Результаты экспериментальных расчетов, графически представленные на рис. 3, подтверждают возможность использования предлагаемых алгоритмов и формул для вычисления координат узлов геодезических линий на поверхности квадратного шатра, с целью оптимизации его раскроя.
Библиографическая ссылка
Кудрявцева В.И., Удлер Е.М. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ГЕОМЕТРИИ ТЕНТОВЫХ ШАТРОВ НА ЖЕСТКОМ КВАДРАТНОМ КОНТУРЕ // Фундаментальные исследования. 2017. № 10-3. С. 466-470;URL: https://fundamental-research.ru/ru/article/view?id=41859 (дата обращения: 17.11.2025).



