Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ембулаев В.Н. 1 Тонких А.И. 2

---

1 Владивостокский государственный университет экономики и сервиса

2 Дальневосточный федеральный университет

Организационная структура управления угольной промышленностью на уровне региона представляет собой трёхуровневую (многоуровневую) иерархическую структуру, в которой общую задачу управления можно представить как состоящую из нескольких «элементарных» двухуровневых подсистем. Математическое описание задачи взаимодействия между элементами в многоуровневой иерархической структуре основано на обобщении полученных результатов для двухуровневых подсистем. В каждой двухуровневой подсистеме на верхнем уровне имеется один элемент, который связан с несколькими элементами на нижнем уровне. Взаимодействие между элементами происходит по следующей схеме: для каждого элемента на нижнем уровне конструируется задача векторной оптимизации и решение, оптимальное для всей подсистемы, ищется в пределах эффективного множества (множества Парето) значений этой задачи. На основе этой процедуры взаимодействия между элементами в целях поиска оптимального решения были разработаны безытеративный (однократный обмен информацией между уровнями) и итеративный (многократный обмен информацией между уровнями) алгоритмы координации.

Статья в формате PDF

0 KB

угольная промышленность

регион

управление

иерархическая многоуровневая структура

взаимодействие элементов.

1. Яновский А.И. О состоянии и мерах по развитию угольной промышленности России // Уголь. – 2010. – № 8. – С. 3–11.

2. Ембулаев В.Н., Тонких А.И. Совершенствование управления предприятиями угольной промышленности в целях повышения конкурентоспособности: монография. – Владивосток: Изд-во «Дальнаука», 2010. – 243 с.

3. Ембулаев В.Н., Тонких А.И. Математическое описание задачи управления в угольной промышленности // Вестник ТОГУ. – 2011. – № 2 (21). – С. 129–138.

4. Johannes J. Vector Optimization: Theory, Applications, and Extensions. Berlin, Heidelberg, New York: Springer-Verlag, 2010. – 460 p.

5. Yu. K. Mashunin, K. Yu. Mashunin. Simulation and Optimal Decision Making the Design of Technical Systems (2. The decision with a criterion priority) // American Journal of Modeling and Optimization. – 2016. – Vol. 4. № 2. – Р. 51–66.

6. Hirotaka N., Yeboon Y., Min Y. Sequential Approximate Multiobjective Optimization Using Computational Intelligence. Berlin, Heidelberg: Springer-Verlag, 2009. 197 p.

7. Ansari Q., and Jen-Chih Y. Recent Developments in Vector Optimization. Heidelberg, Dordrecht, London, New York: Springer, 2010. – 550 p.

В состав Дальневосточного экономического региона входят 9 субъектов Федерации: Республика Саха, Приморский, Хабаровский и Камчатский края, Амурская, Магаданская и Сахалинская области, Еврейская автономная область и Чукотский автономный округ. В каждом из них имеется несколько угольных месторождений. Например, в Приморском крае имеется 6 угольных месторождений: Бикино-Уссурийское, Ханкайское, Угловское, Партизанское, Раздольненское. На каждом угольном месторождении имеется несколько шахт и разрезов. Например, на Раздольненском месторождении имеются следующие шахты и разрезы: Липовецкий, Ильичёвский, Константиновский, Уссурийский и Алексее-Никольский [1, 2].

Следовательно, объект управления угольной промышленностью на уровне региона можно представить в виде трёхуровневой иерархической структуры (см. рисунок): регион – субъекты Федерации – угольные месторождения. В свою очередь и субъект управления тоже может быть представлен в виде трёхуровневой иерархической структуры: регион (1-й уровень) управляет субъектами Федерации, субъект Федерации (2-й уровень) управляет угольными месторождениями, которые (3-й уровень) управляют шахтами и разрезами.

Такое описание объекта и субъекта управления в угольной промышленности на уровне региона позволяет рассматривать данную трёхуровневую иерархическую структуру управления как бы состоящую из конечного числа двухуровневых подсистем, в которых на верхнем уровне (на первом и втором уровнях) имеются по одному элементу, а на соответственно нижнем уровне (на втором и третьем уровнях) имеется по несколько элементов, причём каждый из них связан с одним и только с одним элементом на верхнем уровне. Это означает, что общая задача управления в угольной промышленности на уровне региона разбивается на ряд локальных (двухуровневых) подзадач, решаемых соответствующими органами управления. В работе [3] была рассмотрена постановка задачи управления в системе с двухуровневой иерархической структурой и разработаны итеративные и безытеративные алгоритмы координации в таких системах. Теперь попытаемся обобщить полученные результаты и для иерархических систем, в которых имеется больше чем два уровня (на примере региона с трёхуровневой иерархической структурой).

Представленная на рисунке иерархическая структура имеет К = 3 уровня, на каждом из которых содержится по Nk элементов, где 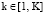(N1 = 1, N2 = 5, N3 = 11). Каждый элемент k-го уровня, начиная со второго, связан с одним и только с одним элементом вышестоящего уровня. Это позволяет ввести обозначение множества 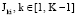, соответствующее множеству индексов элементов (k + 1)-го уровня, относящихся к элементу (k, i) – i-й элемент k-го уровня. (На рисунке имеем, что 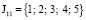, , 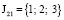J22 = {4; 5}, J23 = {6; 7}, J24 = {8}, J25 = {9; 10; 11}).

Для множества Jki справедливы свойства:

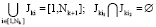
при .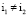

Далее будем считать, что состояние элемента (k, i) характеризуется вектором xki, где 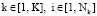, передаваемые на верхний уровень показатели этого элемента обозначаются вектором 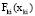, а 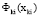является векторным критерием элемента.

Взаимосвязь между элементами на разных уровнях задаётся следующим соотношением:

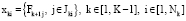, (1)

(на рисунке 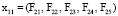, 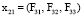и т.д.). Согласно введённым обозначениям, состояние элемента (k, i) определяется совокупным вектором показателей элементов (k + 1)-го уровня, относящихся к элементу (k, i).

Укажем ограничения, которым должны удовлетворять векторы xki.

Для K-го (самого нижнего) уровня ограничения записываются в виде

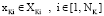, (2)

где XKi – некоторые множества.

Векторы xki, где 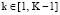, должны удовлетворять ограничениям

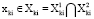, (3)

где

; ,

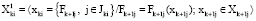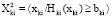где Hki – вектор функции; bki – векторы.

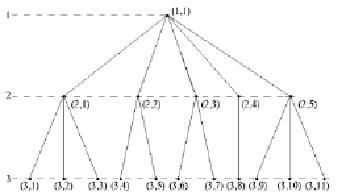
Система элементов трёхуровневой иерархической структуры

Так, например, для элемента при k = 2 и i = 1 имеем: ;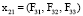

;

.

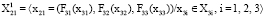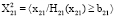В связи с совпадением целевых функций системы и элемента первого уровня их можно записать как

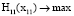. (4)

Данные теоретические изложения показывают, что формализация задачи управления в системе с многоуровневой иерархической структурой является задача (1)–(4). А в работе [4] показано, что такие задачи имеют решение в виде

.

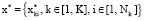Для решения данной задачи, аналогично, как и для двухуровневых иерархических систем, введём следующее предположение: для элементов всех уровней, начиная со второго, выполняются условия

,

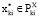где 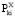– множество Парето задачи векторной оптимизации

, , , ,

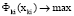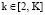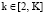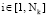где Фki – векторный критерий элемента (k, i).

Чтобы вводимое предположение выполнялось достаточно задать условия в виде следующего утверждения: пусть для функций Нki и Fki выполняются следующие условия монотонности:

1) ;

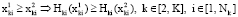2) ;

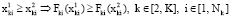3) .

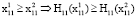И если положить, что

,

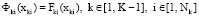то этого вполне достаточно, чтобы убедиться в справедливости вводимого предположения, т.е. вектор показателей выбрать в качестве векторного критерия элементов.

Если считать, что вводимое предположение не выполняется, то существует элемент 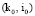(при доказательстве данного утверждения будем считать, что i0 = 1), для которого найдётся такая точка 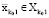, что 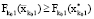. Но поскольку 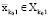, тогда найдутся элементы 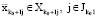, такие, что .

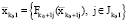И если теперь из точки 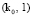опускаться вниз по пирамиде, то неизбежно обнаружим, что существуют допустимые векторы 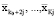, позволяющие достигнуть вектор .

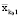При движении по пирамиде вверх от элемента (k0, 1) на вышестоящие уровни 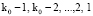, на каждом из них тоже будут элементы с первыми номерами в пределах своего уровня: 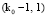, , 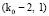...,(2, 1), (1, 1).

Рассмотрим точку

.

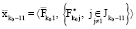Но поскольку 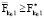, то из этого следует, что 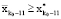. А из условий монотонности (см. утверждение) вытекает, что 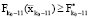и 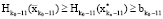. А это соответствует тому, что .

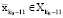Аналогичные рассуждения приводят к тому, что существует некоторая точка 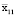, 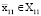и что выполняется 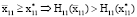. А это противоречит оптимальности точки .

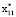В работе [3] осуществлена математическая постановка задачи управления в системе с двухуровневой иерархической структурой, и предложены безытеративный и итеративный алгоритмы координации в качестве решения данной задачи. При безытеративном алгоритме координации происходит однократный обмен информацией между уровнями. При итеративном алгоритме координации оптимальное решение определяется в ходе многократного обмена информацией между уровнями.

Теперь попытаемся обобщить эти методы решения и для задач управления в системах с многоуровневой иерархической структурой.

Безытеративный алгоритм координации. Для элементов самого нижнего K-го уровня вводятся в рассмотрение задачи векторной оптимизации

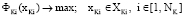. (5)

Предположим, что вектор

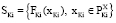
является вектором решения задачи. Подымаясь по пирамиде вверх на (K–1)-й уровень, передаётся множество QKi, которое является подмножеством множества SKi. В частности, может быть QKi = SKi.

Укажем несколько возможных вариантов задания множества QKi [4, 5].

1. Если множество XKi состоит из конечного числа точек, то подмножество QKi также состоит из конечного числа точек. При небольшом количестве точек QKi = SKi. В противном случае методами кластерного анализа производится «сжатие» информации, в результате чего передаваемое подмножество QKi будет содержать заданное число точек.

2. Задача векторной оптимизации (5) является задачей многокритериального линейного программирования, а показатели 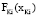также являются линейными функциями. Тогда в качестве подмножества QKi можно использовать линейную комбинацию эффективных крайних точек многогранника 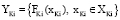[6].

3. В случае, когда задача (5) является нелинейной многокритериальной задачей, можно аппроксимировать множество SKi конечной ε-сетью или проводить многогранную аппроксимацию.

Для элементов на уровнях K–1, ...,3, 2 вводятся задачи векторной оптимизации:

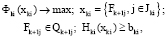
где

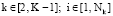. (6)

Решая эти задачи, формируют подмножества Qki, являющиеся аппроксимацией множеств .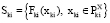

Рассмотрим несколько частных случаев задачи (6).

1. Пусть подмножества 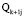состоят из конечного числа точек, а функции Фki и Hki являются линейными. Тогда задача (6) является задачей многокритериального целочисленного программирования:

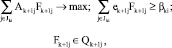
где 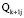– конечные множества, 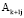– прямоугольная матрица, 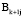– невырожденная подматрица (базис) матрицы (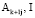), где I – квадратная единичная матрица [7].

2. Подмножества 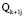являются многогранниками, заданными своими вершинами 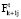, где .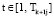

По-прежнему считая функции Фki и Нki линейными, получим задачу многокритериального линейного программирования:

.

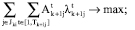
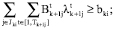
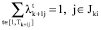Подымаясь по пирамиде вверх и оказавшись на самом верхнем, первом уровне, решается обычная задача математического программирования:

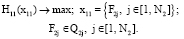
Итеративный алгоритм координации. На примере многоуровневой иерархической системы, приведённой на рисунке, покажем схему итеративного алгоритма координации. Пусть 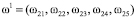– вырабатываемый элементом самого верхнего, первого уровня координирующий сигнал, который посылается элементам второго уровня. После получения элементом (2, i), i∈[1, 5] координирующего сигнала ω_2i, условием оптимальности функционирования можно представить в виде следующей задачи:

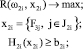
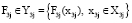. (7)

Заметим, что задача (7) является рассмотренной в работе [3] задачей координации в двухуровневой системе, поэтому процедура решения заключается в том, что элементам третьего уровня координирующие сигналы формирует элемент (2, i). Эти координирующие сигналы позволяют осуществить свёртку многокритериальных задач элементов третьего уровня в задачи математического программирования:

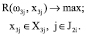(8)

На основе полученных результатов при решении задач (8) элемент (2, i) решает координирующую задачу и вырабатывает новые координирующие сигналы для элементов третьего уровня. В результате итеративного обмена информацией между элементом (2, i) и подчинёнными ему элементами третьего уровня определяется решение задачи (7), которое зависит от координирующего сигнала ω_2i.

Далее уже на самом первом уровне формируется и решается координирующая задача элемента, в результате чего появляется новое значение координирующего сигнала ω¹. Когда элементы (2, i) получат этот сигнал, то они начинают вновь решать задачи координации подчинённых им элементов из третьей группы. И этот процесс продолжается до тех пор, пока не будет найден оптимальный координирующий сигнал ω^1*.

В работе показана возможность применения известных алгоритмов решения задач координации для трёхуровневых систем, состоящих из конечного числа двухуровневых подсистем (элементов). В зависимости от задания множества значений, описывающих состояние элементов в трёхуровневой системе, задачи координации могут быть представлены в виде задач целочисленного, линейного и математического программирования. А для таких задач разработаны и широко применяются на практике эффективные методы решения. 

Библиографическая ссылка