Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шарапова В.М. 1 Шарапова Н.В. 1 Борисов И.А. 1

---

1 ФГБОУ ВО «Уральский государственный экономический университет»

В статье рассматривается модель линейного стимулирующего контракта. Актуальность данной темы подтверждается широким использованием линейного контракта на практике, особенно при формировании систем оплаты труда. Целью статьи является анализ модели линейного контракта и выявление ключевых факторов, определяющих его вид. В статье приводятся допущения и ключевые результаты модели. Описываются стратегии поведения участников контракта. Дается содержательная интерпретация составляющих оптимального контракта. Определяются свойства сравнительной статики в отношении отдельных составляющих контракта и его структуры. Делаются выводы в отношении факторов, определяющих соотношение переменной и постоянной части вознаграждения. Проводится сравнение с оптимальным контрактом при полной информации, выявляются мотивы принципала на установление переменной части вознаграждения. Оценивается эффективность модели с точки зрения создания стимулов для исполнения условий контракта.

Статья в формате PDF

0 KB

линейный контракт

асимметричная информация

принципал-агент

1. Bengt Holmstrom, Paul Milgrom. Aggregation and Linearity in the Provision of Intertemporal Incentives // Econometrica. – Mar., 1987. – Vol. 55, № 2. – Р. 303–328.

2. Chan David C. Teamwork and Moral Hazard: Evidence from the Emergency Department (2016). – URL: http://fsi.stanford.edu/sites/default/files/teamwork_and_moral_hazard.pdf.

3. Sarkisian R. Team Incentives under Moral and Altruistic Preferences: Which Team to Choose? (2016). – URL: https://editorialexpress.com/cgi-bin/conference/download.cgi?db_name=EEAESEM2017&paper_id=73.

4. Ёжикова Н.А., Вешкина Л.В. Проблемы разработки стимулирующих контрактов в условиях развитой рыночной экономики // Вестник Пермского национального исследовательского политехнического университета. Социально-экономические науки. – 2012. – № 17(43). – С. 73–83.

5. Миллер А.Е., Миллер М.А. Исследование трудовых отношений в контексте стимулирующего контракта //Нормирование и оплата труда в промышленности. – 2015. – № 8. – С. 11–17.

6. Колосова О.Г. Целевой подход к реализации эффективного контракта // Вестник Сургутского государственного университета. – 2016. – № 4(14). – С. 20–27.

7. Пантя Ю.М. История развития проблемы принципала-агента // Журнал экономической теории. – 2011. – № 4. – С. 212–215.

8. Тужик А.М., Шуленина Д.И., Зайцева Е.В. Экономика и современный менеджмент: теория и практика. – 2015. – № 54–55–2. – С. 102–108.

9. Schattler H., Sung J. The First-Order Approach to the Continuous-Time Principal-Agent Problem with Exponential Utility. / H. Schattler, J. Sung // Journal of Economic Theory. – 1993. – Vol. 61. – Р. 331–371.

10. Muller H. The First-Best Sharing Rule in the Continuous-Time Principal-Agent Model with Exponential Utility / Holger M. Muller // Working Paper Series in Economics and Finance, № 145, December 1996.

Линейный контракт наряду с пороговым является одной из наиболее применяемых на практике форм вознаграждения участников контракта о найме, в первую очередь в трудовых контрактах. Особенностью линейного контракта является то, что агент получает вознаграждение, состоящее из двух частей, постоянной и переменной, причем переменная часть линейно зависит от показателей производительности агента.

1. Наибольший вклад в разработку моделей линейного контракта внесли Б. Холмстрем и П. Милгром в свой всемирно известной работе 1987 г. [1]. Впоследствии в разное время этой проблеме уделяли внимание многие исследователи, среди которых можно упомянуть наиболее современные публикации D.C. Chan [2], R. Sarkisian [3] и др. В отечественной литературе данная проблема получила развитие в работах Н.А. Ёжиковой, Л.В. Вешкиной [4], А.Е. Миллера, М.А. Миллера [5], О.Г. Колосовой [6], Ю.М. Пантя [7], А.М. Тужик, Д.И. Шулениной, Е.В. Зайцевой [8] и др.

Рассмотрим основные результаты данного исследования.

Введем основные допущения модели.

Существует множество возможных результатов реализации контракта, которые являются случайными величинами с известным законом распределения. Агент может повлиять на вероятность достижения того или иного результата за счет предприятия определенных усилий. Предпринимаемые агентом усилия затратны, и эти затраты могут быть выражены в денежных единицах.

Функции полезности принципала и агента являются экспоненциальными с постоянным индексом неприятия риска (CARA):

Функция полезности принципала:

.

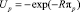Функция полезности агента:

.

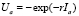Агент контролирует технологию, описываемую одномерным броуновским движением со сдвигом:

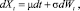
где Xt – информационный сигнал об усилиях агента, в роли которого выступает доход принципала, μ – уровень усилий агента, определяющий величину сдвига в броуновском движении (математическое ожидание дохода принципала, Wt – вайнеровский случайный процесс (одномерное броуновское движение). «За время dt приращение вайнеровского процесса dW – это нормально распределенная случайная величина со средним 0 и дисперсией dt» [1].

Продолжительность контракта фиксирована и нормализована к единице. Таким образом, в конце периода 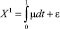, где ε нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией σ².

Принципал вознаграждает агента в конце контракта на основе известной траектории приращения дохода.

Согласно принятым допущениям задача принципала примет вид

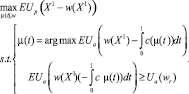(1)

Решая данную задачу, Б. Холмстрем и П. Милгром доказывают теорему, согласно которой в оптимуме агент будет прикладывать постоянный уровень усилий на протяжении всего контракта, а оптимальная величина вознаграждения будет линейно зависеть от сигнала об усилиях агента, измеренного по окончании срока контракта (то есть от X1) [1].

С использованием вывода о линейности оптимального вознаграждения задача принципала фактически сводится к статической, предполагающей выбор оптимального контракта из множества линейных, то есть фактически решается проблема, выбора вида функциональной формы контракта, которая была существенным ограничением однопериодных моделей скрытых действий.

Пусть теперь принципал выбирает вознаграждение, состоящее из постоянной части S и переменной части W = wX, где X – информационный сигнал, на основе которого формируется переменная часть вознаграждения (в данном случае – доход принципала), w – дополнительный бонус, получаемый агентом за улучшение информационного сигнала на единицу.

Таким образом, задача принципала с использованием свойства производящей функции моментов примет вид

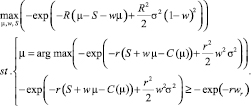(2)

Перейдем к решению задачи принципала.

Так как при решении задачи используется подход первого наилучшего, решим задачу агента.

При данной системе вознаграждения, необходимые условия максимизации ожидаемой полезности для агента примут вид

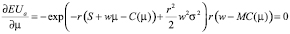. (3)

Отсюда получаем оптимальный уровень усилий агента: .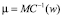

Что, например, для квадратичной функции издержек вида 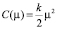дает: .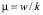

С использованием решения задачи агента лагранжиан для задачи принципала примет вид

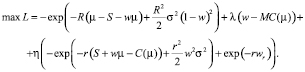(4)

Где η множитель Лагранжа при ограничении на участие.

Необходимые условия максимизации полезности примут вид

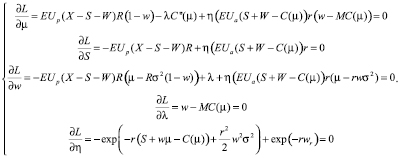(5)

Из производной Лагранжиана по постоянной части вознаграждения видно, что ограничение на участие должно выполняться как равенство.

Так как ограничение на участие выполняется как равенство, из него мы можем получить структуру постоянной части вознаграждения:

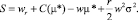(6)

То есть для заданного уровня усилий оптимальная структура вознаграждения примет вид:

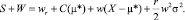(7)

Содержательная интерпретация структуры оптимального вознаграждения была дана в известно статье Ш. Шатлер и Дж. Сунг (1993) [9] и является общепринятой на сегодняшний день. Согласно их интерпретации компоненты вознаграждения играют следующую роль в оптимальном контракте:

• w_r – компенсация агенту альтернативных издержек заключения контракта;
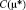•   – компенсация издержек предприятия предписываемых принципалом усилий;
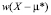•   – мотивация должных усилий и оптимальное распределение риска (содержит дополнительное вознаграждение, возникающая из-за того, что агент формирует мотивационную схему основываясь на ограниченной информации);
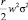•   – премия за риск (равна нулю для нейтрального к риску агента).

Решая систему уравнений, получаем уравнение, дающее оптимальный для принципала уровень усилий.

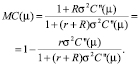(8)

Что, например, для функции издержек агента вида 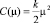дает следующее решение:

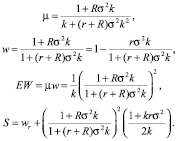(9)

Для оптимального контракта справедливы следующие свойства сравнительной статики.

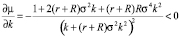, (10)

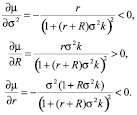(11)

То есть предписываемый принципалом уровень усилий тем выше, чем меньше издержки приложения усилий, чем меньше риск технологии, чем больше индекс неприятия риска принципала и чем меньше индекс неприятия риска агента.

Аналогичный результат получается для ставки переменной части вознаграждения и ожидаемой переменной части вознаграждения соответственно:

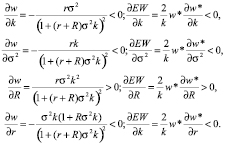(12)

Где w* оптимальный наклон переменной части вознаграждения, полученный в ходе решения задачи.

Сравнительная статика для постоянной части вознаграждения не позволяет получить однозначных результатов. С одной стороны, постоянная часть вознаграждения увеличивается с ростом предписываемого уровня усилий и переменной части за счет компенсации издержек приложения усилий и премии за риск, но, с другой стороны, постоянная часть может также снижаться за счет уменьшения на величину ожидаемой переменной части.

Более интересные результаты могут быть получены при анализе структуры вознаграждения, для чего воспользуемся соотношением между ожидаемой переменной частью вознаграждения и постоянной частью без учета резервной заработной платы.

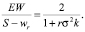(13)

Как видно, выражение имеет достаточно простой вид и легко поддается интерпретации. Доля переменной части вознаграждения будет расти с сокращением издержек приложения усилий, индекса неприятия риска агента и риска технологии. При этом особо следует отметить, что данное соотношение в модели Б. Холмстрема – П. Милгрома не зависит от индекса неприятия риска принципала.

Таким образом, по результатам анализа свойств сравнительной статики мы приходим к следующим результатам для постоянной части вознаграждения.

С ростом издержек приложения усилий, риска технологии и индекса неприятия риска агента, постоянная часть вознаграждения по крайней мере сокращается в меньшей степени, чем переменная.

С ростом индекса неприятия риска принципала происходит пропорциональный рост переменной и постоянной части.

С целью оценки влияния асимметрии информации на оптимальный контракт рассмотрим модель оптимального контракта в отсутствие асимметрии информации, предложенную Х. Мюллером (1996 г.) [10].

Мюллер в своей работе доказывает, что и в отсутствие асимметрии информации при сохранении остальных допущений модели Б. Холмстрема – П. Милгрома оптимальный контракт будет иметь линейнуюформу.

Следовательно, единственным отличием от предыдущей модели будет пассивная роль ограничения по стимулам, так как принципал, явно наблюдающий усилия агента, будет иметь возможность наложить на него бесконечный штраф в случае уклонения от предписываемого уровня.

Таким образом, задача принципала примет вид

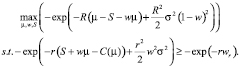(14)

Функция Лагранжа для задачи принципала примет вид

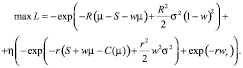(15)

Где η множитель Лагранжа при ограничении на участие.

Необходимые условия максимизации полезности примут вид

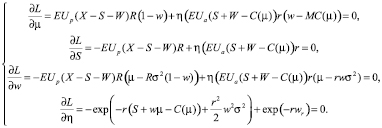(16)

Так же как и в предыдущей модели, активная роль ограничения на участие позволяет нам прийти к аналогичной структуре вознаграждения агента, допускающей аналогичную интерпретацию:

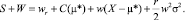(17)

Решая систему уравнений, получаем уравнение, дающее оптимальный для принципала уровень усилий .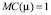

Что, например, для функции издержек агента вида 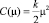дает следующее решение: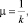

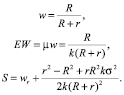(18)

Для оптимального контракта справедливы следующие свойства сравнительной статики:

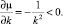(19)

То есть предписываемый принципалом уровень усилий тем выше, чем меньше издержки приложения усилий, и не зависит от предпочтений принципала и агента и риска технологии.

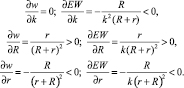(20)

То есть ставка переменной части однозначно определяется предпочтениями принципала и агента и тем больше, чем больше индекс неприятия риска принципала и меньше индекс неприятия риска агента. В отличие от предыдущей модели ненулевой наклон вознаграждения в данной модели объясняется только мотивом распределения риска. Для случая нейтрального к риску принципала агенту выплачивается фиксированное вознаграждение.

В отличие от предыдущей модели, мы можем получить достаточно определенные свойства сравнительной статики для некоторых аргументов постоянной части вознаграждения. Так можно утверждать, что постоянная часть вознаграждения возрастает с ростом риска технологии и сокращением издержек приложения усилий:

,

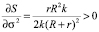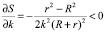. (1)

Для остальных аргументов нет однозначного влияния.

При этом в отличие от предыдущей модели соотношение между ожидаемой переменной частью и постоянной частью без резервной заработной платы зависит от индекса неприятия риска принципала:

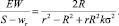(22)

Доля переменной части в вознаграждении сокращается с ростом индекса неприятия риска агента, издержек приложения усилий и риска технологии. Следовательно, приходим к выводу, что с ростом индекса неприятия риска агента, постоянная часть вознаграждения, по крайней мере, сокращается в меньшей степени, чем переменная, что аналогично случаю с асимметричной информацией.

Влияние индекса неприятия риска принципала оказывается неопределенным.

Библиографическая ссылка