Одним из основных направлений развития современного ткацкого оборудования является применение индивидуальных приводов исполнительных механизмов. Применение современных серводвигателей дает возможность совершенствования технологического оборудования в направлении упрощения конструкции, повышения надежности, снижения энергозатрат и повышения производительности.
В работе [1] предлагается модернизация механизма прокладки утка за счет применения индивидуального сервопривода, а также использования специального закона движения для данного механизма.
В любой конструкции, содержащей податливые элементы, например зубчатый ремень, валы, при возвратно-вращательном законе движения со скоростями, достигающими 400…450 об/мин, возможно возникновение колебательных явлений и упругих деформаций, которые способны вызвать нарушение требуемых технологических параметров работы технической системы. Поэтому необходима оценка упругих деформаций элементов в режиме вынужденных колебаний.
В этой связи целью данной работы является проверка работоспособности модернизированного механизма прокладки утка лентоткацкого станка ТЛА-2/70-С, заключающаяся в исследовании вынужденных крутильных колебаний механизма, деформаций элементов в конструкции и влиянии их на его работоспособность.
Для достижения поставленной цели в работе в качестве объекта исследования примем динамическую модель, разработанную для анализа собственных колебаний данного механизма [2].
Вынужденные колебания системы обусловлены силовым возмущением, согласно которому вращение диска J1 происходит по заданному закону движения, определяемому параметрами сервопривода, что отражено в динамической модели (рис. 1) в виде функции крутящего момента M(t), приложенного к диску J1.
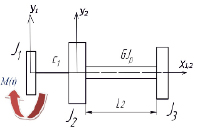
Рис. 1. Динамическая модель
На рисунке приняты следующие обозначения:
J1, J2, J3 – моменты инерции дисков; c1 – коэффициент жесткости на кручение; G – модуль сдвига; Jρ2 – полярный момент инерции поперечного сечения вала, L2 – длина вала.
Представим функцию вращающего момента M(t) в виде ряда Фурье [3].
Зависимость M(t), в нашем случае использования закона синусоидального ускорения [4], записывается следующим образом:
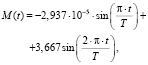 (1)
(1)
где T – период одного колебания, T = 0,15 с; 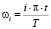 – гармоника разложения ряда Фурье, i – номер гармоники, i = 1, 2.
– гармоника разложения ряда Фурье, i – номер гармоники, i = 1, 2.
На рис. 2 представлены исходная функция R(t), заданная в табличном виде, разработанная специально для данного механизма и реализуемая сервоприводом – красная кривая, и функция M(t), представляющая аппроксимацию функции R(t) в виде ряда Фурье – синяя кривая. Рисунок иллюстрирует высокую сходимость представленных функций.
Для принятой динамической модели математическая модель системы получена «прямым способом» [5], а уравнение движения системы может быть найдено в результате решения системы дифференциальных уравнений второго порядка в частных производных, записанных в виде
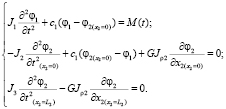 (2)
(2)
Представление крутящего момента в виде 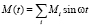 , позволяет получить решение системы (2) в замкнутой форме [6].
, позволяет получить решение системы (2) в замкнутой форме [6].
Решение уравнений системы (2) будем искать в виде возмущающей функции:
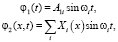 (3)
(3)
где φ1 – угол поворота диска J1, φ2 – угол закручивания произвольного сечения вала; A1 – амплитуда колебаний диска J1, Xi(x) – функция формы крутильных колебаний вала.
Подставляя (3) в (2), получим
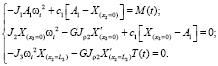 (4)
(4)
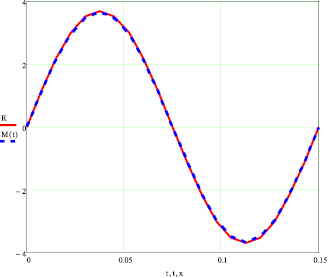
Рис. 2.
Функцию формы Xi(x), по технической теории крутильных колебаний стержней [6], определим в виде
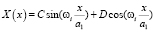
где C, D – неизвестные постоянные;
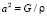 , ρ – плотность материала вала.
, ρ – плотность материала вала.
Для применения уравнения форм, для заданной схемы, необходимо записать граничные условия:
1) для сечения вала с координатой x2 = 0.
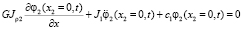 ,
,
2) для сечения вала с координатой x2 + L2.
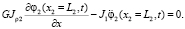
В итоге, учитывая граничные условия, получим
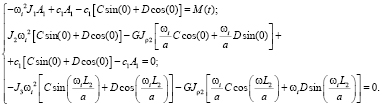 (5)
(5)
Для определения амплитуд вынужденных колебаний 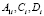 необходимо решить вытекающую из (5) систему уравнений в матричной форме:
необходимо решить вытекающую из (5) систему уравнений в матричной форме:
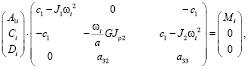 (6)
(6)
где
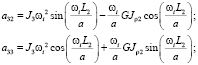
Значения искомых величин находим в виде (3)
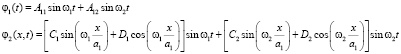 . (7)
. (7)
Для определения деформаций в значимых участках вала, а точнее в местах крепления дисков, следует вычесть из текущего угла поворота интересующего сечения вала угол поворота первого диска – принимаемого в виде ведущего звена, закон движения которого известен.
Угол закручивания диска
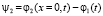 .
.
Угол закручивания диска
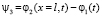 .
.
Абсолютная деформация вала
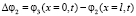 .
.
Для расчета принимаем следующие исходные данные [2]:
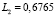 м,
м, 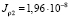 м4,
м4,
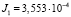 кг×м2,
кг×м2, 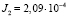 кг×м2,
кг×м2,
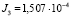 кг×м2,
кг×м2, 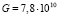 Н/м2,
Н/м2,
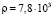 кг×м3, [τ] = 90МПа.
кг×м3, [τ] = 90МПа.
Как видно из графиков (рис. 3–5), деформации вала составляют: на диске ψ2 = 0,29 град, на диске ψ3 = 0,31 град, по длине вала Δφ2 = 0,02 град.
Вследствие наличия крутильных деформаций в сечениях валов возникает необходимость проверки валов по условию прочности, а зубчатого зацепления «звездочка – рейка» по условиям выполнения норм кинематической точности.
По закону Гука для касательных (сдвиговых) напряжений записывается выражение
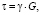 (8)
(8)
или в виде условия прочности для нашего случая
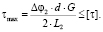 (9)
(9)
Подставляя исходные данные в (9) и сравнивая с расчетным значением:
0,4МПа ≤ 90МПа.
В результате определенное значение касательных напряжений показывает, что конструкция имеет достаточный запас прочности.
Кинематическая точность характеризуется разницей углов поворота сцепляющихся колес за один оборот. Нормы кинематической точности регламентируют полную погрешность передаточного числа, то есть наибольшую погрешность угла поворота для зубчатого колеса в пределах его оборота, для передачи за полный цикл изменений относительного положения зубчатых колес пары. Величины и характер кинематических погрешностей являются определяющими для зубчатой передачи.
В нормы кинематической точности входит параметр – допуск на накопленную погрешность шага по зубчатому колесу [7] (по ГОСТ 9178-81 и ГОСТ 1643-81), который может быть нарушен вследствие деформаций вала.
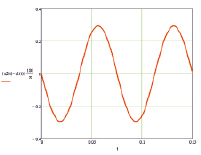
Рис. 3. Деформация вала в сечении под 2 диском, град
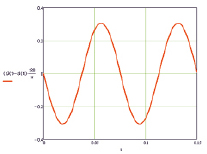
Рис. 4. Деформация вала в сечении под 2 диском, град
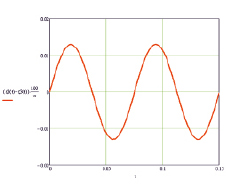
Рис. 5. Абсолютная деформация вала, град
В связи с тем, что зубчатая рейка челнока в какой-то момент движения находится в зацеплении одновременно с двумя соседними звездочками, деформации валов могут привести к нарушению геометрии зацепления.
Примем значение максимальной угловой деформации сечения вала в месте крепления звездочек, то есть Δφ2 = 0,02 град.
Тогда линейное смещение зуба будет равно
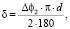 (10)
(10)
где Δφ2 – угловая деформация сечения вала в месте крепления звездочек, град;
d – делительный диаметр звездочки, м,
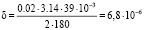 м или 6,8 мкм.
м или 6,8 мкм.
В нашем случае для 7-ой степени точности изготовления звездочки накопленная погрешность шага зацепления составляет δ = 42 мкм [7].
То есть упругие колебания валов вызывают величину погрешности шага зацепления на порядок меньшую, чем допускаемая точность изготовления, что должно обеспечить надежную работу зацепления.
Выводы
1. В соответствии с принятой динамической моделью механизма предложена математическая модель и решена задача о вынужденных крутильных колебаниях механизма.
2. Установлено, что при предложенном законе движения конструкция имеет достаточный запас прочности.
3. Существенных нарушений технологического процесса перемещения челнока в связи с колебаниями звеньев механизма не происходит.
Библиографическая ссылка
Пирогов Д.А., Шляпугин Р.В., Селезнев С.В. ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ ОСНОВНЫХ КОНСТРУКТИВНЫХ ЭЛЕМЕНТОВ МЕХАНИЗМА ПРИВОДА ЧЕЛНОКОВ ЛЕНТОТКАЦКОГО СТАНКА // Фундаментальные исследования. 2017. № 10-1. С. 34-39;URL: https://fundamental-research.ru/ru/article/view?id=41785 (дата обращения: 22.02.2026).



