Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Наумова Н.А. 1 Домбровский А.Н. 1 Данович Л.М. 1

---

1 ФГБОУ ВО «Кубанский государственный технологический университет»

Координация работы светофоров позволяет добиться безостановочного движения по магистрали для группы автомобилей и свести для них задержки к минимуму. Существуют различные технологические программы, реализующие алгоритмы управления дорожным движением. Актуальной задачей является определение условий координации работы светофоров в динамическом режиме. Развитие и внедрение Интеллектуальных транспортных систем позволяет получать, обрабатывать и выдавать полученные результаты в режиме реального времени. Авторская математическая модель распределения транспортных потоков по сети позволяет в динамическом режиме решать транспортные задачи. В работе представлен метод управления светофорной сигнализацией в условиях функциoнирования интеллектуальных транспортных систем. Приведен алгоритм определения оптимальных параметров светофорного регулирования по динамически обновляемым исходным данным авторской модели. Приведен алгоритм определения длины ленты безостановочного движения и величины оптимального сдвига фазы светофорного регулирования.

Статья в формате PDF

0 KB

светофорная сигнализация

Интеллектуальные транспортные системы

«зеленая волна»

математическая модель

1. Иносэ Х. Управление дорожным движением: Пер. с англ. / Х. Иносэ, Т. Хамада. – М.: Транспорт, 1983. – 248 с.

2. Gordon R.L., Warren P.E., Tighe P.E. Traffic Control Systems Handbook. Report No. FHWA-HOP-06-006. U.S. Department of Transportation Federal Highway Administration, October 2009. – 367 p.

3. Qing He. Robust-intelligent traffic signal control within a vehicle-to-infrastructure and vehicle-to-vehicle communication environment. UMI Number: 3423754. The University of Arizona, 2010. – 254 p.

4. Gordon R.L. Systems Engineering Processes for Developing Traffic Signal Systems. NCHRP Synthesis 307, Transportation Research Board, Washington, DC, 2008. – 367 p.

5. Naumova N.A. Method for Estimating An Origin-Destination Matrix for Dynamic Assignment // International Journal of Control Theory and Applications. – 2016. – Vol. 9 (30). – Р. 129–138.

6. Жанказиев С.В. Научные основы и методология формирования интеллектуальных транспортных систем в автомобильно-дорожных комплексах городов и регионов: дис. … докт. техн. наук: 05.22.01 / С.В. Жанказиев. – М., 2012. – 450 с.

7. Наумова Н.А. Выбор оптимальных параметров светофорного регулирования в узловой точке, при справедливости гипотезы о распределении интервалов по времени, по обобщенному закону Эрланга / Н.А. Наумова, К.А. Кирий, Т.А. Карачанская // Современные проблемы науки и образования. – 2013. – № 6.

8. Наумова Н.А. Теоретические основы и методы автоматизированного управления транспортными потоками средствами мезоскопического моделирования: дис. … докт. техн. наук: 05.22.10 / Н.А. Наумова. – Волгоград., 2015. – 331 с.

При высокой интенсивности движения автотранспортных средств и небольших расстояниях между соседними перекрестками, очередь, возникшая у одного перекрестка, может блокировать соседний. Снизить вероятность такой ситуации возможно путем организации «ленты безостановочного движения» или «зеленой волны» благодаря синхронизации работы светофоров [1]. Координация работы светофоров позволяет добиться безостановочного движения по магистрали для группы автомобилей и свести для них задержки к минимуму. Существуют различные технологические программы, реализующие алгоритмы управления дорожным движением, в том числе диспетчерское управление дорожным движением и организация «зеленой улицы» для специального транспорта [2]. Наиболее известная и широко применяемая в США и Европе программа, позволяющая координировать светофорную сигнализацию – TRANSYT [3]. Она была разработана в 1968 г. Робертсоном в Британской транспортной и дорожной научно-исследовательской лаборатории (TRRL). Кроме этого подобную транспортную проблему решают Synchro, PASSER, aaSIDRA, SCOOT, SCATS [4].

В условиях быстро меняющейся дорожной ситуации актуальной задачей является определение условий координации работы светофоров в динамическом режиме. Развитие компьютерных технологий, введение автоматизированных систем управления дорожным движением, внедрение Интеллектуальных транспортных систем позволяет получать, обрабатывать и выдавать полученные результаты в режиме on-line.

Мезоскопическая модель TIMeR_Mod, разработанная авторами [5], дает возможность решать как задачи, требующие выдачи результатов в режиме реального времени (что особенно важно для Интеллектуальных транспортных систем, так как позволяет динамично информировать участников дорожного движения), так и прогнозные задачи. И позволяет координировать режимы работы светофорной сигнализации с целью создания ленты безостановочного движения с учетом изменяющейся дорожной ситуации в режиме реального времени.

Определение оптимальной длительности цикла регулирования в динамическом режиме

В разработанной авторами модели TIMeR_Mod учитываются многополосные пересечения нерегулируемых перекрестков и перекрестков с жестким светофорным регулированием, разработаны соответствующие методы мониторинга, хранения и извлечения соответствующей информации. В работе [5] приведены результаты исследования авторов по обновлению в режиме on-line информации о состоянии и распределении транспортных потоков по сети, необходимой для функционирования модели TIMeR_Mod. А основной целью развития ИТС в области управления дорожным движением как раз и является возможность оперативного решения проблем снижения числа транспортных заторов, вероятности их возникновения, получение динамической информации о наиболее эффективных маршрутах, получение возможности в режиме реального времени рассчитывать оптимальные режимы светофорного регулирования на перекрестке [6]. Для закладки модели TIMeR_Mod в автоматизированные системы управления дорожным движением (АСУДД) необходимо комплексное решение проблемы, то есть разработка соответствующих методов мониторинга, хранения и извлечения необходимой информации при решении конкретных задач по оптимизации распределения транспортных потоков по сети.

В модели TIMeR_Mod улично-дорожная сеть (УДС) представлена связанными матрицами ASTREETS и BINTERSECTION. Строка матрицы ASTREETS содержит информацию об узловой точке, образованной пересечениями улиц S1 и S2 , и о перегоне между узловыми точкам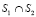и и :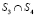

.

Строка матрицы BINTERSECTION содержит информацию о входящих и исходящих транспортных потоках для точки :

.

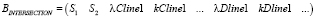Методы обновления информации в вышеуказанных матрицах по данным мониторинга улично-дорожной сети приведены в работе [5]. При определении оптимальной длительности цикла регулирования в динамическом режиме с помощью авторской модели TIMeR_Mod следует действовать по приведенному ниже алгоритму.

1. Работа по установлению ленты безостановочного движения начинается с определения маршрута. Формируем его как последовательность перекрестков. Составляем последовательность регулируемых перекрестков 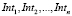. Информация о наличии или отсутствиии светофорного регулирования содержится в матрицах ASTREETS и BINTERSECTION.

2. По информации, содержащейся в матрице BINTERSECTION, выбираем наиболее загруженный регулируемый перекресток. Для этого среди перекрестков с наибольшей интенсивностью на одной из полос в магистральном направлении определяем «критический перекресток» – тот из них, у которого наблюдается наибольшая суммарная интенсивность.

3. Определяем оптимальные параметры для светофорного регулирования T, T1, T2. С этой целью используем методику, разработанную авторами и описанную, например, в работах [7, 8].

Пусть n1 – число потоков магистрали № 1; n2 – число потоков магистрали № 2;

h – среднее время (в секундах) между пересекающими узловую точку требованиями одного потока;

Hi(t) – функция восстановления для i-го потока магистрали № 1;

Wi(Ti, λ) – суммарная задержка всех требований i-го потока за один цикл регулирования;

Т1 – время, в течение которого запрещено движение для потоков магистрали № 1, с;

Т2 – время, в течение которого запрещено движение для потоков магистрали № 2, с;

T = T1 + T2.

Суммарная задержка всех транспортных средств данного потока за единицу времени – один час, выражается следующим образом:

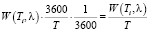(авт.•ч). (1)

Минимизировать требуется суммарную часовую задержку всех требований в данном узле. Целевая функция:

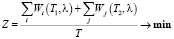. (2)

В результате следует получить оптимальные значения параметров регулирования T1, T2.

При этом для каждого потока должно выполняться условие отсутствия затора (то есть при движении требований по данной полосе количество требований, прибывающих к узловой точке за один цикл, не превышает количества требований, пересекающих ее за то время Ti, когда движение разрешено):

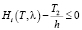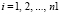, ; (3)

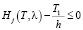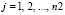, . (4)

Кроме этого необходимо выполнение условий:

25 ≤ T ≤ 120,

,

,

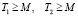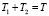где М – минимальное время (в секундах), необходимое требованию для пересечения узловой точки типа «регулируемое пересечение потоков требований».

Таким образом, получаем задачу математического (нелинейного) программирования (ЗМП):

;

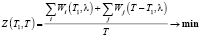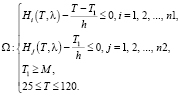
Целевая функция является функцией двух переменных, область Ω замкнутая. При условии, что область допустимых значений непустая, в работе [7] доказано существование решения данной задачи математического программирования.

Критические точки являются решением системы:

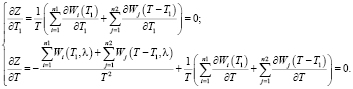(5)

В статье [7] разработан и описан алгоритм определения оптимальных значений T = Topt и T1 путем численного решения системы (5).

Если область Ω является пустой, то невозможно обеспечить ликвидацию очередей по всем направлениям. Тогда среди условий (3) и (4) оставляем условия для магистральной улицы, на которой требуется определить ленту безостановочного движения. После корректировки условий нахождение оптимальных параметров проводится по тому же алгоритму работы [7].

4. Принимаем на остальных перекрестках 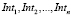длину цикла, равную Topt. По информации, содержащейся в матрицах ASTREETS и BINTERSECTION, определяем эффективную долю фаз регулирования.

Определение длины ленты безостановочного движения

Так называемая «зеленая волна» позволяет пропускать поток по магистральной улице без остановок у отдельных регулируемых перекрестков. В отличие от изолированных перекрестков, в этом случае светофорная сигнализация представляется и рассматривается как единая система. Чтобы поддержать безостановочный поток транспортных средств, система должна скоординировать режим работы светофоров на смежных перекрестках. С этой целью устанавливается сдвиг фаз как отношение интервала времени между серединами горения красных сигналов к длине цикла регулирования. Лента безостановочного движения определяется длительностью цикла регулирования, распределением периодов в рамках цикла и сдвигом.

Для определения длины ленты безостановочного движения и величины оптимального сдвига фазы светофорного регулирования будем использовать метод, обоснованнный в работе [1].

В формулах (6–8) используются следующие обозначения:

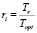– доля горения красного сигнала на перекрестке Inti;

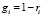– доля горения зеленого сигнала на перекрестке Inti;

γ_ij – относительный сдвиг (по модулю единицы) между перекрестками Inti и Intj, отношение интервала времени между серединами горения красных сигналов к величине Topt;

;

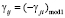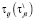( – отношение времени проезда в прямом (обратном) направлении от Si до Sj (без учета задержек) к длине цикла Topt;

uij – отношение интервала времени от конца периода горения красного сигнала светофора на Inti до момента времени, стартовав в который автомобиль достигнет Intj точно к концу горения красного сигнала, к длине цикла Topt;

Согласно [1]:

.

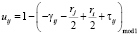Если учтено условие сбалансированности сдвигов, то отношение времени проезда в прямом направлении может быть рассчитано по следующей формуле:

,

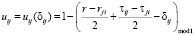где .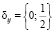

При расчете величины uij важна скорость движения потока транспортных средств. Этот факт в предлагаемой методике учитывается при расчете оптимального цикла и фаз светофорного регулирования. Функция восстановления Hi(T, λ) строится по текущим эмпирическим данным о величине интервалов по времени между автомобилями в потоке, тем самым учитывается в неявном виде скорость и состав потока транспортных средств.

Длина полосы безостановочного движения для Inti:

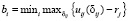. (6)

Длина оптимальной полосы безостановочного движения:

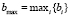. (7)

Пусть 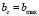. Тогда набор оптимальных сдвигов:

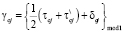. (8)

Величины 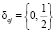выбирают из условия .

В работе Х. Иносэ и Т. Хамада математически строго обосновывается, что рассчитанная таким образом длина ленты безостановочного движения является оптимальной, то есть позволяет пропустить максимальное количество транспортных средств. Сдвиги фаз, определенные по формуле (8), являются сбалансированными.

Заключение

Проблема оптимального распределения транспортных потоков по сети в мировой практике в последние 40 лет решается с помощью внедрения Интеллектуальных транспортных систем. Перед ИТС последних поколений ставится задача принятия решений в режиме реального времени либо с краткосрочной задержкой реагирования. Основной причиной заторных ситуаций является неэффективная организация движения в узловых точках сети, как регулируемых, так и нерегулируемых.

В настоящее время для анализа и оптимизации движения транспортных потоков требуются инновационные инструменты, основанные на гибких математических моделях, которые позволяют достичь эффективного результата с учетом текущих изменений в режиме on-line. Представленное в работе решение задачи координации режимов светофорной сигнализации с целью формирования «зеленой волны» на данном маршруте не привлекает имитационное моделирование, проводится аналитическими методами, поэтому может быть использовано при автоматизированном управлении транспортными потоками в динамическом режиме. Данное новое решение известной задачи разработано специально для модели TIMeR_Mod.

Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект № 16-48-230720 р_а.

Библиографическая ссылка