В современном мире проблема измерения взаимосвязи между оценками населением своего уровня образования и субъективным представлением о благополучии является одной из основных при формировании надежной системы показателей, используемых для оценки непрерывного благополучия населения. Особенно остро этот вопрос стоит для людей пожилого возраста. Это связано с тем, что пожилые люди представляют в современном мире самую быстрорастущую возрастную группу. По оценкам ООН каждую секунду 2 человека достигают возраста 60 лет. В настоящее время пожилых – больше, чем детей до 5 лет, а к 2050 г. их количество превысит численность детей и подростков в возрасте до 15 лет [14]. По мировым меркам Россия относится к интенсивно стареющим сообществам: по данным за 1 квартал 2016 г. численность людей в возрасте выше трудоспособного составляет 24 % населения [6]. В Томской области в старшей возрастной группе находится каждый пятый житель, при этом доля лиц в возрасте старше 60 лет стабильно растет [4].
Оценка влияния уровня образования на благополучие граждан старшего поколения представляет особый интерес для Томской области, традиционно имеющей очень высокий образовательный статус населения в целом. Еще с советских лет область является одним из признанных российских лидеров по численности студентов вузов на 10 000 населения, уступая только федеральным городам. По данному показателю Томская область превышает средние по РФ значения более чем в полтора раза [7]. Доля населения с высшим образованием в Томской области составляет 32 %, что значительно превышает средний общероссийский показатель в 23 % [10].
Интерес исследователей к оценке взаимосвязи межу уровнем образования и субъективным представлением пожилых людей о своём благополучии вызван большим объемом статистических оценок и научных исследований в данной сфере, характерных как для ведущих стран ОЭСР [1], так и для России [15], а также для иных стран с догоняющей экономикой [11].
Исследования в данной области проводятся в основном на международном уровне, охватывая, как правило, большое количество государств, хотя статистические данные собираются также и по региональному принципу [8]. Для Российской Федерации в силу значительных различий в уровне жизни населения в целом и пожилых людей в частности чрезвычайно важен региональный аспект подобных исследований, позволяющий получать сопоставимые оценки для людей старших возрастных групп, проживающих в различных районах страны [3, 5, 9].
Изменение возрастной структуры современного общества, обусловленное неуклонным возрастанием доли пожилых людей в структуре населения, требует принципиальных изменений в социально-экономической политике, необходимости отражения в ней мер, ориентированных на удовлетворение особых потребностей людей старшего возраста. Новые социально-экономические решения, в том числе на региональном уровне, должны быть ориентированы на поддержку развития человека на протяжении всей его жизни, в том числе на создание условий для повышения благополучия пожилых людей.
Целью настоящей работы является установление характера и устойчивости связей между показателями, характеризующими уровень образования пенсионеров Томской области и субъективными оценками пожилыми людьми собственного благополучия. С учетом ограниченности фактической базы по параметрам благополучия пожилых людей в РФ, в том числе в региональном разрезе, сотрудниками Международной научно-образовательной лаборатории технологий улучшения благополучия пожилых людей, созданной при финансовой поддержке Министерства образования и науки Российской Федерации на базе Томского политехнического университета, было проведено специальное социологическое исследование.
Материалы и методы исследования
В ходе исследования было опрошено 400 пенсионеров Томской области, проживающих в пяти населенных пунктах и трех районах. Анкета включала 78 вопросов, отражающих социальные, экономические, психологические и физиологические характеристики пенсионеров. Список вопросов анкеты (с выбором только одного варианта индикатора), по которым проводится анализ данных, измеренных по ранговой шкале, представлен в табл. 1.
Таблица 1
Структура анкетных данных социологического опроса на примере образования
|
№ вопроса |
Вопрос |
Вариант ответа (уровень образования) |
Код ответа |
Ранг ответа |
|
№ 68 |
Какое у Вас образование? |
Имею ученую степень |
О1 |
1 |
|
Высшее |
О2 |
2 |
||
|
Среднее специальное |
О3 |
3 |
||
|
Среднее |
О4 |
4 |
||
|
Неполное среднее |
О5 |
5 |
Для исследования данных социологического обследования используются методы статистического анализа (дисперсионного, корреляционного, кластерного, факторного, регрессионного) [2, 13].
Следует заметить, что совокупность статистических характеристик и методов, которые могут быть применены для обработки анкетных данных, определяется однозначно типом измеряемой шкалы (номинальные, порядковые, интервальные).
Для номинальных (категориальных) переменных, характеризующих значения качественных признаков (пол людей, названия населенных пунктов, и т.п.), используются следующие статистические операции: расчет частот (удельных весов) объектов данной категории; определение моды изучаемого признака; применение различных методов статистического анализа, основанных на оперировании частотами (таблицами сопряженности), – критерия согласия Хи-квадрат для анализа связей между номинальными признаками и др. [12].
Для наиболее распространенных порядковых (ранговых) переменных, характеризующих возрастание или убывание степени проявления измеряемого свойства и допускающих ранжирование (упорядочивание) категорий объектов, используют ранговые (непараметрические) характеристики: медиану в качестве средней оценки, процент или в качестве меры рассеяния, ранговый коэффициент корреляции Спирмена в качестве меры связи двух признаков; ранговые критерии в качестве критериев проверки статистических гипотез, например, ранговый критерий Манна – Уитни при проверке гипотезы об однородности двух выборок или критерий Краскела – Уоллиса для проверки гипотезы об однородности более двух выборок. Измеренные в ранговой (порядковой) шкале порядковые переменные позволяют ранжировать (упорядочить) объекты, указав, какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной. Однако они не позволяют сказать «на сколько больше» или «на сколько меньше».
Для интервальных переменных, характеризующих количественно объекты с помощью общей для всех объектов единицы измерения (возраст респондента, его зарплата и т.п.), используется параметрические характеристики: среднее арифметическое в качестве средней оценки, дисперсия – для оценки разброса, коэффициент линейной корреляции Пирсона – для оценки величины статистической связи между переменными; а также параметрические критерии, основанные на сравнении параметрических характеристик: t-критерий Стьюдента, основанный на сравнении средних при проверке гипотезы об однородности двух выборок или F-критерий параметрического дисперсионного анализа, основанный на сравнении дисперсий, при проверке гипотезы об однородности более двух выборок; кластерный и факторный анализы системы корреляционно связанных признаков (переменных), кластеризация (кластерный анализ) респондентов по совокупности признаков на основании параметрического дисперсионного анализа и т.д.
Результаты исследования и их обсуждение
Общее распределение респондентов по уровню образования представлено на рис. 1.
Согласно рис. 1 имеют высшее или среднее специальное образования 69 % пенсионеров Томской области.
Числовые характеристики распределения образования по уровням (О1 – О5) представлены в табл. 2.
Таблица 2
Параметры распределения образования по уровням
|
Индикатор |
Объем выборки |
Среднее |
Медиана |
Мин |
Макс |
Станд. отклон. |
Асимметрия |
Эксцесс |
|
№ 68 |
400 |
3,090 |
3 |
1 |
5 |
0,935 |
0,430 |
–0,516 |
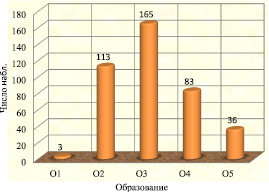
Рис. 1. Гистограмма частот образования
Рассмотрим проверку гипотез об однородности образования по номинальным индикаторам, а также связи образования с прочими ранговыми индикаторами благополучия старшего поколения Томской области на основе непараметрических (ранговых) критериев.
H1: Образование мужчин (М) и женщин (Ж) различается.
Согласно распределениям образования по уровням для мужчин (36 %) и женщин (64 %) основное различие касается уровней О2 (высшее образование) и О3 (среднее специальное образование). Среди мужчин чаще встречаются с высшим образованием (35 % с О2 и 29 % с О3), а среди женщин – со средним специальным (25 % с О2 и 48 % с О3). Однако эти различия оцениваются незначимыми (на уровне p > 0,10) согласно ранговому критерию Манна – Уитни (рис. 2).
H2: Образование в разных местах проживания (МП) различается.
Непараметрический (ранговый) критерий Краскела – Уоллиса выделяет 3 группы мест проживания, однородные по образованию, Томск, Асино {ТА – 56 % респондентов}, Северск {Сев – 14 %}, Каргасок, Teгульдет, Томский, Асиновский, Каргасокский районы {Рн – 30 %} и оценивает различие между образованием в разных местах проживания как статистически значимое (на уровне 0,050 > p ≈ 0,007 > 0,005) за счет сильно значимого (на уровне 0,0050 > p ≈ 0,0009 > 0,0005) отличия образования Сев от Рн и слабо значимого (на уровне 0,10 > p > 0,05) отличия образования ТА от Рн и Сев (рис. 2).
H3: Образование работающих (Работа, Да – 33 %) и неработающих (Работа, Нет – 67 %) пенсионеров различается.
На основании рангового критерия Манна – Уитни эти различия оцениваются как статистически значимые (на уровне 0,050 > p ≈ 0,010 > 0,005) (рис. 2).
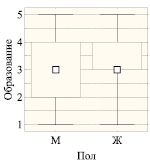
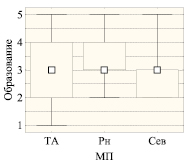
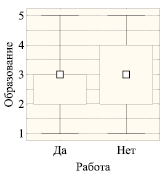
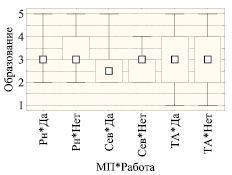
Рис. 2. Сравнение образования по номинальным индикаторам Пол, МП, Работа. Примечание. По ранговой шкале: квадраты – медианы, прямоугольники – 25–75 % квартильный размах, усы – полный размах
H4: Образование работающих и неработающих пенсионеров в разных местах проживания (МП*Раб) различается.
Непараметрический (ранговый) критерий Краскела – Уоллиса оценивает различие между образованием работающих и неработающих пенсионеров в разных местах проживания как сильно значимое (на уровне 0,0050 > p ≈ 0,0040 > 0,0005) за счет сильно значимого (на уровне 0,0050 > p ≈ 0,0013 > 0,0005) отличия образования работающих Томска и Асино (ТА*Да – 19 %) от неработающих в районах (Рн*Нет – 20 %), и статистически значимого (на уровне 0,050 > p ≈ 0,008 > 0,005) отличия образования работающих Северска (Сев*Да – 4 %) от Рн*Нет и статистически значимого (на уровне 0,050 > p ≈ 0,032 > 0,005) отличия образования работающих в районах (Рн*Да – 10 %) от Рн*Нет (рис. 2).
Таблица 3
Категории значимости парных коэффициентов корреляции
|
Категория значимости |
Незначимо |
Слабо значимо |
Статистически значимо |
Сильно значимо |
Высоко значимо |
|
Уровень значимости |
p > 0,10 |
0,10 > p > 0,05 |
0,05 > p > 0,005 |
0,005 > p > 0,0005 |
0,0005 > p |
|
Коэффициент корреляции |
r, R < 0,08 |
0,08 < r, R < 0,10 |
0,10 < r, R < 0,14 |
0,14 < r, R < 0, 17 |
r, R > 0, 17 |
Таблица 4
Матрица парных коэффициентов корреляций непараметрического (рангового) Спирмена R и параметрического Пирсона r между индикатором образования и прочими индикаторами благополучия старшего поколения
|
№ в анкете |
Смысловое содержание индикатора |
R |
r |
|
№ 1 |
С каким настроением Вы смотрите в будущее? |
0,28 |
0,27 |
|
№ 6 |
Удовлетворены ли Вы жилищными условиями? |
0,12 |
0,11 |
|
№ 7_2 |
Имеется ли у Вас в собственности компьютер (ноутбук)? |
0,21 |
0,21 |
|
№ 7_3 |
Имеется ли у Вас в собственности смартфон (планшет)? |
0,14 |
0,16 |
|
№ 13 |
Как Вы оцениваете Ваше здоровье? |
0,14 |
0,12 |
|
№ 32_2 |
Использование банковских услуг |
0,24 |
0,24 |
|
№ 32_5 |
Использование культурно-досуговых услуг |
0,19 |
0,19 |
|
№ 32_7 |
Использование платных бытовых услуг |
0,138 |
0,138 |
|
№ 34 |
Членство в каких-либо общественных организациях |
0,16 |
0,143 |
|
№ 36_3 |
Участие в защите окружающей среды |
0,16 |
0,16 |
|
№ 37_3 |
Общение с политиком или гос. чиновником |
0,13 |
0,12 |
|
№ 53_1 |
Желание пользоваться информационными технологиями |
0,13 |
0,12 |
|
№ 56_3 |
Общение с родными (друзьями) в социальных сетях |
0,23 |
0,21 |
|
№ 60_1 |
Финансовые возможности путешествовать |
0,29 |
0,31 |
|
№ 60_2 |
Финансовые возможности оплачивать мед. услуги |
0,23 |
0,24 |
|
№ 60_4 |
Финансовые возможности покупать качественные продукты |
0,20 |
0,20 |
|
№ 60_5 |
Финансовые возможности сменить бытовую технику |
0,15 |
0,15 |
|
№ 61 |
Умение использовать современные компьютерные устройства и технологии |
0,41 |
0,40 |
|
№ 62_1 |
Как часто Вы используете компьютер, ноутбук? |
0,42 |
0,41 |
|
№ 62_2 |
Как часто Вы используете планшет, смартфон? |
0,20 |
0,19 |
|
№ 62_3 |
Как часто Вы используете мобильный телефон? |
0,19 |
0,18 |
|
№ 62_4 |
Как часто Вы используете интернет? |
0,41 |
0,40 |
|
№ 63_1 |
Уровень Вашего навыка в общении в социальных сетях |
0,32 |
0,32 |
|
№ 63_2 |
Уровень навыка в поиске нужной информации в Интернете |
0,36 |
0,35 |
|
№ 63_3 |
Уровень навыка в интернет-покупках, оплачивании счета |
0,24 |
0,25 |
|
№ 63_4 |
Уровень навыка в скачивании фильмов, музыки |
0,25 |
0,26 |
|
№ 63_5 |
Уровень навыка в использовании электронной почты |
0,32 |
0,32 |
|
№ 63_6 |
Уровень навыка в общении по скайпу |
0,32 |
0,31 |
|
№ 63_7 |
Уровень навыка в игре в компьютерные игры |
0,21 |
0,22 |
|
№ 63_8 |
Уровень навыка в отправлении смс сообщения по мобильному телефону. |
0,31 |
0,29 |
|
№ 74 |
Доход Вашей семьи на одного члена в месяц |
0,30 |
0,30 |
|
№ 75 |
Материальное положение |
0,27 |
0,24 |
H5: Образование имеет значимые корреляционные связи с прочими ранговыми индикаторами благополучия старшего поколения Томской области.
Для переменных, измеренных в порядковой шкале, имеются свои типы корреляции, позволяющие оценить зависимости. Статистика R Спирмена для ранговых переменных может рассматриваться как прямой аналог статистики r Пирсона для переменных, измеренных в количественных шкалах. Рассмотрим основную гипотезу о корреляционной связи индикатора образования с прочими индикаторами благополучия старшего поколения. Корреляционный анализ этих показателей выявил разные уровни значимости (табл. 3) корреляционных связей разных пар показателей, один из которых – образование (табл. 4).
Следует заметить, что разница между R и r максимум в 0,03 оценивается в данном случае (400 респондентов) как незначимая (на уровне p > 0,10). Данное обстоятельство позволяет применить параметрический кластерный анализ индикаторов, имеющих значимую корреляционную связь с индикатором образования, на основе корреляционного расстояния (1 – r Пирсона) в качестве меры близости индикаторов. При этом в качестве правила объединения кластеров использован метод Варда на основе параметрического дисперсионного анализа. Графические результаты кластеризации таких индикаторов (табл. 4) представлены на дендрограмме (рис. 3). Устойчивыми относительно правила объединения кластеров (методы Варда, полной связи) можно считать формирование семи корреляционно связанных групп индикаторов, обозначенных F1 – F7.
Кластерный анализ позволяет выявлять значимые (1 – r ≤ 1 – 0,1 = 0,9 – критическое значение для группы из 400 респондентов при уровне значимости 0,05) кластеры индикаторов табл. 4, т.е. факторы для построения базиса пространства индикаторов табл. 4. С помощью факторного анализа методом главных компонент построена 7-факторная модель индикаторов табл. 5. Жирным шрифтом выделены наиболее значимые факторные нагрузки, которые позволяют по совокупности показателей интерпретировать значимые факторы. В нижней строке приведены весовые коэффициенты факторов.
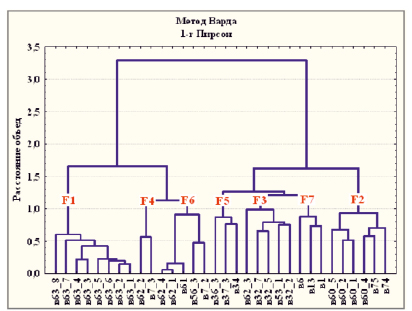
Рис. 3. Дендрограмма корреляционной матрицы индикаторов табл. 4
Таблица 5
Факторные нагрузки индикаторов табл. 4
|
Индикатор |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
|
№ 74 |
0,233 |
0,477 |
–0,030 |
0,455 |
0,053 |
–0,019 |
0,268 |
|
№ 75 |
0,096 |
0,658 |
–0,009 |
0,268 |
0,057 |
0,088 |
0,122 |
|
№ 1 |
–0,062 |
0,188 |
0,097 |
–0,026 |
0,158 |
0,169 |
0,629 |
|
№ 6 |
–0,143 |
0,148 |
–0,086 |
0,297 |
0,050 |
0,041 |
0,482 |
|
№ 7_2 |
0,286 |
–0,054 |
0,400 |
0,133 |
0,036 |
0,452 |
0,075 |
|
№ 7_3 |
0,073 |
–0,031 |
0,156 |
0,681 |
0,033 |
0,244 |
–0,004 |
|
№ 13 |
0,126 |
–0,011 |
0,167 |
–0,068 |
–0,047 |
–0,002 |
0,708 |
|
№ 32_2 |
0,140 |
0,231 |
0,590 |
–0,112 |
0,095 |
0,050 |
0,194 |
|
№ 32_5 |
0,073 |
0,085 |
0,649 |
0,030 |
0,062 |
0,077 |
0,152 |
|
№ 32_7 |
0,146 |
0,108 |
0,556 |
0,256 |
0,225 |
–0,024 |
–0,042 |
|
№ 34 |
0,079 |
–0,046 |
0,086 |
0,055 |
0,703 |
–0,024 |
0,179 |
|
№ 36_3 |
–0,027 |
–0,134 |
–0,021 |
–0,280 |
0,588 |
0,246 |
0,018 |
|
№ 37_3 |
0,122 |
0,216 |
0,113 |
0,164 |
0,579 |
–0,105 |
–0,183 |
|
№ 53_1 |
0,140 |
0,066 |
0,594 |
–0,016 |
–0,110 |
0,204 |
0,004 |
|
№ 56_3 |
0,336 |
–0,103 |
0,492 |
0,256 |
0,013 |
0,364 |
0,023 |
|
№ 60_1 |
0,299 |
0,517 |
0,004 |
–0,023 |
0,046 |
0,267 |
0,179 |
|
№ 60_2 |
0,264 |
0,613 |
0,117 |
–0,034 |
–0,045 |
0,092 |
–0,015 |
|
№ 60_4 |
0,088 |
0,649 |
0,119 |
0,020 |
0,139 |
0,046 |
–0,039 |
|
№ 60_5 |
0,136 |
0,629 |
0,138 |
–0,156 |
–0,267 |
0,131 |
0,049 |
|
№ 61 |
0,572 |
0,109 |
0,078 |
0,051 |
0,039 |
0,679 |
0,091 |
|
№ 62_1 |
0,530 |
0,081 |
0,088 |
0,120 |
–0,004 |
0,743 |
0,058 |
|
№ 62_2 |
0,232 |
0,110 |
0,005 |
0,571 |
–0,054 |
0,420 |
–0,158 |
|
№ 62_3 |
0,053 |
0,259 |
0,090 |
–0,261 |
0,178 |
0,403 |
–0,113 |
|
№ 62_4 |
0,553 |
0,098 |
0,077 |
0,149 |
–0,017 |
0,719 |
0,026 |
|
№ 63_1 |
0,866 |
0,075 |
0,122 |
0,070 |
–0,013 |
0,227 |
0,009 |
|
№ 63_2 |
0,837 |
0,130 |
0,093 |
0,005 |
0,020 |
0,371 |
0,005 |
|
№ 63_3 |
0,872 |
0,067 |
0,013 |
0,027 |
0,000 |
–0,002 |
–0,009 |
|
№ 63_4 |
0,860 |
0,063 |
0,060 |
0,039 |
0,031 |
0,042 |
0,042 |
|
№ 63_5 |
0,861 |
0,048 |
0,066 |
0,091 |
0,026 |
0,173 |
–0,005 |
|
№ 63_6 |
0,824 |
0,056 |
0,073 |
0,054 |
–0,007 |
0,297 |
–0,045 |
|
№ 63_7 |
0,760 |
0,052 |
–0,064 |
–0,016 |
0,166 |
–0,015 |
0,052 |
|
№ 63_8 |
0,644 |
0,128 |
0,154 |
–0,134 |
–0,010 |
0,154 |
0,081 |
|
Expl.Var |
6,965 |
2,569 |
2,064 |
1,605 |
1,529 |
3,008 |
1,537 |
|
Prp.Totl |
0,211 |
0,078 |
0,063 |
0,049 |
0,046 |
0,091 |
0,047 |
Примененный метод главных компонент является обобщением корреляционно-регрессионного анализа на случай системы многих индикаторов, среди которых не все являются линейно независимыми друг относительно друга. Если существуют зависимые между собой (коррелированные) величины, то их можно исключить переходом к новым «главным» и «некоррелированным» переменным величинам (факторам Fk). На простейшем примере системы двух случайных величин зависимость между переменными можно обнаружить с помощью диаграммы рассеяния. Полученная путем подгонки линия регрессии дает графическое представление зависимости. Если определить новую переменную на основе линии регрессии, изображенной на этой диаграмме, то такая переменная будет включать в себя наиболее существенные черты обеих переменных. Фактически, происходит сокращение числа переменных и замена двух одной. Отметим, что новая переменная (фактор) в действительности является линейной комбинацией двух исходных переменных. Пример, в котором две коррелированные переменные объединены в один фактор, показывает главную идею анализа главных компонент. Если пример с двумя переменными распространить на большее число переменных, то вычисления становятся сложнее, однако основной принцип представления двух или более зависимых переменных одним фактором остается в силе. В том случае, когда имеются три коррелированные переменные, можно построить 3-х мерную диаграмму рассеяния точно так же, как в случае двух переменных плоскую диаграмму рассеяния. Снова можно построить прямую регрессии, но уже в трехмерном пространстве. Для случая более трех переменных становится невозможным представить точки на диаграмме рассеяния, однако логика вращения осей с целью максимизации дисперсии нового фактора остается прежней. После того, как вы нашли линию, для которой дисперсия максимальна, вокруг нее остается некоторый разброс данных, на основании которого повторяется процедура выделения направления максимальной остаточной дисперсии. В анализе главных компонент именно так и делается: после того, как первый фактор выделен, то есть после того, как первая линия проведена, определяется следующая линия, максимизирующая остаточную вариацию (разброс данных вокруг первой прямой), и т.д. Таким образом, последовательно выделяются факторы, один за другим. Так как каждый последующий фактор определяется так, чтобы максимизировать изменчивость, оставшуюся от предыдущих, то факторы оказываются независимыми друг от друга, то есть некоррелированными или ортогональными. Результатом будет новый факторный набор переменных (главных компонент Fk), которые являются не коррелирующими и линейными комбинациями первоначальных индикаторов. В основном процедура выделения главных компонент подобна вращению, максимизирующему дисперсию (варимакс) исходного пространства индикаторов. Например, на диаграмме рассеяния можно рассматривать прямую регрессии как новую (факторную) ось. Этот тип вращения называется вращением, максимизирующим дисперсию, так как цель вращения заключается в максимизации дисперсии (изменчивости) новой переменной (фактора) и минимизации разброса вокруг нее. Новый набор факторных осей, проходящих через центр облака точек исходного пространства, получен в пространстве меньшей размерности. Геометрически цель состоит в том, чтобы получить набор ортогональных факторных векторов, где каждый вектор образует прямую линию в векторном пространстве исходных переменных. Эти векторы называются осями факторов и в дальнейшем используются для вычисления факторных координат точек наблюдений, что позволяет классифицировать наблюдения по категориям.
Факторный анализ является естественным обобщением и развитием метода главных компонент. Если объект описывается с помощью системы индикаторов, то в результате действия метода получается математическая модель, зависящая от меньшего числа переменных (факторов). При этом предполагается, что на исходные измеряемые данные оказывает влияние небольшое число латентных (скрытых) признаков (факторов). Цель факторного анализа заключается в выявлении этих скрытых характеристик (факторов) и оценивании их числа. Факторный анализ преследует две главные цели: сокращение числа индикаторов (редукция данных) и определение структуры взаимосвязей между индикаторами, т.е. классификация индикаторов. Поэтому факторный анализ используется или как метод сокращения данных или как метод классификации. Факторный анализ как метод редукции данных основан на использовании зависимости между индикаторами: вводится новая переменная (фактор) на основе регрессии, то есть включающая в себя наиболее существенные черты исходных индикаторов, так что ее использование (замена нескольких старых коррелированных индикаторов одной новой переменной (фактором)) приводит к сокращению числа переменных. При этом новый фактор представляется линейной комбинацией исходных индикаторов. Принцип представления двух или более зависимых переменных одним фактором демонстрирует главную идею факторного анализа или, более точно, анализа главных компонент. После выделения первого фактора, то есть построения первой линии регрессии, для которой дисперсия максимальна, определяется следующая линия, максимизирующая остаточную вариацию (разброс данных вокруг первой прямой), то есть выделяется второй фактор, и т.д. Факторы выделяются один за другим так, чтобы максимизировать изменчивость, оставшуюся от предыдущих, то есть оказываются независимыми друг от друга. Другими словами, некоррелированными или ортогональными. Отметим, что в процессе последовательного выделения факторов они включают в себя все меньше и меньше изменчивости. Решение о том, когда следует остановить процедуру выделения факторов, главным образом зависит от точки зрения на то, что считать малой «случайной» изменчивостью. Это решение достаточно произвольно, однако имеются некоторые общие рекомендации, позволяющие рационально выбрать число факторов: критерий накопленной или кумулятивной дисперсии, критерий Кайзера, критерий каменистой осыпи, содержательная интерпретация полученного решения. Поэтому обычно исследуется несколько решений с большим или меньшим числом факторов (факторных моделей), и затем выбирается одно наиболее «осмысленное». Факторный анализ как метод классификации основан на оценках корреляций (факторных нагрузок) между исходными индикаторами и факторами (или «новыми» переменными) в рамках выбранной факторной модели и позволяет узнать значимость факторов, то есть можно ли интерпретировать их разумным образом и как это сделать. Факторные нагрузки можно изобразить в виде диаграммы рассеяния, на которой каждая исходная переменная (индикатор) представлена точкой в координатах «факторные нагрузки». Можно повернуть оси в любом направлении без изменения относительного положения точек; однако действительные координаты точек, то есть факторные нагрузки, должны, без сомнения, меняться. Одним из типичных методов вращения является варимакс, описанный выше. Целью вращения является получение понятной (интерпретируемой) матрицы нагрузок, то есть факторов, которые ясно отмечены высокими нагрузками для некоторых переменных и низкими – для других, что и позволяет провести классификацию переменных.
Факторные индикаторы, построенные по индикаторам табл. 4, проинтерпретированы в табл. 6.
В результате проведения факторного анализа из 32 исходных индикаторов сформировано 7 значимых факторов.
Для оценки тесноты связи между стандартизированными значениями индикатора образования № 68ст и факторными индикаторами построим множественную регрессию:
№ 68cт = 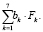
Оценки частных коэффициентов корреляции (bk) № 68ст и факторными индикаторами, а также значимости (pk) их отличия от ноля приведены в табл. 7.
Согласно табл. 7, № 68 ст связано высоко значимо (на уровне 0,00050 > p) только с 5 из 7 факторных индикаторов (F1, F2, F5, F6, F7) и незначимо (на уровне p > 0,10) – с 2-мя (F3, F4). Причем рассмотрение регрессии в стандартизированной шкале позволяет ранжировать факторы по силе их связи с образованием: F6 > F7 > F5 > F2 > F1.
Представляет интерес сравнительный анализ по показателю образования пенсионеров Томской области разных баз данных: выше рассмотренной Томск – 400 2015 г. (T15) и «Комплексное обследование условий жизни» по Томской области (К14) в рамках Федерального комплексного статистического наблюдение октября 2014 г. условий жизни населения Томской области, в котором участвовали 354 респондента старше 55 лет [2].
Таблица 6
Значимые взвешенные факторы, построенные по индикаторам табл. 4
|
№ |
Код фактора |
Вес |
Интерпретация факторов |
|
F1 |
№ 63_1-8 + № 61 + № 62_1,4 |
0,211 |
Уровень навыка в использовании современных компьютерных устройств и технологий |
|
F2 |
№ 75 + № 60_2,4,5 + № 60_1 + № 74 |
0,078 |
Наличие финансовых возможностей |
|
F3 |
№ 32_2,5,7 + № 53_1 + № 56_3 + № 7_2 |
0,063 |
Использование финансовых возможностей |
|
F4 |
№ 7_3 + № 62_2 + № 74 |
0,049 |
Использование собственного планшета, смартфона |
|
F5 |
№ 34 + № 36_3 + № 37_3 |
0,046 |
Социальная активность |
|
F6 |
№ 61 + № 62_1,4 + № 62_2,3 + № 7_2 |
0,091 |
Умение использовать компьютер, ноутбук, интернет, смартфон, мобильный телефон |
|
F7 |
№ 1 + № 13 + № 6 |
0,047 |
Чувство оптимизма (на основе удовлетворенности здоровьем и жилищными условиями) |
Таблица 7
Multiple Regression Results№ 68сt and Fk (k = 1, 2, …,7)
|
№ 68ст |
bk |
Std.Err.bk |
tk(392) |
pk-value |
|
F1 |
0,235 |
0,038 |
6,247 |
0,000 |
|
F2 |
0,265 |
0,038 |
7,047 |
0,000 |
|
F3 |
0,010 |
0,038 |
0,257 |
0,797 |
|
F4 |
0,038 |
0,038 |
1,018 |
0,309 |
|
F5 |
0,282 |
0,038 |
7,476 |
0,000 |
|
F6 |
0,388 |
0,038 |
10,302 |
0,000 |
|
F7 |
0,294 |
0,038 |
7,808 |
0,000 |
Таблица 8
Структура анкетных данных социологического опроса на примере показателя образования базы данных К14
|
№ вопроса |
Вопрос |
Вариант ответа (уровень образования ) |
Ранг ответа |
|
I07_01 |
Какое образование Вы имеете? |
Послевузовское |
1 |
|
Высшее бакалавриат |
2 |
||
|
Высшее специалитет, магистратура |
3 |
||
|
Неполное высшее (незаконченное высшее) – оконченные 3 курса и более |
4 |
||
|
Среднее профессиональное |
5 |
||
|
Начальное профессиональное |
6 |
||
|
Среднее общее |
7 |
||
|
Основное общее |
8 |
||
|
Не имеете основного общего |
9 |
Так как опросы проводят разные научные группы и с разными целями, то различия в формулировках и ранжировании ответов в подобных случаях – обычное дело. Тем не менее, несмотря на указанные различия, а также годовую разницу проведения опросов, сделана попытка сравнить данные выборки по показателю образования. При этом шкала ответов на вопрос I07.01 (К14) приведена в соответствии с № 68 (T15) посредством объединения ответов 2-го + 3-го, 4-го + 5-го + 6-го и 8-го + 9-го (табл. 8).
Заметим, что, согласно теории измерительных шкал, оценочная шкала уровней образования относится к типу порядковых шкал, позволяющих ранжировать (упорядочить) объекты, оценить качественнорезультаты на уровне отношений «<», « > « и «=», но не допускающих возможности введения эталонной единицы измерений образования для количественного измерения различий объектов, то есть оценочная шкала не является числовой измерительной шкалой. Поэтому в оценочной шкале использование операции среднего арифметического (и прочих конкретных математических формул) для сравнения является некорректным. В оценочной шкале обоснованным является использование медианы в качестве средней оценки. В связи с этим для сравнения рассматриваемых выборок предлагается использовать ранговые (непараметрические) критерии, основанные на рангах, а не на средних значениях.Однако полностью игнорировать средние арифметические нецелесообразно из-за их привычности и распространенности. Поэтому представляется рациональным использовать одновременно оба метода – и метод средних арифметических рангов (баллов), и метод медианных рангов. Такая рекомендация находится в согласии с общенаучной концепцией устойчивости, рекомендующей применять различные методы для обработки одних и тех же данных с целью выделить выводы, получаемые одновременно при разных методах. Поэтому в данной работе проводится сопоставление результатов исследования непараметрическими и параметрическими критериями.
В данном случае различия между № 68 и I07.01 оцениваются незначимыми как по ранговому критерию Манна – Уитни (на уровне p ≈ 0,46 > 0,10), так и по параметрическому t-критерию Стьюдента (на уровне p ≈ 0,29 > 0,10).
Выводы
Проведен многомерный статистический анализ влияния уровня образования на благополучие старшего поколения Томской области. На основе непараметрических (ранговых) критериев дисперсионного анализа оценено различие образования по полу как незначимое, по месту проживания и по работе – как статистически значимое.Корреляционный анализ выявил значимые связи уровня образования пожилых людей с 32 прочими ранговыми индикаторами благополучия старшего поколения Томской области. С помощью факторного анализа методом главных компонентов построена 7-факторная модель индикаторов, имеющих значимую корреляционную связь с индикатором образования. Регрессионный анализ оценил как высоко значимую связь между значениями индикатора уровня образования и пятью факторными индикаторами, ранжированными по силе их связи с образованием: F6 (Умение использовать компьютер) > F7 (Чувство оптимизма) > F5 (Социальная активность) > F2 (Финансовые возможности) > F1 (Уровень навыка в использовании компьютерными технологиями). Проведен сравнительный анализ по показателю образования пенсионеров Томской областии сходной базы данных с базой Федерального комплексного статистического наблюдения октября 2014 г. условий жизни населения Томской области (354 респондента старше 55 лет) и получена оценка их незначимого различия (на уровне p > 0,10) как по ранговому критерию Манна – Уитни, так и по параметрическом уt-критерию.
Эта работа была выполнена авторами в сотрудничестве с Томским политехническим университетом в рамках проекта по оценке и повышению социального, экономического и эмоционального благополучия пожилых людей в соответствии с Соглашением № 14.Z50.31.0029.
Библиографическая ссылка
Барышева Г.А., Михальчук А.А., Недоспасова О.П., Беркалов С.В., Задорожный В.Н., Терехина Л.И., Касати Ф. СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЛИЯНИЯ ОБРАЗОВАНИЯ НА БЛАГОПОЛУЧИЕ СТАРШЕГО ПОКОЛЕНИЯ ТОМСКОЙ ОБЛАСТИ // Фундаментальные исследования. 2017. № 8-2. С. 357-367;URL: https://fundamental-research.ru/ru/article/view?id=41674 (дата обращения: 05.01.2026).



