Рассматриваются технологические процессы с одним главным параметром качества и одном главным параметром управления.
Изложенные в статье результаты являются приложением фундаментальных теорем теории множеств и поэтому не имеют как отечественных, так и зарубежных аналогов. Доказательство основной теоремы о размерности, как уже опубликованное ранее, не приводится. Основным результатом, подлежащим прикладной интерпретации, является теорема о не более чем трёхмерности пространства с ориентированными друг относительно друга осями, и следующие из неё теоремы об ограниченности размерности суперпозиций.
Обычное евклидово пространство таково, что его оси не отличаются друг от друга, разве что обозначениями: например это первая ось, а это вторая, для плоскости, но ничто не мешает поменять обозначения, – изначально порядок осей не задан.
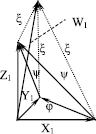
Рис. 1. Отображения φ, ψ, ξ ориентируют 4-мерие
Пространства с ориентированными осями таковы, что между направляющими векторами осей пространства задаются ориентирующие векторы, однозначно определяющие порядок осей. Причём для 3-мерных пространств ориентирующие векторы не образуют цикла. Для предполагаемого 4-мерного пространства с ориентированными осями доказано, что в нём возникает противоречивая ориентация, поэтому из этого следует, что пространства с ориентированными друг относительно друга осями не более чем трёхмерны [1, с. 26]:
Теорема 1 (об ограничении размерности). Пространства с ориентированными друг относительно друга осями не более чем трёхмерны.
Интерпретация ограниченности размерности в терминах суперпозиций
Как указано автором в [1], «cвойства оператора суперпозиции
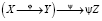(1)
неоднократно описывались, см., например, работы [2, 3].
Вопрос: возможно ли продолжение вложения суперпозиций вида
(2)
и т.д., – разрешим. На основании приложения теоремы 1 об ограничении размерности ориентированных пространств (их не более чем 3-мерности), показано, что допустимы cуперпозиции только вида (1), а суперпозиции вида (2) и большей вложенности – невозможны» [1, с. 85].
При рассмотрении оператора суперпозиции одномерных пространств вида
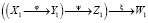, (3)
в котором отображения φ, ψ, ξ задают ориентации этих пространств (см. рис. 1) автором доказана теорема:
«Теорема 2 (об ограниченности суперпозиций для одномерных пространств). Для одномерных пространств Хi, имеющих общее начало координат в суперпозиции отображений
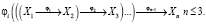
Иная формулировка теоремы:
Теорема 2’ (о том же). Для одномерных пространств, имеющих общее начало координат, суперпозиция
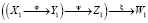
невозможна, возможна суперпозиция только для трех пространств, например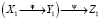
[1, c. 85–87].
Интерпретация теоремы о размерности в терминах задачи управления качеством
Как указывалось автором ранее в [4]: «в смысле теоремы 2, структура классической задачи управления – трёхмерна. Постановка классической задачи управления такова [5, с. 16]. Объект управления описывается системой дифференциальных уравнений
dxi/dt = fi(x1(t),…, xn(t), u1(t),…, um(t)) (4)
в векторной форме: dХ/dt = F(X(t), U(t)), где Х – это вектор координат, U – вектор управлений; fi непрерывно дифференцируемы; при этом имеется функция f0(X(t), U(t)), и задача управления сводится к минимизации функционала
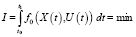(4')
путём выбора оптимального управления U(t), при перемещении точки из X0 = Х(t0) в X1 = Х(t1).
Записанные в терминах теоремы 2 отображения, соответствующие задаче (4), таковы: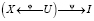 
, где отображение j задаётся системой дифференциальных уравнений (4), а y – минимизацией функционала (4'). Тем самым показано: структура классической задачи управления – трёхмерна в смысле теоремы 2 (если рассматриваются оптимальные процессы с параметрами (см. подробнее [5, с. 215–221]), где помимо управления U имеется параметр W, остающийся постоянным в процессе движения, то трёхмерность также налицо: 
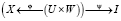[4]) [4, с. 16–17].
Обобщение задачи при возмущениях подробно рассмотрено в [4], при этом структура задачи также остаётся трёхмерной.
Структура задачи управления качеством процесса
Как указывалось автором ранее в [6]: «Решение задачи управления качеством технологического процесса при фундаментальной обоснованности трёхмерности пространства состояний системы:
1) параметр качества продукта (подпространство Х);
2) параметр управления (подпространство Y);
3) экономический параметр (подпространство Z) – соответствует суперпозиционному отображению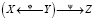 
.
Отображение φ – это отображение подпространства параметра управления Y в подпространство параметра качества X, отображение ψ – это отображение отображения φ в подпространство экономического параметра. Оптимум управления находится как управление при получении продукта, соответствующего норме качества с заданной вероятностью при минимальных издержках [7].
При этом в окрестности оптимума отображение φ допускает линеаризацию:
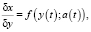(5)
где х – значение параметра качества, у – значение параметра управления (y* – оптимум), а – возмущение, f – функционал от параметров на промежутке управления. При линеаризирующем преобразовании получается
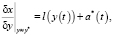(6)
где l – линейный функционал на промежутке управления. Статистическая фильтрация позволяет устранить влияние стохастических возмущений a*(t) на управление:
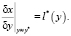(7)
При этом в задаче управления, в первом приближении, минимизируется функционал (задаваемый на ограниченном промежутке учёта параметров системы, – промежутке управления):
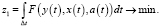
При учёте же экономической составляющей процесса производства, минимизация функционала (дополнительных издержек) выполнима относительно произведённого продукта, при уже отфильтрованных (7):
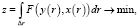(8)
при этом (8) раскладывается в сумму двух составляющих (в окрестности оптимума, с учётом (7)):
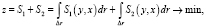
где S1 – дополнительные издержки, S2 – упущенная выгода. (Описание конкретных примеров задач см. в [7]).
Постановка задачи управления в вышеприведённых терминах в методе пространства состояний управления качеством такова. Система описывается уравнением
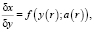(9)
допускающим вблизи оптимума линеаризирующую аппроксимацию (7), при этом минимизируется функционал дополнительных издержек (8).
Структура задачи трёхмерна
. (10)
То есть в методе пространства состояний, в отличие от классической задачи управления (см. [5, 8]) и её модификации при возмущениях [4], система уравнений или уравнение, описывающее объект (9), (7), отвлечено от понятия времени (в уравнение дифференцирование по параметру управления) и функционал (8) отвлечёт от времени (интегрирование в нём по произведённому продукту) – задача не «во» времени, а «над» временем» [6, с. 73–74].
Таким образом, прослежена аналогия (трёхмерность структуры задачи управления) и отличие задачи управления качеством технологических процессов от классической задачи управления, при сохранении общей трёхмерности структуры задачи управления качеством.
Методика управления качеством технологического процесса и её обобщение
В качестве простого примера приложения абстрактной пока задачи управления к конкретным технологическим процессам рассмотрена задача управления качеством процесса вакуумной сепарации губчатого титана. Методика управления длительностью процесса вакуумной сепарации губчатого титана описана в [7].
В процессе вакуумной сепарации при постоянной температуре под вакуумом происходит отгонка остатка магния и хлорида магния из блока титановой губки [9]. Ввиду того, что пористость титановой губки зависит от протекания предыдущей стадии процесса (восстановления четырёххлористого титана магнием, после чего следует слив из реторты магния и хлорида магния), при этом размер пор неконтролируем и неидентифицируем, – скорость испарения остатков магния и хлорида магния изменчива от реторты к реторте, и даже в отдельных частях блока титановой губки в одной реторте. Поэтому длительность отгонки остатков хлорида магния и магния изменчива от реторты к реторте. Главным параметром качества для этого процесса является остаточное содержание хлорида магния в толще титановой губки (определяемое уже после окончания процесса и вскрытия реторты), главным параметром управления (с учётом того, что температура и степень разряжения в реторте стабилизирован системой управления) является длительность процесса. Процессы, в которых блок титановой губки является содержащим значительную долю мелких пор, требуют большей длительности для отгонки хлорида магния (магний как более легкокипящий компонент отгоняется на начальной стадии процесса).
Методика управления процессом представляет собой приложение рассмотренной в параграфе 2 задачи управления к конкретному процессу и заключается в следующем [7]:
1. Определяются главный параметр качества X (содержание хлорида магния) и главный параметр управления Y (длительность процесса).
2. Строится приближённая математическая модель, определяющая момент теоретического окончания процесса (определяющая момент стабилизации энергопотока в реторту, по данным о мощности нагревателей).
3. Указанный момент теоретического окончания процесса принимается за единицу перенормированного одномерного пространства параметра управления процессом Y*.
4. Поскольку в п. 2 использовалась приближённая модель, то результаты её применения (момент теоретического окончания процесса) корректируются статистически при изображении результатов технологических процессов в пространстве двух параметров: перенормированного параметра управления Y* и параметра качества процесса Х, для определения коэффициента продления процессов относительно теоретического значения, см. рис. 2, 3.
5. При этом в п. 4 при определении коэффициента продления процессов используется принцип малой вариации параметра управления процесса [7, с. 69], позволяющий идентифицировать линеаризуемую зависимость параметра качества от перенормированного параметра управления.
6. При необходимости добавляется экономический параметр Z (особенности добавления экономического параметра приведены в [7]).
Управление качеством при этом заключается в адаптивном, по обработке данных о процессах, определении оптимального коэффициента продления длительности процессов (определении оптимального значения параметра Y*) относительно теоретического момента его окончания, по критерию достижения заданного качества (нормы содержания хлорида магния) с заданной вероятностью (p = 0,99), см. рис. 2, 3 (при большем коэффициенте относительного продления процессов качество выше, но выше и стоимость процесса).
Таковы общие составляющие методики управления указанным процессом, более подробно см. [7].
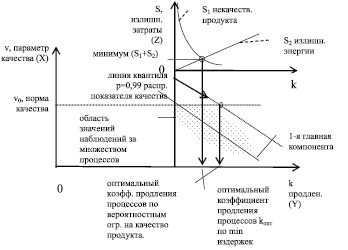
Рис. 2. Пример статистической диаграммы для процесса
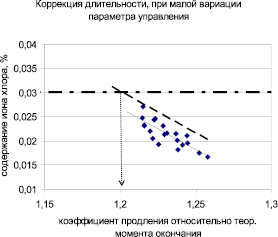
Рис. 3. Диаграмма выборки процессов при малой вариации параметра управления, «¦» – данные о процессах, «–––» – регрессионная прямая, «– - –» – линия нормы качества, «– –» – линия технологического доверительного интервала
Легко заметить, что особенными для указанного процесса являются п. 1 – определение параметра качества для данного процесса, и п. 2 – использование приближённой математической модели этого процесса. Остальные пункты (п. 3–6) не привязаны к специфике процесса. Поэтому легко убедиться, что управление другими технологическими процессами, содержащими один параметр качества, зависящий от одного параметра управления, следует той же методической схеме.
Аналогично построение управления и для процесса хлорирования титаносодержащей шихты (полное описание и диаграммы в [7]), методика управления содержанием в расплаве окиси титана такова (для управления содержанием углерода аналогично):
1. Определяются главный параметр качества Х (содержание в расплаве окиси титана) и главный параметр управления Y (стехиометрический коэффициент потока шихты на единицу стабилизированного потока хлора).
2. Строится приближённая математическая модель стехиометрического соответствия, определяющая теоретическое количество потока титаносодержащей шихты (содержащей оксид титана), необходимой для прореагирования с потоком хлора в хлоратор.
3. Указанное теоретическое значение теоретического потока шихты принимается за единицу перенормированного одномерного пространства параметра управления процессом Y*.
4. Поскольку в п. 2 использовалась приближённая модель, то результаты её применения (теоретический поток шихты) корректируются статистически при изображении результатов технологических процессов в пространстве двух параметров: перенормированного параметра управления Y* и параметра качества процесса Х (получаемого из результатов периодического анализа готового продукта), для определения поправочного коэффициента избытка/недостатка потока шихты относительно теоретического значения.
5. При этом в п. 4 при определении коэффициента избытка потока шихты используется принцип малой вариации параметра управления процесса, позволяющий идентифицировать линеаризуемую зависимость параметра качества от перенормированного параметра управления.
Управление качеством при этом заключается в адаптивном, по обработке данных о процессах, определении оптимального коэффициента избытка/недостатка титаносодержащей шихты (определении оптимального значения параметра Y*) относительно теоретического значения, для достижения нормы заданного содержания оксида титана в среднем, см. рис. 4.
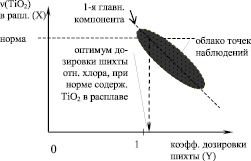
Рис. 4. Схема оптимизации баланса хлора и шихты
Для управления содержанием углерода в расплаве хлоратора: параметр качества Х – содержание углерода в расплаве, параметр управления Y – массопоток углерода в хлоратор, перенормировка параметра управления Y* по стехиометрическому коэффициенту необходимого углерода для связывания кислорода хлорируемых окислов.
Для непрерывного процесса сушки карналлита приложение обобщённой методики управления таково, как описано в [7]. Ещё пример – способ построения управления флегмовым числом ректификационной колонны, см. [10], ряд иных примеров для приложения методики см. в [7].
Таким образом, методика управления качеством технологического процесса обобщаема на ряд процессов с одним главным параметром качества и одним главным параметром управления. Наличие такого обобщённого подхода облегчает решение задач построения систем управления различными технологическими процессами в пределах ограничений на количество параметров качества и параметров управления.
Такой общий подход к управлению химико-технологическими процессами, наличием фундаментальных оснований трёхмерности структуры задачи управления, отличается от решения частных задач управления теми же процессами, описанными, например, в [11–13], см. также обзоры [14, 15].
Заключение
Показано, что методика управления качеством допускает обобщение на широкий ряд технологических процессов с одним параметром качества и одним параметром управления.
Это обобщение вытекает не из методики как таковой (если бы это было так, то вопрос «а почему методику невозможно построить иначе?» – оставался бы открытым). Обобщение вытекает из общей трёхмерной структуры задачи управления качеством технологического процесса, которая трёхмерна в силу свойства суперпозиций, описывающих пространство состояний технологического процесса (теорема 2), которое, в свою очередь, основано на теореме о размерности (теореме 1). В совокупности основания методики (теоремы 1, 2) указывают что методику (пространство состояний управляемого объекта) следует выбирать именно так, а не иначе; и то, что пространство состояний широкого класса технологических процессов описывается суперпозиционным отображением вида (10) даёт широкую область для приложения методики.
Отдельные конкретные приложения методики подробно изложены в [7], методика применена на ОАО «Соликамский магниевый завод» (однако детальные данные по технологическому процессу подпадают под определение «коммерческой тайны» и не могут быть опубликованы).
Библиографическая ссылка
Чечулин В.Л. УПРАВЛЕНИЕ ПАРАМЕТРАМИ ХИМИКО-ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ // Фундаментальные исследования. – 2017. – № 8-2. – С. 339-345;URL: https://fundamental-research.ru/ru/article/view?id=41671 (дата обращения: 03.12.2024).