Прогнозирование временных рядов финансовых активов является широким полем для исследования и применения эконометрических моделей. Данная область является весьма популярной в связи со своей практической значимостью, что в свою очередь побуждает исследователей применять различные типы моделей, порой достаточно сложные.
В данной работе была разработана и исследована торговая система на основе прогнозных значений, полученных с помощью комбинированной модели ARIMA/GARCH, для криптовалюты Bitcoin. На данный момент в обращении находится порядка 16 миллионов Bitcoin, а ежедневный объем торгов составляет порядка 275 тысяч транзакций, при цене более 2000 долларов за одну единицу криптовалюты [1]. Как и подобает финансовому активу, Bitcoin торгуется на специальных биржевых площадках, предназначенных для торговли криптовалютой. Исторические котировки для данной работы были взяты с биржи Bitstamp [2], являющейся второй по объему торгов.
Таким образом, в данной работе исследуется относительно новый финансовый актив, который развивается прямо сейчас. Целью работы является построение алгоритма принятия решений для биржевой торговой системы с последующим анализом полученных результатов. Решения о покупке или продаже криптовалюты осуществлялись на основе прогноза изменения цены для каждого следующего дня с помощью ARIMA/GARCH модели. Результаты каждого торгового дня фиксировались, и в конечном итоге был получен временной ряд доходности торговой системы, который был сопоставлен с временным рядом доходности самого актива. На основе сравнения статистических показателей двух временных рядов были сделаны выводы о целесообразности применения данной модели для торговли на бирже.
Модели типа ARIMA и GARCH применяются довольно часто для прогнозирования финансовых временных рядов. Для прогнозирования Bitcoin применялись модели нейронных сетей и другие методы машинного обучения [3], а также эконометрические методы (в том числе ARIMA и GARCH модели по отдельности [4]). Основное внимание в подобных исследованиях уделялось построению и оцениванию моделей, и результаты были представлены в виде статистических показателей моделей. В данной работе результатом является анализ торгового алгоритма. Подход, при котором анализируются показатели результатов торговой системы, а не только моделей, лежащих в ее основе, является, возможно, более удобным и понятным для инвестора, а также помогает оценить целесообразность применения модели.
ARIMA/GARCH модель
Модель типа ARIMA предназначается для исследования нестационарных временных рядов. Ряды можно привести к стационарному виду путем интегрирования исходного временного ряда. Модель обозначается ARIMA(p,d,q), где p, d и q – порядки соответственно авторегрессии, интегрированности и скользящего среднего.
Широкая известность модели ARIMA обусловлена ее эффективностью для прогнозирования временных рядов, порой превосходящей комплексные и более сложные модели. Использование модели ARIMA и других эконометрических моделей (VAR, СОУ) для прогнозирования временных рядов различных (макроэкономических) показателей рассматривалось в работах [5–7]. В модели ARIMA(p, d, q) прогнозируемое значение является линейной комбинацией прошлых значений (AR) и шума (MA) и имеет следующий вид:
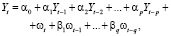
где ωt – белый шум, αi, βj – коэффициенты модели, Yt – значения ряда.
Модель типа GARCH [8] применяется для гетероскедастичных временных рядов, когда предполагается, что условная дисперсия ряда зависит от прошлых значений данного ряда. В этой модели используются прошлые значения дисперсии для прогнозирования будущих значений дисперсии временного ряда. Модель типа GARCH является обобщенным вариантом ARCH модели. Данные модели были предназначены для учета кластеризации волатильности на финансовых рынках. Феномен кластеризации волатильности был найден на широком спектре активов, поэтому логично было предположить, что данный эффект присутствует и на криптовалюте Bitcoin.
В то время как модель ARCH учитывает зависимость условной дисперсии только от квадратов прошлых значений временного ряда, модель GARCH предполагает, что условная дисперсия зависит также и от прошлых значений самой условной дисперсии. Модель обозначается GARCH(p, q), где p – порядок ARCH-членов, а q – порядок GARCH-членов. Для временного ряда ut модель выглядит следующим образом:
ut = ωtσt,
где ωt – белый шум, σt – стандартное отклонение, а условная дисперсия данного процесса будет равна
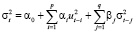 ,
,
где αi, βj – коэффициенты модели.
Таким образом, при помощи ARIMA и GARCH моделей можно прогнозировать следующее значение временного ряда, используя прошлые значения, шум и дисперсию. Затем обе модели были объединены в одну, а оптимальные параметры были подобраны на основе информационного критерия Акаике (AIC) [8]. При этом рассматривались модели ARIMA с p = 0, …, 5 и q = 0, …, 5 и GARCH c p = 1 и q = 1.
Описание торгового алгоритма
В качестве исторических данных использовались цены закрытия дня криптовалюты Bitcoin ($), взятые с биржи Bitstamp в период с 13 сентября 2011 года по 6 апреля 2017 года, что составило общую выборку объемом 2033 наблюдений [2]. Поскольку существует множество биржевых площадок, на которых торгуется криптовалюта, и цены на них различаются, стоит уточнить, что выбор источника данных обусловлен своей доступностью, качеством и достоверностью данных. В работе использовался язык программирования R и специализированные пакеты, предназначенные для статистической обработки данных (quantmod, lattice, timeSeries, rugarch и др.).
В основе торговой системы лежит комбинированный прогноз ARIMA/GARCH модели. С помощью скользящего окна длиной k дней составляется прогноз для каждого следующего дня. Параметры модели находятся методом перебора на выборке длиной k дней таким образом, чтобы минимизировать информационный критерий Акаике. Найденная таким способом лучшая модель используется для прогноза следующего дня, затем скользящее окно сдвигается на день вперед и процедура повторяется снова.
Исходный временной ряд цен актива (рис. 1) является нестационарным: расширенный тест Дики – Фуллера [8] показал (p-value = 0,5279), что нет оснований отвергать гипотезу о наличии единичного корня. Поэтому для получения стационарного ряда были взяты первые разности логарифмов цен актива (рис. 2). Полученный временной ряд является стационарным и подходит для использования модели. Расширенный тест Дики – Фуллера показал (p-value < 0,01), что гипотеза о наличии единичного корня отвергается.
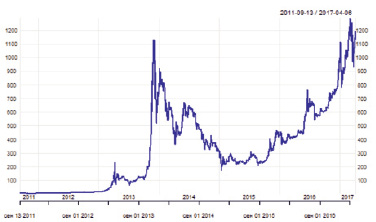
Рис. 1. Временной ряд цен закрытия дня Bitcoin (13.09.2011–06.04.2017)
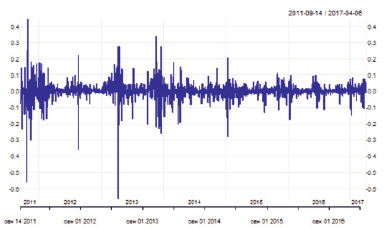
Рис. 2. Временной ряд разностей логарифмов цен Bitcoin (14.09.2011–06.04.2017)
Таким образом, результатом прогноза является величина приращения цены следующего дня. Что касается применения данного прогноза в торговой системе, следует отметить, что важно не значение данной величины, а только ее знак, который может быть положительным, отрицательным, либо значение равно нулю. Если величина имеет положительный знак, то покупается актив в начале торгового дня, если отрицательный, то открывается короткая позиция по активу, если значение прогноза равно нулю, то текущая позиция остается без изменений.
Торговля ведется всегда одинаковым количеством лотов, если подряд идет несколько прогнозов с одинаковым знаком, то в течение этого времени не увеличивается позиция, а остается однажды открытая позиция в данную сторону до тех пор, пока знак прогноза не изменится на противоположный. Также нет дней, когда не занимается направленная позиция, то есть позиция открыта всегда. Все описанные выше действия имитируются, и на основе этого получается временной ряд доходностей торговой системы, который анализируется и сравнивается с временным рядом цен самого актива. На основе подобного анализа можно судить о целесообразности применения данной торговой системы. Результаты имитации будут отличаться от результатов реальной торговли в худшую сторону, так как на рынке присутствуют дополнительные издержки. Например, получить цену на открытии дня, равную фактической цене открытия, практически невозможно, можно получить лишь приближенное к ней значение; также ликвидность имеет относительное значение для инвестора: большой объем денежных средств вызывает «проскальзывание» и ухудшает цену сделки, кроме того, существуют транзакционные издержки – комиссии биржи и брокера. Эти и другие издержки в данной работе не учитывались.
Для исследования были взяты максимально доступные (на момент исследования) данные (всего 2033 наблюдения). Поскольку данных не так много, а для оптимизации длины скользящего окна пришлось бы разделить выборку на две части, в данной работе было использовано (исходя из эмпирического опыта) скользящее окно k = 500 дням. Тем не менее величина скользящего окна – важный параметр, позволяющий подстраиваться под быстрые изменения, если свойства временного ряда имеют склонность меняться, либо извлекать максимум информации для прогноза, если свойства временного ряда более постоянны.
Для оценки качества построенной модели были протестированы остатки модели на наличие автокорреляции (рис. 3). В идеале, остатки должны представлять собой случайный процесс, не подверженный автокорреляциям. Тест Льюнг – Бокса [8] показал (p-value = 0,2476), что нет оснований отвергать нулевую гипотезу о том, что данные являются случайными, то есть автокорреляция отсутствует. Это позволило сделать вывод, что модель хорошо описывает рассматриваемые данные.
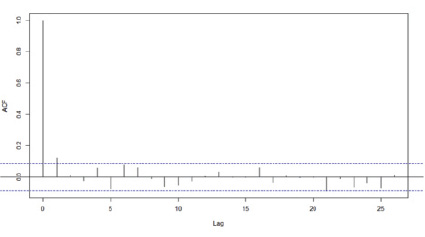
Рис. 3. Автокоррелограмма остатков модели
Результаты
Результаты торговой стратегии в сравнении с доходностью актива представлены в табл. 1. Для сравнения были выбраны следующие показатели: среднегодовая доходность, среднегодовое стандартное отклонение, коэффициент Шарпа (при нулевой процентной ставке) [9], максимальная просадка и коэффициент Кальмара [10].
Таблица 1
Показатели эффективности торговой стратегии и вложения средств в актив
|
Показатели |
Стратегия |
Bitcoin |
|
Доходность |
283 % |
277 % |
|
Стандартное отклонение |
143 % |
144 % |
|
Коэффициент Шарпа |
1,98 |
1,92 |
|
Максимальная просадка |
40 % |
47 % |
|
Коэффициент Кальмара |
5,96 |
4,89 |
Из табл. 1 видно незначительное преимущество торгового алгоритма по всем показателям. Наибольшие изменения произошли в показателях максимальной просадки и коэффициента Кальмара: максимальная просадка снизилась на 16 %, а коэффициент Кальмара вырос на 18 %. Коэффициент Шарпа улучшился всего на 3 %. Поскольку коэффициент Кальмара является соотношением средней геометрической доходности и максимальной просадки, то снижение показателя максимальной просадки ведет к закономерному увеличению данного коэффициента. А незначительное увеличение коэффициента Шарпа обусловлено малыми изменениями в показателях средней арифметической доходности и стандартного отклонения, поскольку в данном случае коэффициент Шарпа является соотношением этих двух величин (при нулевой процентной ставке). Оба коэффициента являются показателями эффективности инвестиционного портфеля и представляют собой параметр, который оценивает риск и вознаграждения за этот риск.
Рассмотрим также показатели торговой стратегии на основе модели CAPM (модели оценки долгосрочных активов) [11] и методологии современной портфельной теории [10]: коэффициенты Альфа и Бета, коэффициент детерминации, коэффициент информации и коэффициент Трейнора [12]. Бенчмарком служит криптовалюта Bitcoin, безрисковая процентная ставка равна нулю. Результаты оценки параметров модели и показатели торговой стратегии на основе этой модели представлены в табл. 2.
Таблица 2
Результаты оценки параметров модели CAPM и показатели торговой стратегии на основе данной модели
|
Показатели |
Значения |
|
Альфа |
0,0021 (*) |
|
Бета |
0,1888 (***) |
|
Коэффициент детерминации |
0,364 |
|
Коэффициент информации |
0,06 |
|
Коэффициент Трейнора |
14,98 |
Примечание. Уровни значимости: * – 10 %;
** – 5 %; *** – 1 %
Оценки параметров модели CAPM были получены в результате построения модели линейной регрессии. Модель имеет следующий вид:
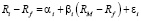 ,
,
где Ri – ожидаемая ставка доходности актива (стратегии), Rf – безрисковая процентная ставка, Ri – Rf – ожидаемая ставка доходности актива (стратегии) с учетом безрисковой процентной ставки, αi – коэффициент ожидаемой доходности актива (стратегии) по отношению к ожидаемой рыночной доходности, βi – коэффициент чувствительности актива (стратегии) к изменениям рыночной доходности, RM – ожидаемая рыночная доходность, RM – Rf – премия за риск, равная разнице ставок рыночной и безрисковой доходности, εi – некоррелированные ошибки модели.
Модель CAPM описывает отношения между рыночным риском и ожидаемой доходностью актива или торговой стратегии в данном случае. Модель широко используется в финансах и позволяет инвестору оценить перспективность вложения средств в инструмент, отличный от бенчмарка (например, отдельная акция, торговая стратегия или хедж-фонд), и учесть рыночный риск этого инструмента, доходность инструмента по отношению к бенчмарку и временную стоимость денег (в данном случае не учитывается, Ri = 0). В качестве бенчмарка были взяты цены закрытия дня Bitcoin, а в качестве инструмента для альтернативного вложения средств – результаты разработанной торговой стратегии за тот же период.
Коэффициент Альфа (α) позволяет определить инвестиционную привлекательность актива, а также оценить мастерство управляющего активами. Фактически данный коэффициент демонстрирует способность торговой стратегии (в данном случае) генерировать дополнительную доходность, никак не связанную с поведением бенчмарка. Для данной стратегии коэффициент Альфа оказался равен 0,0021 (значим на 10 % уровне значимости), что является довольно низким показателем. Коэффициент Бета (β) является своеобразной мерой рыночного риска. В отличие от стандартного отклонения, которое измеряет риск абсолютный, коэффициент Бета измеряет риск относительно взятого бенчмарка: чем больше Бета, тем с большей волатильностью движется цена актива относительно бенчмарка, и наоборот, коэффициент Бета, равный 1, означает, что актив движется вместе с бенчмарком. В данном случае коэффициент Бета равен 0,1888 (значим на 1 % уровне значимости). Это считается довольно низким значением и в свою очередь является привлекательным результатом, так как стратегия повторяет лишь 19 % волатильности бенчмарка, который сам по себе является крайне волатильным, а волатильность является мерой риска. Однако не все так однозначно, полученные среднегодовые стандартные отклонения бенчмарка и стратегии лишь незначительно отличаются друг от друга (незначимость различий дисперсий и средних двух выборок (в силу отсутствия нормальности распределения двух совокупностей) проверена с помощью непараметрических критериев Вилкоксона и Муда [13]). Скорее всего, данный эффект был вызван специфичностью движения доходности стратегии, и, если сравнивать результаты на более крупном таймфрейме (месячном или недельном), можно получить более высокий коэффициент Бета и, вероятно более релевантный.
Коэффициент детерминации тоже оказался достаточно низким: его значение равно 0,364. Это означает, что в среднем приблизительно 36 % вариации доходности торговой стратегии можно объяснить за счет вариации цен бенчмарка, также можно сказать, что большую часть времени поведение торговой стратегии отлично от бенчмарка. Коэффициент информации равен 0,06, что можно интерпретировать как крайне низкий показатель. Коэффициент информации наряду с коэффициентом Альфа является еще одним способом оценить мастерство управляющего. Он рассчитывается как отношение коэффициента Альфа к стандартному отклонению разности доходностей актива (торговой стратегии) и бенчмарка, так называемой ошибке слежения. Таким образом, данный коэффициент показывает, сколько единиц независимой доходности приходится на дополнительную единицу риска. Соответственно, чем выше значение коэффициента, тем это лучше для управляющего; хорошим считается значение, начинающееся с 0,5, следовательно, коэффициент информации данной торговой стратегии является неудовлетворительным.
Коэффициент Трейнора равен 14,98, что является крайне хорошим показателем. Он рассчитывается как отношение доходности стратегии к коэффициенту Бета, напоминая собой коэффициент Шарпа, с той лишь разницей, что в качестве меры риска берется так называемый систематический риск. Коэффициент показывает, сколько доходности приходится на единицу рыночного риска. Высокое значение коэффициента обусловлено низким значением коэффициента Бета. Ориентироваться на коэффициент Бета рекомендуется при коэффициенте детерминации выше 0,8. Применение альтернативных метрик дает возможность получения более объективного результата.
Заключение
В работе был описан процесс создания торговой стратегии на основе комбинированной модели ARIMA/GARCH, примененной на криптовалюте Bitcoin. Модель хорошо подходит для рассмотренных данных (автокорреляция в остатках отсутствует). Однако, торговая стратегия, в основе которой лежали прогнозы, полученные с помощью данной модели, не дала высоких результатов. Торговая стратегия незначительно опережала бенчмарк в своих показателях, однако статистические тесты доходностей стратегии и бенчмарка не показали значимых различий средних и дисперсий двух выборок. Также стратегия была оценена с помощью CAPM модели, получены Альфа и Бета коэффициенты и рассчитаны некоторые метрики на их основе. Стратегия генерирует сравнительно небольшой коэффициент Альфа порядка 0,2 %. Коэффициент Бета оказался на удивление низким, что является хорошим результатом, учитывая то, что дисперсии двух временных рядов значимо не различаются. Возможно данный эффект связан со специ-
фическим поведением кривой доходности стратегии, а также лучшими результатами в показателе максимальной просадки по сравнению с бенчмарком.
Тем не менее положительных результатов, полученных во всех перечисленных показателях, недостаточно, чтобы считать стратегию более привлекательной для инвестиций, чем бенчмарк. К тому же в данной работе не были учтены никакие виды издержек. Возможно, предложенная модель работает лучше на других таймфреймах (например, на недельных интервалах, или интервалах ниже дневных). Применение новых моделей и использование предложенных на новых данных оставляет за собой поле для будущих исследований.
Библиографическая ссылка
Суханова Е.И., Ширнаева С.Ю., Кожемякин Д.А. АНАЛИЗ ПРИБЫЛЬНОСТИ ТОРГОВОЙ СТРАТЕГИИ НА ОСНОВЕ ARIMA/GARCH МОДЕЛИ ДЛЯ РЫНКА BITCOIN // Фундаментальные исследования. 2017. № 8-1. С. 226-232;URL: https://fundamental-research.ru/ru/article/view?id=41652 (дата обращения: 07.03.2026).



