В условиях современной экономики, характеризующейся динамичностью, важное значение приобретает оптимизация управления организационно-экономическими системами, позволяющая сочетать высокую оборачиваемость финансово-материальных ресурсов в системе и за её пределами с риском возникновения дефицита, выполнять прогнозирование, повышать финансовую устойчивость, определять источники развития системы на основе внешних и внутренних факторов и проводить её комплексную реструктуризацию. Под организационно-экономической системой будем понимать «сложную взаимосвязанную совокупность элементов – организационно, экономически, а иногда и технологически связанных между собой подсистем более низкого уровня» [8].
Управлять производственно-накопительными процессами необходимо иерархической системой алгоритмов, в которой алгоритмы более высоких уровней осуществляют агрегированное согласование работы процессов нижележащего уровня. Задача согласования упрощается, если в организационно-экономической структуре системы между производственными процессами (ПП) осуществляются накопительные процессы (НП), образующие запасы материальных, трудовых или финансовых ресурсов. Использование накопительных процессов, благодаря сглаживанию влияния случайных факторов, позволяет повысить эффективность согласования производственных процессов.
При вероятностном моделировании производственно-накопительных процессов для целей управления возникают проблемы выбора класса моделей и методов моделирования. Чаще всего для этих целей используются методы теории управления запасами, методы статистических испытаний и экономического анализа [3, 4]. Задача управления запасами возникает тогда, когда необходимо создать финансовый или материальный запас с целью удовлетворения спроса на некотором интервале времени. Поэтому при решении задачи управления организационно-экономическими системами возникает необходимость в управлении финансовыми и материальными запасами, образующимися в накопительных процессах, связывающих систему с внешней средой по входу и выходу, так и в накопительных процессах, осуществляющих связь производственных процессах. Следовательно, для организационно-экономических систем возникает необходимость в решении двух видов задач управления запасами.
В задачах управления финансовыми или материальными запасами, образующимися в накопительных процессах, связывающих систему с внешней средой по входу и выходу, решаются вопросы выбора размеров и сроков размещения заказов на запасаемую (отгружаемую продукцию) или объемов всех видов финансовых поступлений в систему (оттоков из системы). Это стандартная задача теории управления запасами.
Наличие накопительных процессов, связывающих производственные элементы, определяет специфику управления финансовыми или материальными запасами. С одной стороны, финансово-материальные запасы позволяют уменьшить жесткость связей процессов, составляющих структуру организационно-экономической системы, и, следовательно, снизить требования к управлению. С другой стороны, наличие накопительных процессов увеличивает число вариантов задачи выбора управлений и требования к оптимальности и интегрированности системы.
Эти особенности производственно-накопительных процессов, как объекта управления, выдвигают специфические требования к системе управления. Во-первых, при управлении такими процессами среди прочих затрат учитываются стоимости товарно-материальных запасов и расходы на их хранение. Во-вторых, уровни запасов должны находиться в пределах допуска, выход из которых ведет к излишним потерям от связывания оборотных средств, дефициту или аварийным остановкам производственно-накопительных процессов, зачастую связанных с потерями от простоя, затратами на выведение технологии в рабочий режим, штрафами за несвоевременную поставку продукции потребителям, убытками от расторжения договоров. В-третьих, для учета временных и пространственных факторов система управления производственно-накопительными процессами должна быть иерархической.
Анализ методов и практики разработок систем управления запасами показывает, что вторая задача методами теории управления запасами не решается. Частная задача рассмотрена в некоторых работах. Однако при большом числе производственных и накопительных процессов и произвольной структуре их связей задача является сложной.
Следовательно, вероятностное моделирование производственно-накопительными процессами в рамках теории управления запасами полностью осуществить не удаётся, хотя понятия, термины и методы этой теории могут использоваться при построении рассматриваемых систем управления. Кроме того, для вероятностного анализа широко применяются методы статистических испытаний. Их применение для управления выделенным классом систем будет оправдано, если для части оценок получены конечные формулы, проведено упрощение структуры системы, например, по принципу узких мест, использованы альтернативные модели, выбираемые алгоритмом по требуемой точности вычислений.
Одной из сложных задач экономико-математического моделирования является получение оценок вероятностей выхода уровней запасов в накопительных процессах за пределы допуска. С этой целью могут быть использованы результаты исследований, изложенные в работах [2, 6, 7]. К сожалению, решения, описываемые на основе моделей этого класса, следует рассматривать скорее как принципиальные выводы, а не конкретные рекомендации для управления системами с накопительными процессами.
При решении задач стратегического планирования и оперативного управления необходимо использовать многоэтапную вероятностную модель траектории развития процесса и многоэтапную вероятностную модель планирования, ориентированную на получение с заданной, заранее установленной степенью вероятности выполнения планового задания и минимизирующую вероятность выхода уровней накопления за пределы допуска.
Как следует из обзора вероятностных моделей, к настоящему времени для организационно-экономических систем с производственно-накопительными процессами требуется проведение системных исследований задачи управления, которые могут быть выполнены с использованием методов декомпозиции.
Рассмотрим функционирование организационно-экономической системы на промежутке времени [O, T], разбитом на интервалы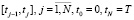 
,
осуществляемое в частично неконтролируемой среде, причем основное влияние стохастических факторов проявляется в непрогнозируемом сбое ПП, обусловленном различными причинами.
Будем предполагать, что в данной системе происходит N производственных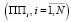 
и М одноресурсных накопительных процессов 
.
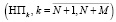Одна часть НП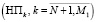 
осуществляет связь системы с внешней средой по входу, вторая часть 
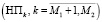осуществляет связь между ПП, а третья часть 
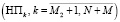связывает систему с внешней средой по выходу.
Структура производственно-накопительного процесса задается множеством Qk номеров ПП, осуществляющих связь с НПk по входу, множеством Рk номеров ПП, связанных с НПk по выходу, множеством Qi номеров НП, связанных с ППi по входу и множеством Рi номеров НП, осуществляющих связь с ППi по выходу.
Объемные статические модели ППi записываются в виде
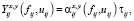
где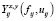 
– количество ресурса или продукта xi (или yi) потребляемого (или выпускаемого) ППi в интервале времени 
;
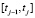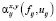– средняя интенсивность потребления ресурса xi (или выпуска продукта yi) в интервале 
;
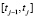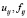– значения управляющего и возмущающего воздействия на ППi в интервале 
;
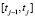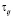– время работы ППi в интервале времени 
.
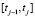Величины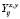 
и 
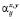представляют собой векторы, координатами которых являются, соответственно 
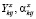и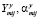 
,
где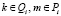 
. Уравнение связи между ПП и НП записывается в виде 
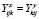и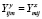 
. Использование различных типов производственных функций обсуждалось в работе [1].
Текущий уровень запаса в НПk в момент времени tj определяется из формулы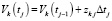 
, где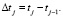 
Для НП, осуществляющих связь ПП, получаем
.
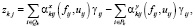
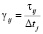Для НП, осуществляющих связь производства с внешней средой по входу,
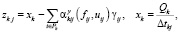
где xk – интенсивность поставок на НПk;
Qk – объем единовременной поставки на НПk;
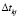– интервал времени между поставками НПk.
Для НП, осуществляющих связь производства с внешней средой по выходу,
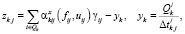
где yk – интенсивность отгрузки из НПk;
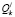– объем единовременной отгрузки из НПk;
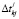– интервал времени между отгрузками из НПk.
В данной модели на интервале времени [О, Т] рассматривается трехуровневая система управления производственно-накопительными процессами, в которой верхний уровень, уровень планирования, осуществляет разбиение плана по пространственной структуре производства. Второй уровень (регулирования) выявляет отклонения фактических результатов от плановых в каждый из моментов времени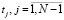 
и осуществляет проверку возможности выполнения плана на оставшемся интервале времени [tj, T]. Нижний уровень осуществляет непосредственное управление производственно-накопительными процессами.
На уровнях планирования и регулирования осуществляется пространственное согласование работы ПП с учетом планируемого или реального состояния производственных и накопительных процессов на рассматриваемом j-м интервале времени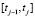 
и условия невыхода уровня накопления за пределы допуска.
В задаче планирования план экономическим или техническим звеньям получают на основе календарного плана всей системы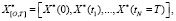 
где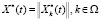 
– множество номеров накопительных процессов, для которых решена задача календарного планирования; а 
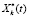– объем k-го ресурса (продукта), т.е. помещенного в НПk, за интервал [0, t].
Модель прогнозируемого в момент времени tj выпуска объема k-го ресурса (продукта) за [0, t] имеет вид
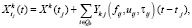
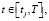
где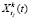 
– прогноз выпуска k-го ресурса (продукта) в момент времени tj;
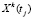– выпуск k-го ресурса (продукта) за [0, t].
Решение задачи планирования позволяет определить программу управления каждым ППi, связанным по выходу с НПk в следующем виде
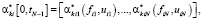
где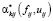 
– интенсивности работы ППi на интервале 
.
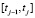Оперативное планирование целесообразно осуществлять в соответствии со следующим алгоритмом.
Шаг 1. Полагаем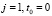 
.
Шаг 2. С учетом планируемых состояний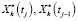 
определяем значения интенсивностей работ 
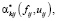лежащих в границах допустимой экономической или производственной мощности так, чтобы выполнялось равенство
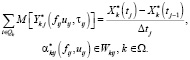
Шаг 3. Определяем интенсивности работ остальных ПП из условия невыхода уровня накопления за верхний и нижний пределы с максимальной вероятностью. При этом решаются задачи
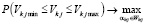
или
.
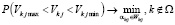Движение по экономической или производственной структуре производится, начиная от НП, осуществляющих связь производства с внешней средой по выходу, в направлении противоположном движению финансовых или материальных потоков.
Шаг 4. Полагаем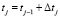 
, если 
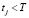, то переходим на шаг 2, иначе заканчиваем оперативное планирование.
Регулирование производственно-накопительных процессов предлагается осуществить в соответствии со следующим алгоритмом.
Шаг 1. Полагаем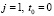 
и устанавливаем интенсивности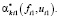 
Шаг 2. Полагаем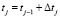 
, и если 
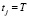, то конец очередного цикла управления.
Шаг 3. Измеряем объемы k-го ресурса (продукта)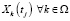 
и определяем прогнозируемые значения цели управления
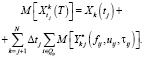
Шаг 4. Для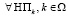 
проверяется условие 
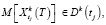где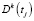 
– область значений, удовлетворяющая условиям
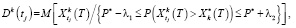
где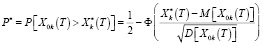 
– вероятность выполнения планового задания при реализации программной траектории 
;
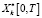λ1, λ2 – предельно допустимые уровни снижения и превышения вероятности выполнения планового задания;
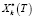– плановое задание для момента времени Т.
Шаг 5. Если условие шага 4 выполняется, то коррекция не проводится, т.е. реализуются интенсивности и переходим к шагу 9 алгоритма.
Шаг 6. Если условие шага 4 не выполняется, то анализируются возникшие отклонения. Если компенсировать отклонение на интервале [tj, T] не удается при имеющихся ресурсах, то осуществляется выход в подсистему более высокого уровня с целью корректировки планового задания на интервале [tj, T]. Если возникшие отклонения удается компенсировать, то вычисляются интенсивности, удовлетворяющие выражениям
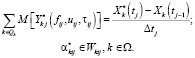
Шаг 7. Выполняется шаг 3 алгоритма оперативного планирования.
Шаг 8. Устанавливаем значения интенсивностей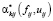 
и осуществляем переход к шагу 2 алгоритма.
Шаг 9. Проверяются условия выхода уровня накопления за установленные пределы с заданной вероятностью
.
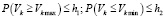Если данные условия выполняются, то выполняем переход к шагу 2 алгоритма. В противном случае возврат к шагу 7.
Таким образом, разработанные для модели алгоритмы планирования и регулирования могут быть конкретизированы до постановок задач, входящих в них для численного решения, и реализованы в виде моделирующего программного комплекса. В алгоритмах управления запасами наиболее трудоёмким является определение плотности распределения выполнения стратегического плана и плотности распределения текущего уровня запаса в НП, требующие вычисления композиции законов распределения времени безотказной работы ПП. В работе [5] рассмотрены способы вычисления композиций законов распределения при распределении времени безотказной работы ПП по усеченному нормальному закону и в классе кривых Пирсона.
Библиографическая ссылка
Мамченко О.П., Исаева О.В., Байкин А.А. ДИНАМИЧЕСКАЯ МОДЕЛЬ УПРАВЛЕНИЯ ПРОИЗВОДСТВЕННО-НАКОПИТЕЛЬНЫМИ ПРОЦЕССАМИ В ОРГАНИЗАЦИОННО-ЭКОНОМИЧЕСКИХ СИСТЕМАХ // Фундаментальные исследования. – 2017. – № 8-1. – С. 191-195;URL: https://fundamental-research.ru/ru/article/view?id=41645 (дата обращения: 09.10.2024).