Модель Лотки – Вольтерры отражает схему взаимодействия двух видов типа «хищник – жертва», она получила название в честь авторов, предложивших независимо друг от друга модельные уравнения [2, 3].
Эти уравнения применимы при моделировании различных типов взаимодействия между видами, таких как системы «хищник – жертва», «паразит – хозяин», конкуренции и так далее.
В математической форме предложенная система имеет следующий вид:
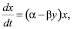
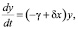
где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, отражающие взаимодействия между видами.
Для данной системы уравнений экспериментальным путем были подобраны значения коэффициентов для того, чтобы экосистема была в равновесии. Значения коэффициентов представлены в табл. 1.
Таблица 1
Подборка коэффициентов уравнений
|
Внешние коэффициенты |
Значение |
|
Коэффициент рождаемости жертв |
0,05 |
|
Коэффициент поедания (поглощения) |
0,0002 |
|
Коэффициент рождаемости хищников |
1 |
|
Коэффициент смертности хищников |
0,05 |
|
Начальная популяция жертв |
100 |
|
Начальная популяция хищников |
50 |
Модель была реализована в виде программного продукта для имитации модели, результат равновесной экосистемы представлен на рис. 1.
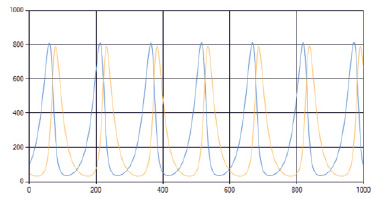
Рис. 1. Результат реализации модели хищник – жертва. По оси абсцисс – время моделирования,
по оси ординат – численность популяции
Можно заметить, что динамика развития популяции хищников и жертв имеет колебательный характер в силу присутствия сильных циклов с обратной связью, показанных на рис. 1. Эти силы заставляют популяции колебаться вокруг набора заданных условий.
Базируясь на модели Лотки – Вольтерры, формализуем процессы слияний и поглощений компаний по аналогии взаимоотношений в экосистеме «хищник – жертва», где хищники – крупный бизнес (транснациональные корпорации, холдинги, институциональные инвесторы), жертвы – малый и средний бизнес (стартапы, МИПы и т.д.) и государство как отдельный актор взаимодействия, осуществляющий свою часть финансирования деятельности стартапов.
Можно заметить, что динамика развития популяции хищников и жертв имеет колебательный характер в силу присутствия сильных циклов с обратной связью, показанных на рис. 1. Эти силы заставляют популяции колебаться вокруг набора заданных условий.
Следующим примером популяционных моделей является модель взаимодействия двух видов, конкурирующих между собой за один общий вид ресурса. В такой системе виды могут и не быть хищниками по отношению к другому виду. Например, несколько видов рыбы могут конкурировать за один источник пропитания, однако не пожирать друг друга. С другой стороны, существуют системы, где два вида конкурируют за один общий источник пропитания, и один вид может пожирать другой, как в примере с львами и гиенами, где они могут также убивать друг друга.
Модели конкуренции не ограничиваются биологией и экологией. Страны конкурируют между собой за владение большей долей в торговле товарами и услугами, корпорации и фирмы конкурируют за клиентов и долю на рынке, политические партии борются за голоса. Также новые технологии и инновационные решения конкурируют за доступ и открытие новых рынков и распространение на существующих рынках, где, как правило, доминируют существующие старые и сильные технологии и компании.
Итак, в данной модели имеются три вида объектов, сосуществующих и взаимодействующих друг с другом [1, 2]:
а) корпорации-хищники, которые являются большими и успешными компаниями, но имеют свои уязвимые аспекты и упущения, которые они хотят восполнить путем поглощения другой, более мелкой компании;
б) «жертвы» представлены малым бизнесом – стартапами и МИПами. «Жертвы», как правило, незрелые компании, находящиеся в сегменте малого и микро-бизнеса. Они имеют свои сферы специализации, в которых достигли значительного успеха с точки зрения эффективности. Также «жертвы» должны иметь цену продажи достаточно низкую для возможности покупки «хищниками»;
в) государственный регулятор, выраженный в накопленном налоге, который занимается перераспределением средств в данной системе: он облагает «хищников» налогами, таким образом формируя бюджет, из которого осуществляется поддержка малого бизнеса (стартапов и МИПов) в виде дотаций.
Данная модель предполагает наличие специализированного реестра или базы данных малого бизнеса, из которых «хищники» выбирают себе наиболее пригодных «жертв» [5].
Графически данная модель отображена в виде диаграммы причинно-следственных связей, изображенной на рис. 2.
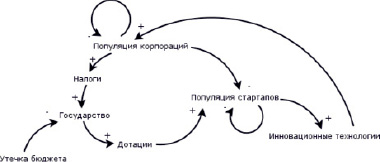
Рис. 2. Причинно-следственные связи в инновационной экосистеме
Модернизируем модель с учетом ряда поправочных коэффициентов [4, 6].
Модели Лотки – Вольтерры были модернизированы следующим образом:
1) государство может облагать налогом корпорации (τ) для пополнения бюджета страны;
2) в связи с чем добавляется переменная T, которая вычисляется через дополнительное дифференциальное уравнение;
3) бюджет (T) накапливается благодаря налогам, собранным с корпораций (y∙τ);
4) часть бюджетных денег тратится на дотации «стартапам» (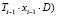 ;
;
Математически данная модель выражена следующим образом:
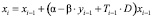 ,
,
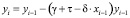 ,
,
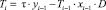 ,
,
x – количество МИПов,
y – количество корпораций,
i – период моделирования,
α – коэффициент рождаемости стартапов,
β – коэффициент поглощения стартапов корпорациями,
γ – коэффициент смертности корпораций,
δ – коэффициент рождаемости корпораций,
τ – налоговая ставка для корпораций,
T – собранные налоги за данный период,
D – дотационная доля бюджета на помощь «стартапам».
Для реализации математической модели (формула выше) была разработана имитационная модель в среде моделирования Anylogic (рис. 3).
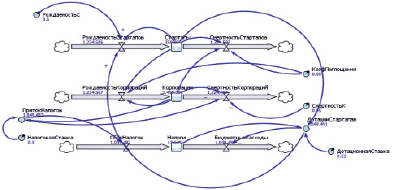
Рис. 3. Диаграмма потоков и накопителей
В данной среде был проведен оптимизационный эксперимент (рис. 4) с автоматическим подбором параметров, приведенных в табл. 2, максимизирующий накопленные значения переменных x и y за все периоды с ограничениями: значения этих переменных не должны быть меньше начальных (xнач = 100 и yнач = 50.
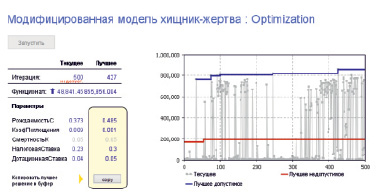
Рис. 4. Оптимизационный эксперимент
Таблица 2
Варьирование параметров при оптимизации и оптимизированные параметры
|
Параметр |
Минимальное значение |
Максимальное значение |
Шаг |
Оптимизированные параметры |
|
Рождаемость «стартапов» |
0,001 |
0,5 |
0,001 |
0,485 |
|
Коэффициент поглощения |
0,001 |
0,5 |
0,001 |
0,009 |
|
Налоговая ставка |
0,01 |
0,3 |
0,01 |
0,5 |
|
Дотации |
0,01 |
0,5 |
0,01 |
0,05 |
Равновесие достигается выбором определенного значения параметра, определяющего уровень налогов, собираемых с корпораций (τ), которые впоследствии будут отчислены в пользу «стартапов», а также соответствующего параметра, определяющего уровень субвенций «стартапам» на каждом шаге (D), см. рис. 5.
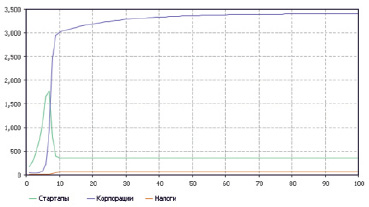
Рис. 5. Поведение системы при оптимизированных параметрах
Учитывая, что данная модель является сильно абстрагированной, не учитывает наличие жизненного цикла развития инновационной идеи, индивидуального поведения и не позволяет сделать конкретные практические выводы применительно к экономике, для более детального определения параметров эффективного взаимодействия, необходимо прибегнуть к созданию многоагентной имитационной модели, моделирующей взаимоотношения «стартапов», венчурных инвесторов и корпораций, что будет описано в следующей части статьи.
Выполнено в рамках научно-исследовательской работы по гранту Президента РФ МК-6249.2016.9 для государственной поддержки молодых российских ученых (Конкурс – МК-2016).
Библиографическая ссылка
Ахмадеев Б.А., Вейнберг Р.Р., Титов В.А. РЕАЛИЗАЦИЯ МОДЕРНИЗИРОВАННОЙ МОДЕЛИ «СТАРТАП, ИНВЕСТОР-КОРПОРАЦИЯ И ГОСУДАРСТВО» В СИСТЕМЕ ANYLOGIC // Фундаментальные исследования. 2017. № 8-1. С. 115-119;URL: https://fundamental-research.ru/ru/article/view?id=41631 (дата обращения: 07.03.2026).



