Компьютерное моделирование динамического поведения сложных технических устройств – мощное средство выявления рациональной кинематической схемы и эффективных алгоритмов управления проектируемых механизмов. Часто только с помощью моделирования можно получить ответы на вопросы, возникающие на всех этапах разработки, испытаний технических устройств, а также в процессе их эксплуатации. Компьютерное моделирование позволяет сократить время и стоимость новых разработок.
На стадии проектирования в качестве математической модели технического устройства часто используют систему связанных абсолютно твёрдых тел. Разнообразие возможных конструкций, сложность математического описания движения многосвязной системы делают актуальным создание системы автоматизированного составления математической модели и компьютерного моделирования функционирования механической системы с заданной кинематической схемой. Использование для этих целей классических подходов теоретической механики (например, уравнений движения в форме Лагранжа второго рода) приводит к созданию программ моделирования, требующих значительной оперативной памяти и высокого быстродействия ЭВМ.
В статье предлагается метод моделирования на ЭВМ динамики голономных механических систем большой размерности, расчётная схема которых может быть представлена в виде связки абсолютно твёрдых тел со структурой дерева, без явного формирования уравнений движения в виде системы дифференциальных уравнений.
Уравнения движения системы связанных твёрдых тел
Рассмотрим систему связанных абсолютно твёрдых тел со структурой дерева. Способы соединения тел определяются уравнениями связи. Будем предполагать, что кинематические связи, реализуемые в соединениях, голономны и идеальны.
Пусть N – число тел в системе (не считая тела «0», движение которого относительно инерциальной системы координат Oxyz задано функцией времени). Остальным телам системы присвоим номера таким образом, чтобы для любого тела номер предшествующего ему тела был меньше. Для полного описания структуры взаимосвязей в системе достаточно одного целочисленного массива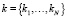 
, на i-м месте которого расположен индекс тела, предшествующего i-му. Массив k позволяет определить для каждого тела системы целочисленные массивы Si номеров тел, для которых i-е тело является предшествующим.
Обозначим через Oi полюс ортогональной декартовой системы координат, связанной с телом. Положение i-го тела в пространстве относительно базового для него ki-го тела полностью определяется матрицей-столбцом ρi, элементами которой являются проекции вектора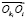 
на оси системы координат, связанной с телом ki и матрицей Gi направляющих косинусов между базисными векторами, связанными с телами ki и i. Абсолютную скорость каждого тела зададим 6-мерной матрицей-столбцом νi = (ωi, νi)T, где ωi, νi – векторы мгновенных угловой и линейной скоростей i-го тела. Аналогично, абсолютное ускорение каждого тела системы определим с помощью 6-мерной матрицы-столбца wi = (εi, wi)T, где εi, wi – мгновенные угловое и линейное ускорения i-го тела. Векторы νi, ωi, wi и εi будем задавать в системе координат, связанной с телом.
Для каждого соединения тел в соответствии с видом уравнений связи введём матрицу-столбец локальных обобщённых координат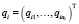 
(ni ≤ 6). Тогда элементы матриц ρi и Gi будут являться в общем случае функциями времени и выбранных координат относительного движения. В качестве обобщённых параметров системы примем совокупность 
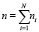локальных обобщённых координат 
.
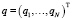Принимая движение i-го тела за относительное, а предшествующего ему ki-го тела за переносное, можно записать рекуррентные формулы для вычисления скоростей и ускорений тел механической системы [1]:
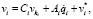(1)
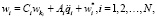(2)
где матрицы Ci имеют вид
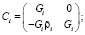
Ai – матрицы локального касательного базиса многообразия относительного движения в i-м сочленении;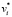 
– матрицы-столбцы составляющих относительных скоростей тел системы, не зависящих от обобщённых скоростей 
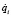; а в матрицы-столбцы 
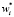вошли все члены переносного, кориолисова и относительного ускорений. Здесь и далее символ «∼» используется для обозначения кососимметричной матрицы [2].
Обозначим через fi и μi главный вектор и главный момент активных сил, действующих на i-е тело. Уравнения движения выпишем в форме уравнений Ньютона – Эйлера для свободного твёрдого тела 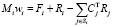[3]:
(3)
со следующими матрицами
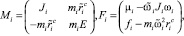
где mi – масса i-го тела, Ji – тензор инерции i-го тела в связанной с телом системе координат,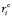 
– радиус-вектор центра масс i-го тела в связанной с ним системе координат, Ri – матрица-столбец реакции связей в i-м сочленении, 
.
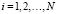Уравнения (2) и (3) замыкаются соотношениями
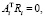(4)
отражающими то обстоятельство, что при идеальности связей в сочленениях реакции являются ортогональными к конфигурационному многообразию относительных положений, определяемому параметрами qi. Таким образом, получается замкнутая система 12N + n скалярных дифференциальных и алгебраических уравнений (2)–(4) относительно такого же количества неизвестных величин wi, Ri и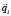 
.
При интегрировании уравнений движения на ЭВМ численными методами необходимо на каждом шаге один или несколько раз вычислять ускорения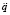 
при заданных координатах q и скоростях 
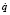. В нашем случае определение ускорений 
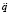сводится к простой алгебраической задаче решения системы линейных уравнений (2)–(4) с учётом соотношений (1).
Запишем систему уравнений (2)–(4) в виде единого матричного уравнения. Для системы тел, имеющей структуру цепочки, оно будет иметь следующий вид:
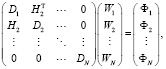(5)
где
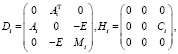
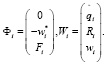
Нетрудно видеть, что матрица системы (5) является симметричной и имеет блочную трёхдиагональную структуру, которую можно эффективно использовать.
Разрешение уравнений движения методом прогонки
Метод прогонки тел по существу является модификацией метода Гаусса решения систем линейных алгебраических уравнений с ленточной структурой. В данном методе при прямом ходе, который выполняется начиная с последнего тела системы, из группы уравнений (3) исключаются реакции связей носимых тел. При обратном ходе по явным формулам вычисляются последовательно для каждого тела системы обобщённые ускорения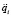 
, декартовые ускорения wi и реакции связей Ri.
Суть метода подробно изложена в статье [4]. Здесь же приведём только алгоритм метода прогонки, обобщённый на случай систем тел со структурой дерева:
for i = N:1
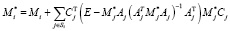
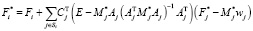
end
for i = 1: N
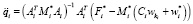
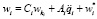
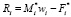
end
Трудоёмкость вычислений по указанным рекуррентным формулам линейно растёт с ростом числа тел в системе. При этом в алгоритме требуется обращение симметричных положительно определённых матриц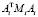 
, порядок которых равен числу степеней свободы в i-м сочленении, т.е. не превышает шести. Этим и обуславливается высокая эффективность описанного выше алгоритма разрешения уравнений движения относительно ускорений.
Впервые подобные формулы были получены А.Ф. Верещагиным в 1974 г. [5] для пространственных механизмов, содержащих ряд звеньев, соединённых в цепь с одной степенью подвижности между звеньями.
Разрешение уравнений движения с помощью блочного LTDL-разложения
Идея исключения Гаусса – это преобразование исходной системы уравнений в эквивалентную треугольную систему с последующим её решением. В матричном виде это есть LU-разложение [6]. В случае симметричной матрицы системы уравнений (5) лучше использовать LTDL-разложение. Заметим, что при разложении ленточных систем треугольные множители L также являются ленточными.
Первый шаг алгоритма блочного LTDL-разложения, применённого к блочной трёхдиагональной матрице системы (5), можно записать в виде
со следующими матрицами
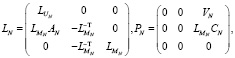
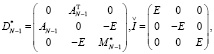
где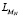 
и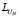 
– факторы Холецкого симметричных положительно определённых матриц VN и 
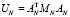соответственно, матрица VN находится из матричного уравнения 
,
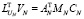а матрица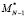 
вычисляется по формуле 
.
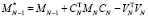Нетрудно видеть, что матрица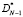 
имеет ту же структуру, что и матрица DN, и, следовательно, процесс разложения матрицы 
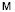на множители можно продолжить:
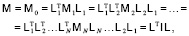
где
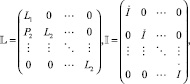
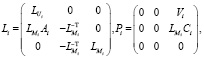
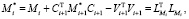
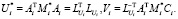
После того как матрица коэффициентов системы уравнений (5) разложена на произведение треугольных матриц, для нахождения решения этой системы необходимо последовательно решить две системы уравнений с треугольными матрицами:
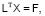(6)
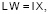(7)
где
, 
,
,
.
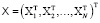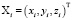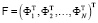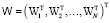Решая систему (6), начиная с последнего уравнения, получим
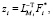
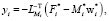
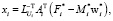
где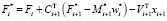 
.
Решая систему (7) и исключая переменные zi, yi, получим
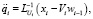
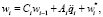
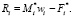
Обобщая полученные формулы на случай системы твёрдых тел со структурой дерева, можно записать следующий алгоритм решения расширенной системы уравнений (2)–(4):
for i = N:1
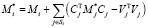
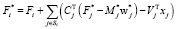
Найти фактор Холецкого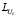 
матрицы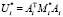 
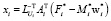
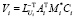
end
for i = 1: N
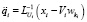
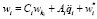
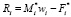
end
Нетрудно видеть, что в полученном алгоритме, как и в алгоритме, основанном на методе прогонки, трудоёмкость вычислений растёт линейно с ростом числа тел в системе, но вместо обращения матриц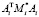 
обращаются их факторы Холецкого, которые являются треугольными матрицами. Поэтому трудоёмкость разрешения уравнений движения относительно обобщённых ускорений полученным алгоритмом оказывается ниже, чем в методе А.Ф. Верещагина.
Сравнение методов по эффективности
Приступая к сравнению рассмотренных выше методов разрешения системы дифференциально-алгебраических уравнений движения относительно ускорений, заметим, что метод прогонки неявно вычисляет LU-разложение матрицы системы. Это разложение не учитывает симметричность матрицы системы и, как известно, по числу арифметических операций практически в два раза уступает методу Холецкого, учитывающего эту особенность матрицы.
При численном интегрировании дифференциальных уравнений движения механических систем вычислительные затраты можно разделить на затраты собственно метода интегрирования и на затраты, связанные с вычислением правых частей. Вычисление правых частей системы уравнений, то есть фактически вычисление обобщённых ускорений, можно разделить на две подзадачи. Первая – по известным обобщённым координатам и скоростям вычисляются скорости тел и силы, действующие на них. Вторая – разрешение уравнений движения относительно обобщённых ускорений.
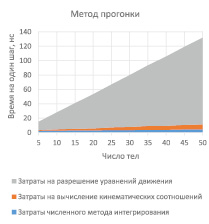
Сравнение алгоритмов разрешения уравнений движения проводилось с помощью компьютерного моделирования динамики механических систем, представляющих собой цепочки твёрдых тел, соединённых трёхстепенными шаровыми шарнирами. При сравнении варьировалось число тел в цепочке. Дифференциальные уравнения решались методом Штёрмера [7] с порядком аппроксимации равным шести. Эффективность методов измерялась временем выполнения одного шага этого численного метода.
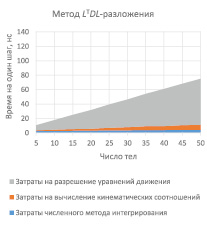
На рис. 1 и 2 представлены зависимости затрат времени на выполнение одного шага интегрирования от числа тел в цепочке для рассматриваемых методов разрешения уравнений движения.
а) б)
Рис. 1. Зависимость затрат времени на выполнение одного шага интегрирования от числа тел в цепочке для рассматриваемых методов разрешения уравнений движения
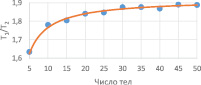
Рис. 2. График отношения T1/T2
Анализ этих зависимостей подтверждает теоретические расчёты. Видно, что затраты времени растут линейно от числа тел в системе. Причём затраты времени на разрешение уравнений движения относительно ускорений занимают львиную долю всех временных затрат.
Для сравнительной оценки эффективности методов построим график отношения T1/T2 (рис. 2), где T1 и T2 – временные затраты на разрешение уравнений движения методом прогонки и методом LTDL-разложения соответственно.
Нетрудно видеть, что метод, основанный на симметричном LTDL-разложении, эффективнее метода прогонки, не учитывающего особенности уравнений движения системы тел. Из рис. 3 видно, что алгоритм LTDL-разложения в 1,6–2 раза сокращает временные затраты на разрешение уравнений движения по отношению к методу прогонки.
Заключение
Предложен новый рекуррентный алгоритм разрешения уравнений движения систем связанных твёрдых тел со структурой дерева относительно ускорений при их численном интегрировании. Проведено сравнение предложенного алгоритма с классическим алгоритмом метода прогонки А.Ф. Верещагина, имеющим тот же порядок вычислительной сложности. На примерах моделирования механических систем с различным числом степеней свободы показано, что предложенный алгоритм быстрее классического более чем в полтора раза.
Библиографическая ссылка
Шимановский В.А. МЕТОД КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ДИНАМИКИ СИСТЕМ СВЯЗАННЫХ ТВЁРДЫХ ТЕЛ // Фундаментальные исследования. – 2017. – № 8-1. – С. 104-109;URL: https://fundamental-research.ru/ru/article/view?id=41629 (дата обращения: 09.10.2024).