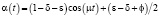Дифференциальные уравнения дробных порядков представляют большой интерес для исследования, так как часто находят свое применение во многих областях науки, таких как: математика, физика и др. [1, 2]. Уравнения с дробными производными принадлежат классу интегро-дифференциальных уравнений и называются по терминологии В. Вольтерра эредитарными [3]. Данное понятие означает наличие в изучаемом процессе эффекта памяти и характеризуется ядром интегро-дифференциального уравнения – функцией памяти. Если функция памяти является степенной, то мы естественным образом переходим к уравнению с дробной производной, которое изучается в рамках дробного исчисления [4, 5]. Одним из таких уравнений является эредитарное уравнение Риккати [6–8].
В работах [6–8] эредитарное уравнение Риккати было решено численно с помощью аппроксимации дробной производной конечной разностью. Далее реализация численного алгоритма сводилась к решению системы квадратных уравнений. Выбирая порядок дробной производной как некоторую функцию от времени, построим семейство расчетных кривых, а также фазовые траектории. Были получены новые режимы распределений, которые зависят от конкретного вида переменного порядка дробной производной. Показано, что некоторые кривые распределений характерны для других эредитарных динамических систем. Также был исследован численный метод на погрешность с помощью правила Рунге.
В настоящей работе для автоматизации расчетов была разработана программа «NSFDRE» на языке C++ для численного решения уравнения Риккати с дробной производной переменного порядка. В программе реализован численный алгоритм расчета, а также предусмотрена возможность визуализации результатов расчета.
Материалы и методы исследования
Рассмотрим следующее эредитарное уравнение:
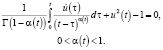 (1)
(1)
где 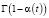 – гамма-функция Эйлера. Для уравнения (1) введем следующее обозначение:
– гамма-функция Эйлера. Для уравнения (1) введем следующее обозначение:
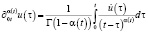 , (2)
, (2)
которое является обобщением дробного оператора Герасимова – Капуто [9]. Необходимо отметить, что существуют другие определения производной дробного переменного порядков [9]. Мы же остановимся на определении (2), так как для уравнения (1) в компактной форме
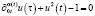 , (3)
, (3)
справедливо начальное условие:
u(0) = φ, (4)
где φ – const. Уравнение (3) является аналогом классического уравнения Риккати [10] и учитывает эффект памяти. Вследствие вышесказанного постановка задачи для эредитарного уравнения Риккати (1) в данном случае свелась к задаче Коши (3) и (4). Заметим, что в случае, когда α(t) – const, мы приходим к задаче Коши, рассмотренной в работе [11], если α(t) = 1, то задача Коши (3) и (4) переходит в классическую задачу Коши для уравнения Риккати.
Задача Коши (3) и (4) в общем случае не имеет точного решения, поэтому мы будем использовать численные методы для ее решения. Для этого разобьём временной отрезок 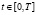 на N равных частей, где τ = T/N – шаг дискретизации, и получим что tn = nτ,
на N равных частей, где τ = T/N – шаг дискретизации, и получим что tn = nτ, 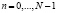 а функция решения u(tn) = un. Аппроксимацию дробной производной (2) проведем согласно работам [13, 14] в виде
а функция решения u(tn) = un. Аппроксимацию дробной производной (2) проведем согласно работам [13, 14] в виде
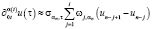 ,
,
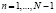 , (5)
, (5)
где весовые коэффициенты равны
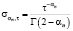 ,
,
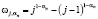 .
.
Можно показать, что аппроксимация (5) имеет первый порядок. Интегро-дифференциальную задачу Коши (3) и (4) можно переписать в разностной постановке:
 , u0 = ρ. (6)
, u0 = ρ. (6)
Мы получили систему нелинейных алгебраических уравнений, алгоритм решения которой был реализован в программе NSFDRE. Численное решение производилось особым образом, суть которого в том, чтобы свести вычисление значения функции в каждом узле сетки к решению квадратного уравнения (6). Алгоритм приведен на блок-схеме (рис. 1).
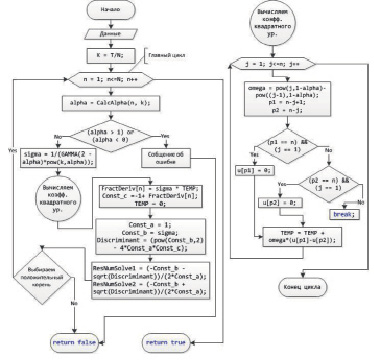
Рис. 1. Блок-схема класса для численного решения
Заметим, можно было использовать для численного решения метод Ньютона или Pade-аппроксимации, как, например, в работе [11]. Однако указанные методы требуют больше машинного времени и памяти для решения. Поэтому был выведен и использован именно такой способ решения. На рис. 2 приведена главная форма программы для ввода параметров задачи.
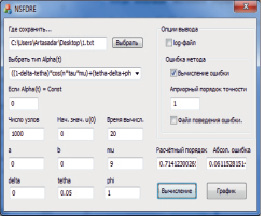
Рис. 2. Введение параметров на главной форме программы NSFDRE
Результаты исследования и их обсуждение
Рассмотрим некоторые примеры.
Пример 1. Рассмотрим пример, где α(t) = const, уже исследованный в работе [11]. Значения управляющих параметров выберем следующими: 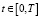 , T = 3, N = 1000, τ = 0,003, φ = 0,2.
, T = 3, N = 1000, τ = 0,003, φ = 0,2.
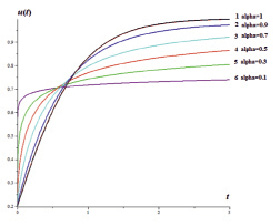
Рис. 3. Семейство расчетных кривых, полученных из решения системы (6) для различных значений дробного параметра α
На рис. 3 приведено семейство расчетных кривых задачи Коши (3) и (4) в зависимости от значений дробного параметра α: α = 1 (кривая 1 – соответствует классическому решению уравнения Риккати), α = 0,9 (кривая 2), α = 0,7 (кривая 3), α = 0,5 (кривая 4), α = 0,3 (кривая 5), α = 0,1 (кривая 6). Заметим, что при уменьшении значения дробного параметра α, в исходном уравнении, приводит к перестройке расчетных кривых численных решений задачи Коши (3) и (4). Это связано с тем, что наличие эффекта памяти в изучаемом процессе будет приводить к «тяжелым затягивающимся хвостам» в кривых распределений полученных решений. Если среда обладает эффектами памяти, то иногда такую среду называют фрактальной, а дробный параметр α связан с ее характеристикой – фрактальной размерностью среды. Поэтому исследование параметра α имеет важное значение для различных приложений, где изучаются свойства среды или материалов.
Пример 2. Рассмотрим другой пример, когда α(t) – является некоторой периодической функцией. Пусть
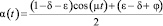 ,
,
тогда, положив значения управляющих параметров равными: δ = 0, ε = 0,05, μ = 9, φ = 1, 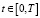 , T = 20, N = 1000, τ = 0,02, ρ = 0, получим следующие результаты, приведенные на рис. 4.
, T = 20, N = 1000, τ = 0,02, ρ = 0, получим следующие результаты, приведенные на рис. 4.
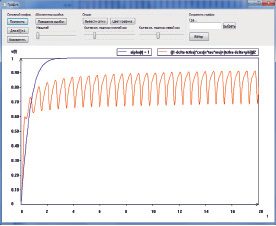
Рис. 4. Расчётные кривые: синяя – классическое решение α(t) = 1; красная – кривая численного решения системы (8)
Из результатов моделирования, приведённых на рис. 4, можно сделать вывод о том, что если выбрать параметр α(t) в виде периодической функции, в данном случае тригонометрической, то решение задачи Коши (3) и (4) будет описывать колебательный режим. Колебательный режим, приведенный на рис. 4 (красная кривая), похож на один из колебательных режимов автогенератора Ван дер Поля [14–16], что имеет большой практический интерес при моделировании нелинейных осцилляторов. Из рис. 4 видно, что колебания происходят сначала с возрастанием амплитуды, потом амплитуда устанавливается. Действительно, этот факт хорошо виден на рис. 4.
Фазовая траектория рис. 5 выходит на предельный цикл, напоминающую петлю гистерезиса. Этот пример показывает, что с помощью эредитарного уравнения Риккати с переменным дробным порядком производной можно моделировать различные колебательные режимы.
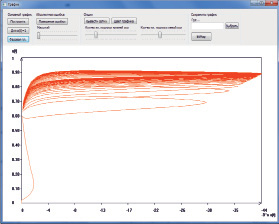
Рис. 5. Фазовая траектория
Исследование на погрешность метода
Рассмотрим изменение абсолютной ошибки ε и расчётный порядок точности 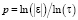 схемы (6), при изменении шага τ. Для вычисления абсолютной ошибки ε будем использовать правило Рунге [17]:
схемы (6), при изменении шага τ. Для вычисления абсолютной ошибки ε будем использовать правило Рунге [17]:
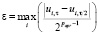 ,
,
где 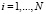 .
.
Априорную точность paprior решения в данном методе положим равной 1. Это следует из общего порядка аппроксимации схемы, задаваемого в граничных узлах сетки.
Результаты исследования численной схемы (8) на ошибку и точность
|
N (кол. узлов) |
τ = T/N (шаг) |
ε (ошибка) |
p (точность) |
|
Пример 1. α(t) = 0,9999 |
|||
|
65 |
0,04615 |
0,0080057826 |
1,569552780 |
|
131 |
0,02290 |
0,0040108135 |
1,461309925 |
|
263 |
0,01141 |
0,0020088245 |
1,388207803 |
|
527 |
0,005693 |
0,0010069838 |
1,335141320 |
|
1055 |
0,002844 |
0,0005117944 |
1,292511738 |
|
2111 |
0,001421 |
0,0002509894 |
1,264446995 |
|
Пример 2. |
|||
|
65 |
0,3077 |
– |
– |
|
131 |
0,1527 |
0,157214319 |
0,9843999572 |
|
263 |
0,07605 |
0,093047735 |
0,9216824185 |
|
527 |
0,03795 |
0,047894435 |
0,9288660948 |
|
1055 |
0,01896 |
0,024516910 |
0,9351487980 |
|
2111 |
0,009474 |
0,01227877 |
0,9443462189 |
Из таблицы следует, что абсолютная ошибка ε уменьшается примерно в два раза при уменьшении шага τ также в два раза. В обоих случаях ошибка будет уменьшаться пропорционально уменьшение шага. Расчётный порядок точности p в первом случае ожидаемо стремится к 1. Во втором же случае порядок точности при малых N уменьшается, однако при N > 236 вновь начинает расти, как видно из таблицы, и вероятно так же будет стремиться к 1. Такое поведение, возможно, объясняется свойствами логарифма при вычислении p.
Заключение
Введение дополнительного дробного параметра α(t) в уравнение Риккати приводит к появлению новых кривых распределений, которые характеризуют решение задачи Коши (3) и (4), вследствие чего можно моделировать колебательные режимы и строить модели различных сигналов, это несомненно заслуживает внимания для решения прикладных задач. Результаты исследования абсолютной ошибки и расчётного порядка точности для примера 1 и примера 2 позволяют предположить, что численная схема (6) применима к данной задаче. Возможное продолжение исследования эредитарного уравнения Риккати (1) связано с прикладными задачами, например, в экономике [18, 19], а также в решении обратной задачи оценки параметра α(t) по экспериментальным данным.
Работа выполнена по госзаданию КамГУ имени Витуса Беринга, НИР «Применение дробного исчисления в теории колебательных процессов» № AAAA-A17-117031050058-9.
Библиографическая ссылка
Твердый Д.А., Паровик Р.И. ПРОГРАММА ЧИСЛЕННОГО РАСЧЕТА ЗАДАЧИ КОШИ ДЛЯ УРАВНЕНИЯ РИККАТИ С ПРОИЗВОДНОЙ ДРОБНОГО ПЕРЕМЕННОГО ПОРЯДКА // Фундаментальные исследования. 2017. № 8-1. С. 98-103;URL: https://fundamental-research.ru/ru/article/view?id=41628 (дата обращения: 07.03.2026).