В связи с развитием технических устройств беспроводной передачи сигналов в настоящее время становится актуальной разработка мобильных устройств дистанционного мониторинга физиологических параметров, например [10–12]. В качестве целевого назначения таких устройств могут быть: проведение научных исследований, разработки перспективных мобильных медицинских устройств мониторинга состояния биообъекта, а также разработка массовых персональных устройств мониторинга определенных физиологических показателей. Однако при разработке таких устройств ключевой проблемой становится разработка эффективных алгоритмов анализа снимаемых сигналов для выделения информативных составляющих с целью последующего распознавания, оценки или диагностики состояния биообъекта. Такое требование обусловлено существующими ограничениями энергетических и вычислительных ресурсов мобильных устройств. Кроме этого, поскольку снимаемые сигналы имеют аналоговую природу, а устройства обработки – цифровую, то возникают разные варианты размещения аналого-цифрового преобразователя в канале передачи –приема сигнала [1].
Существующие решения
Для передачи информации в настоящее время используются различные каналы, информация в которых передается в модулированном виде. При этом наибольший практический интерес представляют помехозащищенные каналы. Известно, что помехозащищенность и селективность достигается модуляцией информационного сигнала несущей. В настоящее время наиболее изучены несколько видов модуляции: аналоговая модуляция (АМ), частотная модуляция (ЧМ) и фазовая модуляция (ФМ), а также их комбинированные и специальные виды [1]. Кроме этого также используют цифровую модуляцию как аналогового, так и цифрового сигнала, при этом в общем случае говорят о манипуляции сигналом.
Для получения исходного сигнала модулированный сигнал демодулируют (производят обратное преобразование). Как правило, демодуляцию производят с помощью аналоговых устройств собранных на основе чувствительных элементов к изменению того или иного параметра (реактивных элементов – индуктивности, конденсатора). Основным недостатком таких решений является их сложность в настройке и высокая стоимость.
При применении в цифровых устройствах используются прямые цифровые аналоги аналоговых схем [2]. Среди алгоритмов, используемых для цифровой демодуляции и выявления параметров сигнала, наиболее часто применяются:
1. CORDIC (COordinate Rotation DIgital Computer) [7].
2. Квадратурный приемник [9].
3. Схема Костаса [9].
Все цифровые схемы сводятся к использованию квадратурного приемника и вычисления с помощью него параметров сигнала: синфазной составляющей и квадратурной составляющей. Таким образом, цифровые программные решения являются, как правило, ресурсозатратными с точки зрения вычислительной мощности. В условиях, когда аналоговый сигнал в обязательном порядке принимает дискретную форму, отсутствуют веские основания рассматривать его обработку с помощью аналоговых схем. Следовательно, наиболее эффективной с точки зрения авторов является работа с сигналом в цифровом виде и численные методы его обработки.
Постановка задачи
Таким образом, ставится задача разработки метода и алгоритма демодуляции сложного по составу периодического сигнала для выделения информативных составляющих и их параметров, позволяющего использовать его во встроенных системах с небольшими вычислительными ресурсами.
Предлагаемое решение
Поставленная задача вычислений при ограниченных ресурсах в наиболее явном виде решается в природе. Способ построения вычислений показан в работе Бакусова и др. [6], где вводится понятие биопроцессор. Отметим, что биопроцессор можно рассматривать как считающую структуру данных, которая эффективно воспроизводит как заданную последовательность в инвариантном масштабе (биопроцессор с Лагранжевой структурой), так и располагает анализирующими свойствами – разложением двухмерного сигнала (гармонического sin(x), x) в 4-мерное пространство (cos(x), sin(x), cons(x), x) при использовании одной гармоники для анализа. Таким образом, анализирующий биопроцессор преобразует в результате вычислений исходный сигнал в 4-х мерное пространство в соответствии с заданными параметрами.
Для анализа сигнала был выбран наиболее компромиссный метод модуляции по затратам вычисления и помехоустойчивости – фазовая модуляция [1, 2, 9]. При фазовой модуляции сигнал имеет вид
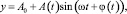 (1)
(1)
где j(t) – функция изменения фазы, или, в нашем случае, информационный сигнал.
Имея интерполирующий полином Гаусса [3, 4, 8]:
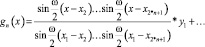
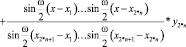 , (2)
, (2)
где n – число гармоник сигнала в окне интерполяции.
Возьмем одну гармонику и построим для нее интерполяционный многочлен:
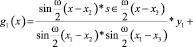
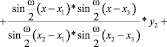
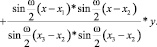 (3)
(3)
При перегруппировке каждого из членов (разложении умножения синусов) получаем
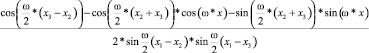
для первого члена и т.д. для последующих.
При перегруппировке получаем коэффициенты:
1) перед const:
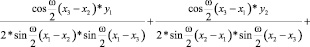
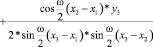 , (4)
, (4)
2) перед cos(wx)
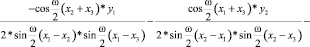
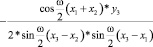 , (5)
, (5)
3) перед sin(wx)
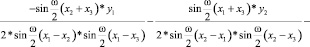
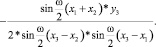 (6)
(6)
При подстановке sin в формулы получаем следующий вектор значений (С_const, С_cos, С_sin) – (0, 0, 1). При подстановке 3 + 2sin – (3, 0, 2). И при sin (x + 2p45/180) – (0, 0,71, 0,71).
Такие значения имеют место в «окне интерполяции» (рис. 1), то есть в тех трех точках, представленных интерполяционным многочленом. Интерес представляют динамические параметры «свертки» сигнала процессором во времени – т.е. при «скольжении» окна по сигналу вдоль временной оси.
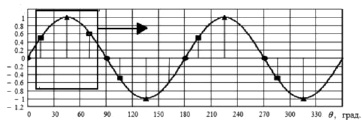
Рис. 1. Пример движения окна интерполяции процессора, построенного для одной гармоники
Основным случаем свертки сигнала при вышеописанных условиях является свертка сигнала представленного одной гармоникой, частота которой равна частоте процессора:
yi = sin(ωxi + φ(i)). (7)
Положим для простоты, что счет времени представлен натуральным рядом, т.е. в масштабе сигнала:
x1 = ∆x; x2 = 2∆x; x3 = 3∆x; …xn = n∆x; k = ((ω∆x))/2.
Отсчеты в окне возьмем симметрично его середине:
x1окна = ∆x(i – 1); x2окна = ∆xi; x3окна = ∆x(i + 1);
где i – отсчет в центре окна.
При свертке сигнала с коэффициентом перед sin(wx) получаем выражение (8).
При подстановке j(i – 1) = j(i) =
= j(i + 1) = const формула сворачивается до cos(j(i)). Из выведенных соотношений следуют две особенности рассматриваемой схемы: при больших скоростях роста фазы в свертке (8) появляется помеха, влияющая на форму сигнала; результирующий вектор представляет собой полный ортогональный базис гармонического сигнала. Из этого следует, что A = sqrt(C_sin^2 + C_cos^2); phase = arccos(С_sin/A).

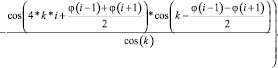 (8)
(8)
Экспериментальная проверка
Для проверки работоспособности и эффективности биопроцессора Бакусова был проведен математический эксперимент. В эксперименте основной формой сигнала являлся синусоидальный сигнал с базовой частотой, на распознавание которой настроен анализирующий процессор. Были использованы три способа изменения фазы: фаза являлась константой, линейное нарастание фазы без помех и линейное нарастание фазы в условиях белого шума с отношением сигнал/шум равным 60 дБ. Стоит упомянуть, что также возможны другие варианты фазовой модуляции (более сложные p(x)), но в таком случае изменяется вид ошибки процессора – это выражается во влиянии скорости роста фазы на результат вычисления координат 4-мерного вектора.
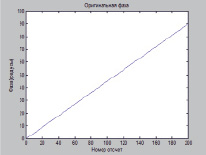
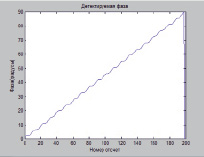
Рис. 2. Фаза сигнала и детектируемая фаза для сигнала с нарастающей фазой без помехи
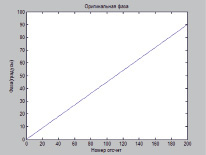
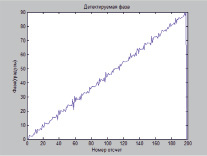
Рис. 3. Фаза сигнала и детектируемая фаза сигнала с нарастающей фазой и помехой вида «белый шум»
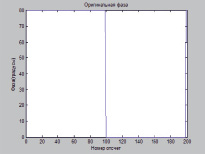
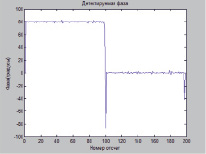
Рис. 4. Фаза сигнала и детектируемая фаза сигнала вида «ступенчатое воздействие»
и помехой вида «белый шум»
На рис. 2 представлен пример с линейным трендом роста фазы от 0 до 80 градусов.
На рис. 3 представлен сигнал с линейным трендом роста фазы и помехой (отношение сигнал/шум равно 60 дБ) на формирование фазы.
На рис. 4 представлена фазовая манипуляция сигналом с помехой в передающем канале (отношение сигнал/шум равно 60 дБ).
Очевидно, что фаза сигнала содержит ошибку вычисления и набегающую ошибку. Ошибка вычисления связана с конечной точностью представления чисел. Набегающая ошибка связана с высокочастотной составляющей в многочленах, выражающих синус и косинус, а также с помехами, накладываемыми на сигнал в тракте передачи.
Выявленная особенность будет сказываться при длительных циклах передачи и несущественна при пакетном режиме передачи, который используется в сотовой телефонии. Таким образом, несмотря на наличие таких помех, предложенная методика в целом вполне пригодна для манипуляции сигнала в многосимвольном режиме [5]. С этой же точки зрения стоит оценивать и эффективность алгоритма перед его аналогами.
Заключение
Разработан новый подход к обработке периодического сигнала, который в силу своей вычислительной простоты (вычисления несут рекурсивный характер, обусловленный постоянным приращением угла во время движения окна) может быть применен как во встраиваемых системах, так и в носимой электронике. Также такой метод может применяться для обработки массивов аналоговых данных, имеющих большую размерность. Была оценена практическая сторона применения метода обработки в виде эксперимента с цифровым каналом связи. Определено, что имеющийся тренд изменения фазы позволяет определять параметры сигнала в режиме пакетной передачи данных.
Библиографическая ссылка
Кружков А.С., Насыров Р.В. ПРИМЕНЕНИЕ АНАЛИЗИРУЮЩЕГО ПРОЦЕССОРА ДЛЯ ЦИФРОВОЙ ДЕМОДУЛЯЦИИ АНАЛОГОВОГО СИГНАЛА НА ОСНОВЕ БИОНИЧЕСКОГО ПОДХОДА // Фундаментальные исследования. 2017. № 8-1. С. 49-54;URL: https://fundamental-research.ru/ru/article/view?id=41619 (дата обращения: 07.03.2026).
DOI: https://doi.org/10.17513/fr.41619



