В работе [1] рассматривалась проблематика моделирования динамики «затраты – выпуск» для предприятия с неоклассической производственной функцией. Применив аппарат линейных разностных уравнений второго порядка, авторы вывели конечное выражение для выпуска предприятия и оценили результаты влияния эндогенных параметров модели γt и βt (доли соответственно собственных инвестиций в конечном продукте предыдущего планового периода и заемных средств в совокупных инвестициях производственной сферы текущего периода) на качество принимаемых в этой сфере решений [5]. Были также проведены расчеты влияния структуры рабочего капитала, авансируемого в покрытие затрат производственной деятельности, на финансовые результаты. Кроме того, авторы установили, что масштаб производства (степень однородности производственной функции) является основным экзогенным параметром, а в сочетании с управляемыми параметрами γt и βt на его основе можно определить величину денежных и материальных потоков и рассчитать экономическую динамику производственной сферы предприятия с учетом эффектов финансового и операционного рычагов.
Однако в приведенной выше и аналогичных неоклассических моделях производства значительно упрощены формальные критерии и ограничения деятельности предприятия: не учитываются факторы волатильности товарных и финансовых рынков [7], оказывающие влияние на стоимость компании [4], условия принятия управленческих решений в условиях риска [6, 2, 3] и др. Стоит также отметить, что не полностью учитывается влияние группы налоговых ставок на объем и динамику выпуска предприятия. Этот недостаток преодолен в более поздней работе В.В. Приображенской – А.В. Рыжовой [10], в которой обобщены уже имеющиеся результаты, и в предложенной модели «затраты – выпуск» учтены оттоки по налоговым платежам.
Однако в модели Приображенской – Рыжовой нами обнаружена неточность в формальном описании потока инвестиций, которая исправлена в нижеследующей модели. Приведем ее описание, отметив, что основное ее содержание соответствует оригинальной модели, приведенной в работе [10].
Утверждены детерминированные показатели модели: α – степень однородности производственной функции; с(1) – удельные затраты; θt – доля фонда оплаты труда в оборотных активах.
Обобщены управляемые параметры для интервала планирования t: νt, γt, βt – доли соответственно: инвестиций в оборотные активы (в совокупных инвестициях в производственную сферу), собственных инвестиций в конечном продукте предыдущего планового периода, заемных средств в совокупных инвестициях в производственную сферу.
Кроме того, в модели фигурируют и фиксированные показатели, утвержденные в производственной и финансовой сферах деятельности предприятия:
- ставки τVAT, τUST, τPT, τIT – ставки налогов соответственно: на добавленную стоимость, страховых взносов (единый социальный налог), на имущество и на прибыль;
- процентные ставки
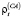 и
и 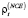 на заемный капитал (по отдельным интервалам с шагом планирования), инвестированный на шаге t соответственно в оборотные и внеоборотные активы;
на заемный капитал (по отдельным интервалам с шагом планирования), инвестированный на шаге t соответственно в оборотные и внеоборотные активы; - μ(t) – норматив амортизационных отчислений для периода t.
Ранее была установлена зависимость в паре «затраты – выпуск» для предприятия с неоклассической производственной функцией степени однородности α, которая задается следующим соотношением [8]:
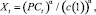 (1)
(1)
где Xt – величина выпуска для периода t; 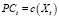 – совокупные затраты на объём выпуска Xt, включенные в рабочий капитал (оборотный капитал производственной сферы).
– совокупные затраты на объём выпуска Xt, включенные в рабочий капитал (оборотный капитал производственной сферы).
Выражение для промежуточного продукта TRt (в стоимостном выражении) получено умножением величины выпуска на цену реализации продукта:
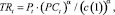 (2)
(2)
где PCt – рабочий капитал, сформированный в начале периода t:
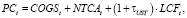 (3)
(3)
где COGSt – амортизация;
τUST – сумма ставок страховых отчислений в Пенсионный фонд;
NTCAt – чистые материальные оборотные активы с учетом НДС:
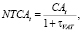
LCFt – фонд оплаты труда.
Поскольку θt – технологически обоснованная доля LCFt в оборотных активах производственной сферы предприятия для периода t, то (3) можно представить в виде
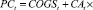
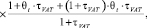 (4)
(4)
где CAt – оборотные активы для периода планирования t.
Освобожденная от налогообложения восстановленная стоимость оборотных активов, являющаяся частью себестоимости, также входит в состав стоимости реализации продукции и фигурирует в инвестиционных потоках в оборотные активы следующего интервала планирования:
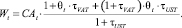 (5)
(5)
Затраты основной производственной деятельности полностью покрываются оборотным капиталом и амортизацией основного капитала:
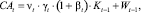 (6)
(6)
где K t – 1 – конечный продукт за период (t – 1).
Тогда рабочий капитал, сформированный в начале пиода t, равен
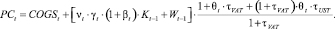
Объем налоговых обязательств выглядит следующим образом:
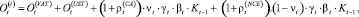
где 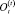 – сумма налоговых отчислений в целом, содержащая составляющие:
– сумма налоговых отчислений в целом, содержащая составляющие:
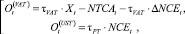 (7), (8)
(7), (8)
налоговые отчисления на добавленную стоимость и в Пенсионный фонд соответственно, где ΔNCEt – изменение стоимости внеоборотного капитала производственной сферы в начале периода (за счет осуществленных инвестиций).
Далее промежуточный продукт TRt очищаем от всех обязательств перед поставщиками, работниками и государством и получаем величину остаточного продукта Yt [8, 11]:
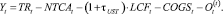 (9)
(9)
В конечном продукте Kt учитывается амортизация, выплаты кредиторам (сумма заемного капитала BCt) и налог на прибыль:
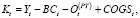 (10)
(10)
где
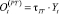 – налоговые отчисления по полученной прибыли. (11)
– налоговые отчисления по полученной прибыли. (11)
Одной из важнейших составляющих денежных потоков предприятия является объем собственных инвестиций:
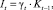 (12)
(12)
где γt – доля собственных инвестиций предприятия в конечном продукте предыдущего планового периода.
Помимо собственных инвестиций ключевое влияние на денежные потоки непосредственно оказывает объем заемных средств в начале шага t:
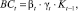 (13)
(13)
где βt – доля заемных средств в совокупных инвестициях в производственную сферу.
Доля (1 – vt) заемного капитала инвестируется во внеоборотные активы:
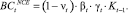 (14)
(14)
Обусловленное инвестициями из всех учитываемых источников изменение внеоборотного капитала на шаге t выглядит следующим образом:
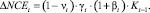 (15)
(15)
C учетом модернизации и амортизации совокупный объем внеоборотного капитала равен:
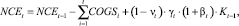 (16)
(16)
где
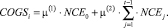 (17)
(17)
Необходимые рекуррентные соотношения представлены ниже:
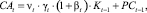 (18)
(18)
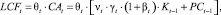 (19)
(19)
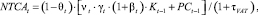 (20)
(20)
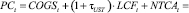
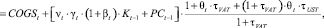 (21)
(21)
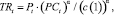 (22)
(22)
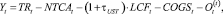 (23)
(23)
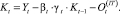 (24)
(24)
Таким образом, инвестиции в производственную сферу следующего периода и полученные дивиденды текущего периода определяют собой величину конечного продукта предприятия:
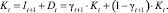 (25)
(25)
На основе полученной модели можно провести комплекс расчетов и оценить влияние экзогенных и эндогенных параметров на динамику «затраты – выпуск». Практические расчеты выполним с исполнением следующих рыночных и технологических констант: τUST = 0,22, τVAT = 0,18, τPT = 0,014, τIT = 0,2 [10], Р = 800, 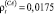 ,
, 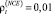 , θ = 0,03, v = 0,9, c(1) = 300. В нулевом периоде внеоборотный капитал NCE0 примем равным 350 000 тыс. руб., оборотные активы CA0 – 25 000 тыс. руб.
, θ = 0,03, v = 0,9, c(1) = 300. В нулевом периоде внеоборотный капитал NCE0 примем равным 350 000 тыс. руб., оборотные активы CA0 – 25 000 тыс. руб.
Расчеты проводились для производственных функций различных степеней однородности (масштаба производства) в интервале (0,75; 0,85), что характеризует соотношение динамики «затраты – выпуск» для реального сектора экономики (предприятия с суммарной эластичностью менее 0,8 относятся к отраслям с низкой добавочной стоимостью, более 0,8 – с умеренной и высокой добавочной стоимостью).
Расчеты показали, что для предприятий обеих групп можно указать величину масштаба производства, являющуюся границей между областями умеренного экспоненциального роста и падения (табл. 1).
Кроме того, на основании полученных расчетов можно сделать вывод, что для выбранного масштаба производства особое влияние на динамику конечного продукта оказывает величина финансового рычага. Для предприятия со степенью однородности α = 0,83 (по нашим данным, наиболее распространенный тип предприятий в обрабатывающих секторах промышленности [11]) результаты расчетов для различных комбинаций управляемых параметров представлены в табл. 6.
Таблица 1
Варианты расчетов экономической динамики предприятия с неоклассической производственной функцией для различных значений параметров α, γt и βt
|
α |
γt |
βt |
Характер динамики «выпуск – затраты» |
|
0,8 |
0,9 |
0,1 |
Умеренное экспоненциальное падение (табл. 2, рис. 1) |
|
0,85 |
0,9 |
0,1 |
Экспоненциальный рост со значительным ростом конечного продукта (табл. 3, рис. 2) |
|
0,8 |
0,5 |
0,5 |
Экспоненциальное падение в начале периода с колебаниями |
|
0,85 |
0,5 |
0,5 |
Умеренный экспоненциальный рост в начале периода с колебаниями |
|
0,75 |
0,5 |
0,9 |
Значительное колебательное падение (табл. 4, рис. 3) |
|
0,85 |
0,5 |
0,9 |
Умеренный экспоненциальный рост со значительными колебаниями в начале периода (табл. 5, рис. 4) |
Таблица 2
α = 0,8; γt = 0,9; βt = 0,1; vt = 0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
28256 |
8358 |
1,04 % |
|
2 |
36178 |
8991 |
0,95 % |
|
3 |
43716 |
7919 |
0,83 % |
|
4 |
49437 |
7474 |
0,70 % |
|
5 |
54003 |
7199 |
0,58 % |
|
6 |
57722 |
6910 |
0,47 % |
|
7 |
60707 |
6654 |
0,38 % |
|
8 |
63087 |
6448 |
0,31 % |
|
9 |
64983 |
6282 |
0,24 % |
|
10 |
66495 |
6149 |
0,19 % |
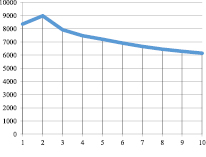
Рис. 1. Kt при α = 0,8; γt = 0,9; βt = 0,1; vt = 0,9
Таблица 3
α = 0,85; γt = 0,9; βt = 0,1; vt = 0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
31137 |
14815 |
3,17 % |
|
2 |
43388 |
18197 |
3,87 % |
|
3 |
56866 |
18952 |
4,27 % |
|
4 |
69126 |
20141 |
4,55 % |
|
5 |
80579 |
21229 |
4,76 % |
|
6 |
91282 |
22043 |
4,89 % |
|
7 |
101139 |
22674 |
4,98 % |
|
8 |
110129 |
23177 |
5,04 % |
|
9 |
118277 |
23579 |
5,08 % |
|
10 |
125624 |
23900 |
5,10 % |
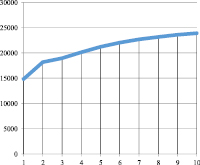
Рис. 2. Kt при α = 0,85; γt = 0,9; βt = 0,1; vt = 0,9
Таблица 4
α = 0,75; γt = 0,5; βt = 0,9; vt = 0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
25706 |
1301 |
– 0,49 % |
|
2 |
28776 |
3768 |
– 0,73 % |
|
3 |
33185 |
2163 |
– 1,07 % |
|
4 |
35922 |
372 |
– 1,29 % |
|
5 |
36969 |
821 |
– 1,40 % |
|
6 |
38130 |
1327 |
– 1,53 % |
|
7 |
39498 |
771 |
– 1,68 % |
|
8 |
40299 |
334 |
– 1,77 % |
|
9 |
40664 |
491 |
– 1,84 % |
|
10 |
41075 |
584 |
– 1,92 % |
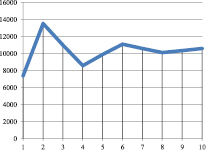
Рис. 3. Kt при α = 0,75; γt = 0,5; βt = 0,9; vt = 0,9
Таблица 5
α = 0,85; γt = 0,5; βt = 0,9; vt = 0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
30708 |
9659 |
3,17 % |
|
2 |
38957 |
17428 |
3,63 % |
|
3 |
51801 |
15159 |
4,20 % |
|
4 |
61492 |
12952 |
4,44 % |
|
5 |
68219 |
14752 |
4,61 % |
|
6 |
75217 |
16487 |
4,81 % |
|
7 |
82523 |
16381 |
4,96 % |
|
8 |
88802 |
16147 |
5,07 % |
|
9 |
94053 |
16616 |
5,16 % |
|
10 |
98913 |
17088 |
5,25 % |
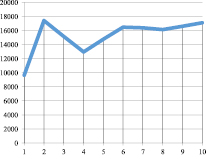
Рис. 4. Kt при α = 0,85; γt = 0,5; βt = 0,9; vt = 0,9
Таблица 6
Варианты расчетов экономической динамики предприятия с масштабом производства 0,83 для различных γt, βt и vt
|
α |
γt |
βt |
vt |
Динамика «выпуск – затраты» |
|
0,83 |
0,9 |
0,9 |
0,1 |
Растущая динамика с большими колебаниями (табл. 7, рис. 5) |
|
0,83 |
0,9 |
0,5 |
0,1 |
Экспоненциальный рост с колебаниями в начале периода |
|
0,83 |
0,9 |
0,1 |
0,5 |
Умеренный экспоненциальный рост (табл. 8, рис. 6) |
|
0,83 |
0,9 |
0,1 |
0,1 |
Умеренный экспоненциальный рост |
|
0,83 |
0,5 |
0,9 |
0,5 |
Растущая динамика с умеренными колебаниями (табл. 9, рис. 7) |
|
0,83 |
0,5 |
0,5 |
0,1 |
Умеренный экспоненциальный рост с колебаниями в начале периода |
|
0,83 |
0,5 |
0,1 |
0,5 |
Умеренный экспоненциальный рост |
|
0,83 |
0,1 |
0,1 |
0,9 |
Экспоненциальный рост (табл. 10, рис. 8) |
|
0,83 |
0,1 |
0,5 |
0,1 |
Умеренный экспоненциальный рост с колебаниями в начале периода |
|
0,83 |
0,5 |
0,9 |
0,9 |
Растущая динамика с затухающими колебаниями |
|
0,83 |
0,1 |
0,9 |
0,1 |
Умеренный экспоненциальный рост с незначительными колебаниями в начале периода |
|
0,83 |
0,1 |
0,5 |
0,9 |
Экспоненциальный рост с незначительными колебаниями |
Таблица 7
α = 0,83; γt = 0,9; βt = 0,9; vt = 0,1
|
t |
PKt |
Kt |
ROEt |
|
1 |
22327 |
4529 |
2,68% |
|
2 |
25962 |
12677 |
1,95% |
|
3 |
30242 |
10493 |
2,41% |
|
4 |
33800 |
6097 |
2,93% |
|
5 |
36607 |
7971 |
2,73% |
|
6 |
39561 |
11106 |
2,47% |
|
7 |
42726 |
10368 |
2,59% |
|
8 |
45596 |
8873 |
2,73% |
|
9 |
48178 |
9735 |
2,63% |
|
10 |
50813 |
11021 |
2,51% |
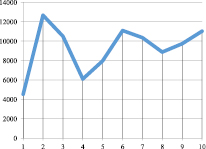
Рис. 5. Kt при α = 0,83; γt = 0,9; βt = 0,9; vt = 0,1
Таблица 8
α = 0,83; γt = 0,9; βt = 0,1; vt = 0,5
|
t |
PKt |
Kt |
ROEt |
|
1 |
25739 |
12086 |
2,27% |
|
2 |
32916 |
13284 |
2,28% |
|
3 |
39780 |
13606 |
2,63% |
|
4 |
45943 |
14082 |
2,71% |
|
5 |
51559 |
14464 |
2,74% |
|
6 |
56674 |
14757 |
2,75% |
|
7 |
61325 |
14991 |
2,75% |
|
8 |
65556 |
15183 |
2,73% |
|
9 |
69411 |
15345 |
2,70% |
|
10 |
72932 |
15486 |
2,68% |
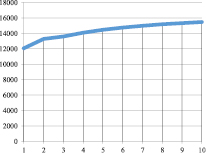
Рис. 6. Kt при α = 0,83; γt = 0,9; βt = 0,1; vt = 0,5
Таблица 9
α = 0,83; γt = 0,5; βt = 0,9; vt = 0,5
|
t |
PKt |
Kt |
ROEt |
|
1 |
25529 |
7558 |
2,27% |
|
2 |
30764 |
13048 |
2,21% |
|
3 |
37529 |
10758 |
2,55% |
|
4 |
42609 |
9050 |
2,71% |
|
5 |
46383 |
10272 |
2,70% |
|
6 |
50168 |
11220 |
2,71% |
|
7 |
53891 |
10977 |
2,76% |
|
8 |
57102 |
10801 |
2,78% |
|
9 |
59888 |
11065 |
2,79% |
|
10 |
62481 |
11284 |
2,79% |
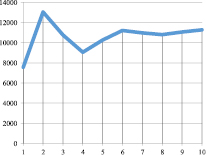
Рис. 7. Kt при α = 0,83; γt = 0,5; βt = 0,9; vt = 0,5
Таблица 10
α = 0,83; γt = 0,1; βt = 0,1; vt = 0,9
|
t |
PKt |
Kt |
ROEt |
|
1 |
21568 |
11638 |
1,88% |
|
2 |
25246 |
12287 |
2,07% |
|
3 |
28499 |
12596 |
2,22% |
|
4 |
31320 |
12912 |
2,34% |
|
5 |
33772 |
13163 |
2,45% |
|
6 |
35900 |
13364 |
2,55% |
|
7 |
37747 |
13527 |
2,64% |
|
8 |
39349 |
13660 |
2,72% |
|
9 |
40738 |
13770 |
2,80% |
|
10 |
41943 |
13863 |
2,88% |
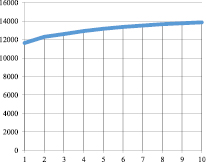
Рис. 8. Kt при α = 0,83; γt = 0,1; βt = 0,1; vt = 0,9
Значимым для экономической теории является следующий результат, полученный на основании расчетов по модели «затраты – выпуск»: наибольшее влияние на величину конечного продукта оказывает ставка налога на добавленную стоимость τVAT, далее (по степени значимости) следуют ставки налога на прибыль τIT и на имущество τPT. Ставка единого социального налога τUST не является определяющим исследуемую динамику фактором. Однако в целом изменения ставок налогообложения не оказывают ключевого влияния на оптимальную структуру рабочего капитала для предприятия, рассматриваемого в табл. 6 масштаба производства.
Таким образом, доминантой динамики «затраты – выпуск» является масштаб производства, соответствующий технологическому уровню производственной системы предприятия. Наиболее важным эндогенным фактором является размер финансового рычага, а среди ставок налогообложения на величину конечного продукта в условиях российской экономики наибольшее влияние оказывает ставка налога на добавленную стоимость.
Библиографическая ссылка
Халиков М.А., Зимина О.С. ОЦЕНКА ВЗАИМНОГО ВЛИЯНИЯ СТАВОК НАЛОГООБЛОЖЕНИЯ И СТРУКТУРЫ КАПИТАЛА КОРПОРАЦИИ НА ФИНАНСОВЫЙ РЕЗУЛЬТАТ В ПРОИЗВОДСТВЕННОЙ СФЕРЕ // Фундаментальные исследования. 2017. № 6. С. 196-203;URL: https://fundamental-research.ru/ru/article/view?id=41573 (дата обращения: 07.02.2026).



