Для стабильного существования любого предприятия необходимо глубокое понимание рыночных процессов, тщательная оценка размеров рынка и его потенциальных возможностей. Для разработки действенной стратегии производства, контроля эффективности ее реализации необходимо оценивать текущий спрос и прогнозировать его изменения [4]. Если компания допустит ошибку при этом, она может упустить огромную прибыль.
Рынок всегда обладает высокой степенью стохастичности, поскольку на него оказывают влияние множество факторов, такие как инфляция, курс валюты, покупательная способность населения и т.д. Непредсказуемость рынка не позволяет сделать точный количественный прогноз спроса на определенный продукт, однако на основании статистических данных есть возможность спрогнозировать благоприятные периоды для реализации производимой продукции. В такие промежутки времени рыночная стоимость продукта превышает его себестоимость и позволяет получить прибыль от продаж. Целью данного исследования является разработка метода прогнозирования таких периодов.
Теория
Прогнозирование объемов сбыта различных типов продукции рассмотрено в работах как отечественных [3, 5, 9, 10], так и зарубежных [13–15] авторов, где используются известные методы экспертных оценок, регрессионного, корреляционного анализа, экстраполяции тренда и т.д. В последнее время в задачах прогнозирования объема сбыта товаров и обоснования маркетинговых решений находит применение теория неопределённости [12], а также метод «нейронных» сетей [1, 11]. Не вдаваясь в детали применения этих методов, отметим, что в каждом конкретном случае выбор метода осуществляется исходя из целей прогнозирования, изменения спроса на изготовляемую продукцию, тенденций изменения платежеспособности предприятий, колебания их деловой активности, цикличности появления на рынке новых товаров конкурентов, изменения технологии производства и т.д. Во всех работах предпринимаются попытки спрогнозировать именно объем сбыта продукции, обобщая его на весь временной промежуток прогнозирования, но, если проанализировать рынок более детально, можно заметить, что тот или иной продукт в разное время воспринимается рынком по-разному [7]. Более того, существуют благоприятные периоды для реализации продукции (предпраздничные дни, дни выдачи заработной платы, сезонность и т.д.), и, безусловно, лица принимающие решения производственного характера, владеют информацией о таких периодах. Однако решения управленцев во многом основаны на интуиции и опыте, поэтому процесс выявления и прогнозирования благоприятных периодов для реализации продукции нуждается в формализации и разработке интуитивно понятных и надежных аппаратов моделирования и прогнозирования.
Несмотря на сложность рыночных процессов в первом приближении, можно считать их марковскими. Это позволяет использовать уравнения Колмогорова для прогнозирования благоприятных периодов реализации продукции. Теория случайных процессов решает для марковского случая три задачи, считающиеся классическими. Применительно к прогнозированию благоприятных периодов для реализации продукции эти задачи формулируются следующим образом.
Средняя величина превышения цены над себестоимостью продукции сводится к взятию интеграла:
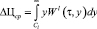
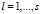, (1)
где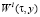 
– условная функция плотности вероятности, τ – время, y – значения цены, Cl – себестоимость данного вида продукции, s – количество видов продукции, учитываемых при расчете. Решение данной задачи проведено в [2] и выражается через функцию параболического цилиндра Dv(z). После ряда преобразований получаем
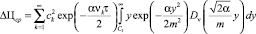, (2)
где vk – корни уравнения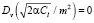 
, α, m2 – параметры модели, а нормирующий множитель вычисляется по формуле
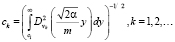(3)
Решение второй задачи позволяет определить среднее время пребывания цены на продукцию в области превышения над себестоимостью и сводится к интегрированию обыкновенного дифференциального уравнения второго порядка относительно среднего времени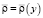 
с соответствующими граничными условиями:
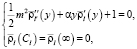
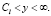(4)
Решая эту краевую задачу, находим
,
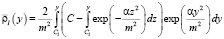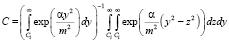. (5)
В третьей задаче получаем оценку среднего числа выбросов значений марковского процесса за данный уровень, которая определяется как решение данного уравнения
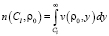. (6)
Решение проводится с помощью преобразования Лапласа при условии, что случайный процесс является стационарным в широком смысле:
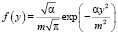. (7)
В отображениях по Лапласу для искомого числа выбросов получаем
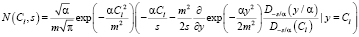. (8)
Обращая найденное выражение, можно найти среднее число выбросов данной продукции за уровень себестоимости.
Высота полученных столбцов показывает лишь превышение цены над себестоимостью в моменты времени, не отражая объемы производства продукции. Однако можно ввести критерий выгодности продукции определив суммарную площадь полученных прямоугольников.
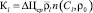. (9)
Данный критерий позволяет определить привлекательность производства того или иного продукта и использовать полученные данные при формировании производственной стратегии [6, 8].
Материалы и методы исследования
Исследование опиралось на статистические данные, предоставленные одним из кондитерских цехов г. Оренбурга. Были проанализированы значения себестоимости и количества произведенной продукции за 2016 г. Исследование проводилось с использованием метода компьютерного моделирования.
Моделировался рынок в виде случайного процесса колебания цены во времени и процесса изменения себестоимости продукции. На основании вышеописанной теории были вычислены значения ΔЦcp,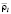 
, 
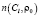и составлена периодическая функция благоприятной реализации продукции. В исследовании был использован шаг расчета в одну неделю с прогнозным периодом равным половине года.
Для компьютерного моделирования в данном исследовании были использованы три модели.
Модель колебания во времени рыночной цены на данный вид продукции является отражением процесса изменения цены на продукт из-за влияния рыночных факторов, таких как покупательная способность населения, активность конкурентов, насыщенность рынка продукцией. В данном исследовании процесс колебания рыночной цены моделировался с помощью генератора случайных чисел с подвижными нижней и верхней границами.
Модель изменения во времени себестоимости изготовления данного вида продукции – это стоимостная оценка используемых в процессе ее производства природных ресурсов, сырья, материалов, энергии, основных фондов, трудовых ресурсов, а также других затрат на производство и реализацию. При более детальном рассмотрении процесса формирования себестоимости добавляются такие факторы, как инфляция, курс валюты, стоимость топлива, тарифы посредников. Эти показатели имеют отчетливо выраженное свойство возрастать во времени, поэтому для более реалистичного представления процесса была использована прогрессивная модель себестоимости.
Модель благоприятных периодов реализации продукции вытекает непосредственно из теории. В исследовании произведена замена моделей колебания рыночной цены и изменения себестоимости на периодическую функцию, отражающую график продаж в виде периодически повторяющихся прямоугольников.
Результаты исследования и их обсуждение
Разработанное программное обеспечение, позволяющее по исходным значениям, заданным пользователем, построить графики изменения во времени себестоимости и рыночной цены. После вычислений, описанных в разделе теории, программа строит периодическую функцию благоприятной реализации продукции, отражающую график продаж в виде периодически повторяющихся прямоугольников.
На рис. 1 представлена экранная форма для ввода исходных данных. Программа позволяет ввести значение себестоимости единицы продукции и выбрать ежемесячный процент изменения себестоимости, а также определить верхнюю и нижнюю границы рыночной себестоимости для моделирования рыночных процессов. С помощью генератора случайных чисел программа формирует набор значений рыночной цены для прогнозного периода.
На рис. 2 представлена экранная форма представления графика изменения во времени себестоимости и рыночной цены на продукцию. Нижней линией представлены значения себестоимости, верхней – представлены значения рыночной цены.
На рис. 3 представлена экранная форма представления периодической функции эффективной реализации продукции, отражающую график продаж в виде периодически повторяющихся прямоугольников.
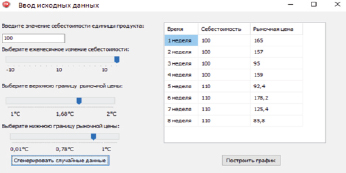
Рис. 1. Экранная форма ввода исходных данных
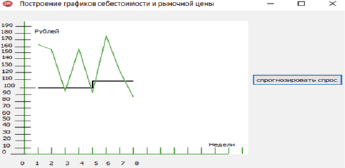
Рис. 2. Экранная форма представления графика изменения во времени себестоимости и рыночной цены на продукцию
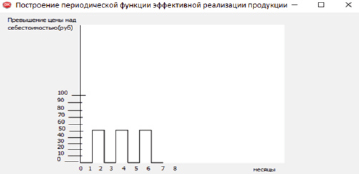
Рис. 3. Экранная форма представления периодической функции благоприятной реализации продукции, отражающей график продаж в виде периодически повторяющихся прямоугольников
Представление процесса прогнозирования в виде такой периодической функции позволяет придать производству ритмичность.
Заключение
Таким образом, метод стохастического прогнозирования периодов благоприятных для реализации продукции представляет модель, отражающую график продаж в виде периодически повторяющихся прямоугольников, и позволяет придать процессу производства ритмичность. На основании теоретического исследования представлен алгоритм прогнозирования, что позволило разработать соответствующее программное обеспечение, имеющее практическую значимость. Поскольку точность прогноза зависит от величины шага и длительности прогнозного периода, необходимы дальнейшие исследования для оптимизации этих параметров.
Библиографическая ссылка
Пищухин А.М., Чернов Ф.В. МЕТОД СТОХАСТИЧЕСКОГО ПРОГНОЗИРОВАНИЯ БЛАГОПРИЯТНЫХ ПЕРИОДОВ РЕАЛИЗАЦИИ ПРОДУКЦИИ // Фундаментальные исследования. – 2017. – № 6. – С. 165-169;URL: https://fundamental-research.ru/ru/article/view?id=41568 (дата обращения: 18.04.2024).