В научной литературе опубликовано немало работ, посвященных изучению динамики зависимости национального дохода от времени в макроэкономических моделях воспроизводства с учетом инвестиционного временного лага между различными величинами, характеризующими процесс воспроизводства (например, накопление в момент времени t зависит от национального дохода и потребления в момент времени t – τ [1–7]. При этом, как известно, национальный доход как функция в зависимости от времени удовлетворяет линейному неоднородному дифференциальному уравнению первого порядка с запаздывающим аргументом.
Настоящая работа посвящена исследованию зависимости национального дохода от времени с учетом инвестиционного временного лага в классической макроэкономической модели Калецкого в случае, когда функция потребления представляет произведение экспоненты и гармонической функции.
Постановка задачи, метод решения и анализ результатов
Рассмотрим экономический цикл воспроизводства в рамках классической экономической модели Калецкого, взяв в качестве основной величины, характеризующей экономический процесс, национальный доход как функцию от времени (Y(t)). Предположим, что существует инвестиционный временной лаг τ между производственным накоплением, приростом национального дохода и потреблением. Тогда основываясь на законе экономического баланса и учитывая инвестиционный временной лаг τ, модель Калецкого можно представить в следующем виде:
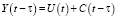, (1)
где Y(t – τ) – национальный доход в момент времени t – τ, C(t – τ) – потребление в момент времени t – τ, U(t) – накопление в момент времени t. Если теперь иметь в виду, что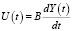 
(B – капиталоемкость национального дохода: отношение производственного накопления к приросту национального дохода) и беря в качестве функции потребления
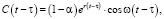(2)
для функции Y(t) из (1) можно получить следующее линейное дифференциальное уравнение первого порядка с запаздывающим аргументом (см. также [2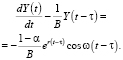, 3])
(3)
Отметим, что в (2) 0 ≤ α ≤ 1 – постоянная норма производственного накопления, ω – частота колебаний функции потребления, r – темп прироста потребления. В работе [1] найдено общее решение уравнения (3) с учетом начального условия Коши
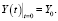(4)
Это решение имеет вид
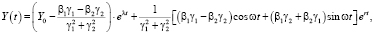(5)
где прирост национального дохода λ с точностью до членов малого параметра λτ в первой степени (решение трансцендентного характеристического уравнения) имеет вид
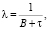(6)
а остальные величины в (5) выражаются формулами
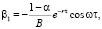
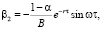(7)
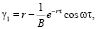
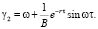(8)
Отметим, что если в (5) перейти к пределу при τ → 0, то получим выражение для Y(t) без учета запаздывания
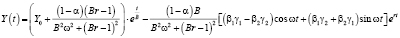. (9)
Полученные результаты (см. формулы (5) и (9)) показывают, что зависимость национального дохода от времени и без учета, и с учетом временного инвестиционного лага имеет осциллирующий характер и с увеличением времени возрастает. Сравнение формул (9) и (5) указывает на то, что учет инвестиционного временного лага в макроэкономической модели воспроизводства Калецкого существенным образом влияет на характер изменения национального дохода в зависимости от времени.
График зависимости прироста национального дохода λ от временного лага τ приведен на рис. 1. Кривые построены согласно формуле (6) для различных значений капиталоемкости национального дохода B(B = 2; 3; 5; 5) при изменении τ от 0 до 14. Они показывают, что прирост национального дохода λ в зависимости от запаздывания τ представляет собой убывающую функцию.
На рис. 2 приведены кривые, выражающие зависимости национального дохода от времени без учета запаздывания τ при постоянном значении капиталоемкости B = 5 и ω = π/2, но при различных значениях темпа прироста потребления r по сравнению с технологическим темпом прироста национального дохода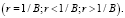 
Кривые построены с помощью формулы (9). Как видно из рис. 2, во всех случаях Y(t) с увеличением t возрастает, сохраняя свой колебательный характер.
Графики зависимости национального дохода от времени (Y(t)) при учете временного лага τ приведены на рис. 3–8. Они построены согласно формуле (5) при постоянных значениях капиталоемкости B (B = 5 и B = 3) и ω (ω = π/2), но при различных значениях темпа прироста потребления r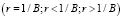 
и времени запаздывания τ. Полученные кривые показывают, что национальный доход в зависимости от времени имеет осциллирующий характер и огибающие максимумов являются возрастающими функциями в зависимости от t. При этом законы возрастания могут быть разными. Например, огибающие максимумов кривых 1 и 2 на рис. 5–8 возрастают приблизительно по экспоненциальному закону, а огибающие кривых 3 и 4 на рис. 3, 5–8 – приблизительно по линейному закону. Следует отметить, что при увеличении временного лага τ скорость возрастания зависимости национального дохода от времени (Y(t)) убывает (см. рис. 3–8).
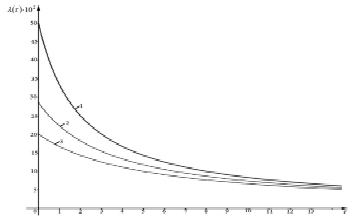
Рис. 1. Зависимость прироста национального дохода λ от временного лага τ при различных значениях B: 1 – B = 2; 2 – B = 3,5; 3 – B = 5
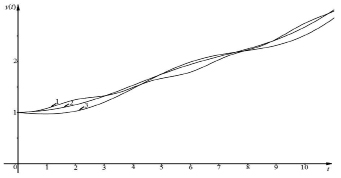
Рис. 2. Зависимость национального дохода Y от времени t в случае отсутствия временного лага: 1 – B = 5, r = 0,2, 2 – B = 5, r = 0,5, 3 – B = 3, r = 0,05
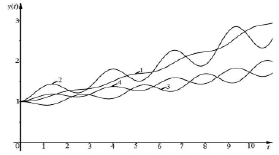
Рис. 3. Зависимость национального дохода Y от времени t при r = 1/B с учетом временного лага: 1 – B = 5, r = 0,2, τ = 0, 2 – B = 5, r = 0,2, τ = 1, 3 – B = 5, r = 0,2, τ = 3, 4 – B = 5, r = 0,2, τ = 5
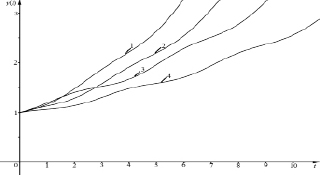
Рис. 4. Зависимость национального дохода Y от времени t при r < 1/B с учетом временного лага: 1 – B = 5, r = 0,05, τ = 0, 2 – B = 5, r = 0,05, τ = 1, 3 – B = 5, r = 0,05, τ = 3, 4 – B = 5, r = 0,05, τ = 5
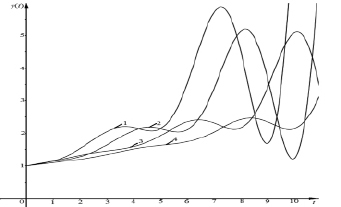
Рис. 5. Зависимость национального дохода Y от времени t при r > 1/B с учетом временного лага: 1 – B = 5, r = 0,5, τ = 0, 2 – B = 5, r = 0,5, τ = 1, 3 – B = 5, r = 0,5, τ = 3, 4 – B = 5, r = 0,5, τ = 5
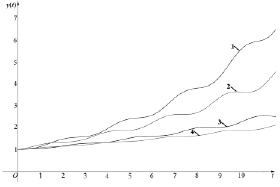
Рис. 6. Зависимость национального дохода Y от времени t при r = 1/B с учетом временного лага: 1 – B = 3, r = 1/3, τ = 0, 2 – B = 3, r = 1/3, τ = 1, 3 – B = 3, r = 1/3, τ = 3, 4 – B = 3, r = 1/3, τ = 5
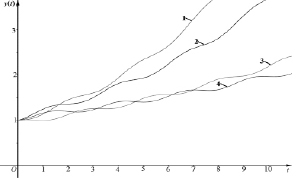
Рис. 7. Зависимость национального дохода Y от времени t при r < 1/B с учетом временного лага: 1 – B = 3, r = 0,03, τ = 0, 2 – B = 3, r = 0,03, τ = 1, 3 – B = 3, r = 0,03, τ = 3, 4 – B = 3, r = 0,03, τ= 5
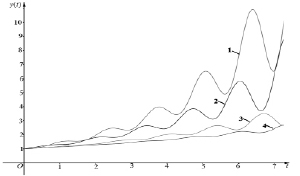
Рис. 8. Зависимость национального дохода Y от времени t при r > 1/B с учетом временного лага: 1 – B = 3, r = 0,6, τ = 0, 2 – B = 3, r = 0,6, τ = 1, 3 – B = 3, r = 0,6, τ = 3, 4 – B = 3, r = 0,6,τ = 5
Заключение
В работе с помощью решения линейного неоднородного дифференциального уравнения с запаздывающим аргументом решена задача динамики изменения национального дохода в зависимости от времени в классической макроэкономической модели Калецкого с учетом инвестиционного временного лага в случае, когда в роли функции потребления выступает произведение экспоненты и периодической функции. Проведенный графический анализ на основе полученных аналитических результатов показывает, что учет временного лага влияет на характер динамики изменения национального дохода в зависимости от времени. Любопытно, что с возрастанием временного лага скорость возрастания национального дохода в зависимости от времени убывает.
Библиографическая ссылка
Геворкян Э.А., Синчуков А.В., Татарников О.В. АНАЛИЗ ДИНАМИКИ ИЗМЕНЕНИЯ НАЦИОНАЛЬНОГО ДОХОДА В МАКРОЭКОНОМИЧЕСКОЙ МОДЕЛИ КАЛЕЦКОГО С УЧЕТОМ ИНВЕСТИЦИОННОГО ВРЕМЕННОГО ЛАГА // Фундаментальные исследования. – 2017. – № 6. – С. 121-126;URL: https://fundamental-research.ru/ru/article/view?id=41560 (дата обращения: 07.12.2024).