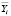Развитие современной техники невозможно без совершенствования производственных технологических процессов. В основе разработки технологических процессов и их оптимизации лежит эксперимент. Результативность экспериментальных исследований значительно вырастает при использовании математических методов анализа. Использование математико-статистических методов при постановке задач разработки технологических процессов, в ходе проведения экспериментов и при обработке полученных данных заметно уменьшает сроки решения, снижает затраты на исследования и повышает качество полученных результатов.
Статистические методы широко применяются при решении задач управления качеством. Роль качества на мировом рынке постоянно возрастает. Стремление вписаться в этот рынок вынуждает современные предприятия становиться участниками гонки за качеством. Все новации в области обеспечения качества становятся очень востребованными. Новые методики в области планирования эксперимента позволяют получать математические модели устойчивости технологических процессов.
Сравнение различных подходов для решения инженерных задач в технологии машиностроения позволит выработать рекомендации по выбору наиболее эффективного метода для каждого случая.
Материалы и методы исследования
Оценка эффективности статистических методов осуществлялась по результатам экспериментов токарной обработки, как одной из самых распространенных в машиностроительном производстве.
В качестве объекта исследования был выбран пруток диаметром 55 мм, марки ЛС59-1. Латуни отличаются сравнительно высокими механическими свойствами, являются коррозионно-устойчивыми и имеют низкую стоимость, что позволяет широко применять их в сфере машиностроения.
Был проведён полный факторный эксперимент, в котором факторы установлены на двух уровнях. Методика проведения такого эксперимента подробно рассмотрена в работах [1–4; 6–10]. В качестве независимых факторов выбрана частота вращения шпинделя и продольная подача. Обработка осуществлялась на токарно-винторезном станке модели ИЖ-250ИТП.
В планах многофакторных экспериментов и при обработке результатов эксперимента с целью получения математической модели вводится понятие уровней факторов, нулевого (или основного) уровня, а также интервала варьирования факторов. Такое представление необходимо для того, чтобы все факторы в эксперименте представить в безразмерном нормализованном масштабе. При переходе от натурального масштаба уровней факторов к нормализованному наибольшее значение уровня обозначается как (+1) – верхний уровень, и нижний уровень – меньшее значение уровня фактора (–1), основной обозначают (0).
В частности, подачу s изменяли от 0,075 мм/об X1(–1) до 0,15 мм/об X1(+1), частоту вращения шпинделя n – от 500 1/мин X2(–1) до 1000 1/мин X2(+1).
При переходе от натуральных значений уровней факторов к нормализованным был рассчитан основной уровень:

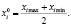
Наряду с понятиями верхнего и нижнего уровней факторов, а также нулевого уровня вводится понятие интервала варьирования факторов, который представляет собой половину разности верхнего и нижнего уровней факторов:

Зная нулевой уровень и интервал варьирования переходят от натурального масштаба к нормализованному по формуле
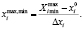
Уровни факторов и интервалы их варьирования в натуральном и нормализованном масштабах приводятся в табл. 1.
В качестве отклика (Y) фиксировалась шероховатость обработанной поверхности (Ra). Измерение шероховатости поверхностей выполнялось на профилометре-профилографе модели АБРИС – ПМ7.
Все опыты в эксперименте повторялись по 3 раза и их последовательность рандомизирована.
Результаты исследования и их обсуждение
На первом этапе исследования выполнен регрессионный анализ результатов полного факторного эксперимента. Для каждой строки матрицы с учетом повторных опытов определили среднее значение отклика, дисперсию для каждого опыта и сумму выборочных дисперсий. Полученные данные представлены в табл. 2.
Обработка результатов эксперимента:
1. Для каждой строки матрицы с учетом повторных опытов (n = 3) было определено среднее значение отклика:
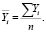
2. Выборочная дисперсия для каждого опыта:
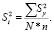
3. Для проверки гипотезы об однородности ряда дисперсий по G-критерию было определено его расчётное значение:
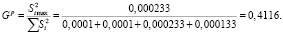
Таблица 1
Уровни факторов и интервалы их варьирования в натуральном и нормализованном масштабах
|
Факторы |
Уровни факторов |
Интервал варьирования, Δxi |
||
|
+1 |
0 |
–1 |
||
|
X1(s, мм/об) |
0,15 |
0,1125 |
0,075 |
0,0375 |
|
X2(n, 1/мин) |
1000 |
750 |
500 |
250 |
Таблица 2
Результаты эксперимента
|
№ п/п |
s |
n |
Параллельные опыты, Ra мкм |
|
|
||
|
Y1 |
Y2 |
Y3 |
|||||
|
1 |
0,15 |
1000 |
1,67 |
1,68 |
1,66 |
1,670 |
0,000100 |
|
2 |
0,075 |
1000 |
1,43 |
1,42 |
1,44 |
1,430 |
0,000100 |
|
3 |
0,15 |
500 |
1,78 |
1,77 |
1,75 |
1,767 |
0,000233 |
|
4 |
0,075 |
500 |
2,04 |
2,04 |
2,06 |
2,047 |
0,000133 |
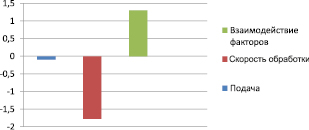
Рис. 1. Графическое представление влияния факторов на отклик
Табличное значение: 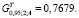
Так как Gp < GT, то выдвинутая гипотеза об однородности дисперсий с доверительной вероятностью 95 % была принята.
4. Так как дисперсии однородны, была вычислена дисперсия воспроизводимости:

5. Были рассчитаны коэффициенты уравнения регрессии.
6. Проверка гипотезы о статической значимости коэффициентов уравнения регрессионного анализа:
а) дисперсия коэффициентов регрессии и соответствующее стандартное отклонение:
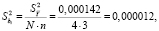
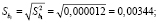
б) доверительный интервал для всех коэффициентов регрессии:
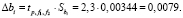
Так как коэффициенты регрессии по абсолютной величине больше величины доверительного интервала, то ни один из них не был отброшен и гипотеза о статической значимости коэффициентов регрессии с доверительной вероятностью 95 % принята.
В этом случае уравнение регрессионного анализа в нормализованном масштабе уровней факторов имеет вид
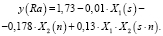
Выводы
1. Наиболее сильное влияние на отклик (шероховатость обработанной поверхности) оказывает частота вращения шпинделя (n). Влияние этого фактора в 1,4 раза сильнее эффекта взаимодействия факторов n и s, а также почти в 18 раз сильнее влияния подачи.
2. Увеличивая частоту (n) с 500 до 1000 1/мин, уменьшаем шероховатость. Увеличивая подачу от 0,075 до 0,15, шероховатость также уменьшаем.
Сильное влияние эффекта взаимодействия объясняется тем, что влияние подачи возрастает с увеличением скорости обработки.
Для применения уравнения регрессионного анализа в практических целях его необходимо представить в натуральном масштабе уровней факторов. Нормализованные значения уровней факторов связаны с натуральными следующими зависимостями:

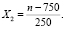
Уравнение регрессионного анализа в натуральном масштабе имеет вид
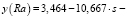
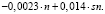
Дополнительно был проведен дисперсионный анализ. Дисперсионный анализ позволяет, при исследовании технологических систем, определить вклад каждого фактора в дисперсию отклика. Сущность его заключается в разложении суммы квадратов отклонений выходного параметра системы от общего среднего на компоненты, соответствующие предполагаемым источникам изменчивости выходного значения. Наиболее результативен дисперсионный анализ в экспериментах с одновременным изучением двух и более факторов [11, с. 25].
Дисперсионный анализ показал, что фактором частоты вращения шпинделя обусловлено 65,04 % дисперсии отклика (Ra), и лишь 0,205 % – подачей. Вклад совместного влияния двух факторов в дисперсию отклика 34,562 %.
В настоящее время для статистического контроля и оценки качества изделий широко применяются методы Тагути, основанные на многофакторных экспериментах. В основе концепции Тагути лежит поиск таких технологических режимов, при которых отклик – оцениваемый параметр качества – меньше всего изменяется под воздействием неконтролируемых факторов, так называемых шумов. Такую устойчивость и способность демпфировать шумы называют робастностью. В соответствии с методами Тагути, при обработке многофакторного эксперимента наряду с обычными отклонениями отклика в каждом опыте измеряется также показатель, определяемый отношением сигнал/шум и представляющий собой меру разброса отклика для контролируемых факторов при варьировании неконтролируемых [4; 5; 8; 12].
Тагути определил три типа отношений сигнал/шум (с/ш), определяемых тем обстоятельством, какое заданное значение отклика является наилучшим: как можно меньшее, как можно большее или некоторое конечное [12].
Если требуется обеспечить наименьшую шероховатость, то применяют для расчета соотношений с/ш зависимость, которую Тагути назвал «как можно меньше»:
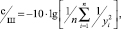
где n – число повторных опытов в каждой строке плана ПФЭ; yi – значение отклика в каждом повторном опыте строки плана.
Результаты расчетов по формуле (с/ш) представлены в табл. 3.
Таблица 3
Результаты анализа методом «сигнал/шум»
|
№ п/п |
s |
n |
Параллельные опыты, Ra, мкм |
С/Ш |
||
|
Y1 |
Y2 |
Y3 |
||||
|
1 |
0,15 |
1000 |
1,67 |
1,68 |
1,66 |
4,454 |
|
2 |
0,075 |
1000 |
1,43 |
1,42 |
1,44 |
3,106 |
|
3 |
0,15 |
500 |
1,78 |
1,77 |
1,75 |
4,942 |
|
4 |
0,075 |
500 |
2,04 |
2,04 |
2,06 |
6,221 |
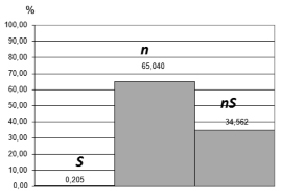
Рис. 2. Результаты ПФЭ по методике дисперсионного анализа
Сравнивая опытные данные для уровней фактора n (на верхнем уровне) и при различных s, можно сделать вывод, что наибольшая робастность, т.е. устойчивость оцениваемого параметра Ra, обеспечивается, когда подача соответствует верхнему уровню. Однако на нижнем уровне n наибольшая робастность достигается на нижнем уровне s.
Получено уравнение с/ш, которое показывает вклад в устойчивость процесса. Из уравнения видно, что наибольший вклад в устойчивость процесса при наружном продольном точении вносит эффект парного взаимодействия.
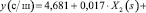
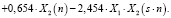
Заключение
В ходе выполнения работы была проведена обработка эксперимента точения латуни и построены математические модели. Полученные математические модели подвергались дисперсионному анализу, регрессионному анализу и анализу методом Тагути с/ш. Регрессионный анализ показывает силу влияния каждого фактора, а также характер его изменения, однако требует подготовки исследователя и занимает много времени. Дисперсионный анализ показывает силу влияния каждого фактора и его вклад в общую дисперсию, но не устанавливает характер их влияния. При этом он очень сложен в вычислении, что требует привлечения дорогостоящей техники и программного обеспечения. Его рекомендуют проводить только совместно с регрессионным анализом. Метод с/ш в свою очередь не требует специальных программ и может проводиться в случаях, когда существуют ограничения во времени, а также показывает при какой комбинации уровней факторов отклик обладает наибольшей устойчивостью (робастностью), но к его недостаткам можно отнести то, что он не определяет характер влияния факторов на отклик.
Библиографическая ссылка
Калмыков В.В., Федорова О.С., Малышев И.Е. ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ АНАЛИЗА ТЕХНОЛОГИЧЕСКИХ ФАКТОРОВ ПРИ ТОКАРНОЙ ОБРАБОТКЕ // Фундаментальные исследования. 2017. № 6. С. 48-52;URL: https://fundamental-research.ru/ru/article/view?id=41546 (дата обращения: 07.02.2026).
DOI: https://doi.org/10.17513/fr.41546