Существуют такие области человеческой жизнедеятельности, в которых низкий уровень надёжности программного обеспечения (ПО) предопределяет высокую вероятность отказа, результатом которого может стать урон здоровью и жизни людей, а также значительные финансовые издержки. К таким областям относятся: атомная энергетика, химическая, металлургическая, военная и космическая отрасли промышленности и т.п.
Одним из наиболее хорошо себя зарекомендовавших подходов к повышению надёжности программного обеспечения является методология мультиверсионного программирования [2].
Для обеспечения высокого уровня надёжности версии модулей должны быть диверсифицированы. Диверсификация ПО осуществляется на четырёх уровнях:
1. Уровень алгоритмов.
2. Уровень языков программирования.
3. Уровень средств разработки.
4. Уровень средств тестирования [13].
Для обеспечения диверсификации различных версий модулей мультиверсионного ПО (МВПО) их разработка выполняется независимыми друг от друга группами разработчиков [3]. Однако в [3] также указывается, что такой подход отличается высокой стоимостью. При этом считается, что при такой независимой разработке версии модулей являются диверсифицированными по умолчанию. Однако на практике это оказывается не всегда так.
Для определения степени диверсифицированности версий модулей МВПО на уровне алгоритмов авторами предлагается введение метрики, определяющей степень различия между версиями.
Исследовательская гипотеза
Поскольку версии модулей МВПО выполняют какие-либо вычислительные операции над данными, авторами данной работы была выдвинута гипотеза, что определение меры различия версий на уровне алгоритмов может осуществляться путём сравнения изменений данных, обрабатываемых модулем.
Проверка данной гипотезы была осуществлена на примере алгоритмов внутренней сортировки числовых массивов.
Зачастую поведение вычислительных математических алгоритмов не инвариантно, т.е. один и тот же алгоритм может вести себя по-разному при подаче ему на вход различных данных. В связи с этим для обеспечения чистоты эксперимента необходимо осуществить систематический обход различных путей выполнения каждой сравниваемой программной реализации алгоритма.
Для удовлетворения данного требования был применён тот же подход, что используется при автоматизированной генерации unit-тестов. Несмотря на то, что мультиверсионное ПО как объект для применения подхода автоматизированной генерации тестов является новой областью, за счет его использования становится возможным прохождение всех ветвей кода каждого алгоритма.
Построение дерева выполнения программного алгоритма
С некоторыми допущениями на базовом уровне выполнение программы состоит из последовательных вызовов инструкций присваивания, а также условных и безусловных переходов [11]. В совокупности различные варианты выполнения программы образуют дерево выполнения. Корень дерева выполнения представляет собой точку входа, каждый из листов – точку выхода программы или подпрограммы. Маршрут вдоль ветвей дерева выполнения задается теми входными данными, которые подаются на вход программе. Таким образом, для исследования различных вариантов работы программы необходимо иметь различные входные данные, для чего может быть построен генератор входных данных.
Стоит отметить, что для многих программ дерево выполнения может иметь бесконечный размер, также некоторые пути могут не рассматриваться из-за технических ограничений генератора входных данных. Таким образом, для определения полноты тестового набора вводится критерий покрытия кода [7]. В данном случае тестовый набор считается адекватным, если он покрывает все ветви в графе потока [6] целевой программы.
Одной из методик, применяемых для систематической генерации входных тестовых данных, являются динамические символьные вычисления [8–12]. При использовании динамических символьных вычислений программы части входных данных рассматриваются как символьные неограниченные входы, другие же рассматриваются как конкретные. Во время выполнения программы накапливаются ограничения над символьными входами, которые в дальнейшем применяются для исследования альтернативных путей.
Авторами был реализован инструмент, позволяющий отслеживать изменения значений, хранимых в памяти программы. В рамках проведённого исследования отслеживались изменения значений, входящих в состав массивов, подаваемых на вход алгоритмам сортировки. Изменения отслеживались при входе в каждый новый базовый блок и при выходе из подпрограммы [14]. При дальнейшем изложении под шагом работы алгоритма будем понимать прохождение базового блока, сопровождаемое выводом промежуточных результатов сортировки. Под трассой будем понимать совокупность изменений входных данных, произведенных за время работы алгоритма, это отличается от классического понимания трассы [12].
Методы анализа результатов эксперимента
С целью выполнения анализа, а также введения меры различия между алгоритмами (метрики) для предметной области алгоритмов сортировки было определено следующее:
1. Массив на каждом шаге его сортировки – точка в многомерном пространстве.
2. Каждые две точки в многомерном пространстве образуют вектор.
3. Совокупность изменений значений входного массива за время работы алгоритма образует трассу.
4. Если в течение нескольких шагов алгоритма значение сортируемого массива остаётся неизменным, точка остаётся на месте.
Таким образом, определение метрики различия между алгоритмами может быть осуществлено по нескольким признакам:
1) отношение длины сортируемого массива (мерности пространства точки) к количеству шагов, т.е. условная скорость прохождения трассы:
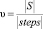 ,
,
где |S| – мерность пространства точки, |steps| – количество точек в трассе;
2) количество и продолжительность общих отрезков у двух трасс, определим степень схожести алгоритмов (D) как
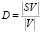 ,
,
где |V| – количество рёбер трассы 1, |SV| – количество рёбер трассы 1, совпадающих с рёбрами трассы 2;
3) длина (продолжительность) трасс:
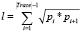 ,
,
где l – длина всей трассы, |Trace| – количество точек в трассе, pi – текущая точка трассы, pi – следующая после текущей точка трассы;
4) отношение длины прямого пути от начальной до конечной точки и длины всей трассы:
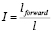 ,
,
где lforward – длина прямого пути от первой до последней точки трассы, l – длина трассы.
Важно отметить, что такой подход позволяет определить наличие клонов среди алгоритмов, а также алгоритмы, эквивалентные друг другу.
Под клоном обычно подразумевается какой-либо исходный код, который применяется без изменений в нескольких различных программах [1]. Так как в данной работе обсуждается диверсификация ПО на уровне алгоритмов, то понятие «клон» имеет иное значение.
Авторами принято считать клонами две программные реализации алгоритмов, трассы выполнения которых полностью совпадают, то есть если выполняются следующие условия:
1. 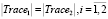 ,
,
где |Trace| – количество точек в трассе
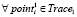 и
и 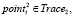
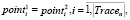
где Tracen – сравниваемая трасса, 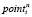 – текущая точка в n-й трассе,
– текущая точка в n-й трассе, 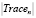 – количество точек в n-й трассе,
– количество точек в n-й трассе, 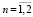 , в случае, если условие 1 выполнено.
, в случае, если условие 1 выполнено.
В данном контексте программные реализации алгоритмов считаются эквивалентными, если при подаче им на вход идентичных наборов данных они выдают идентичные результаты. Учитывать, являются ли две программные реализации алгоритмов клонами, имеет смысл только в случае их эквивалентности.
Особенности реализации
В данной работе использован генератор тестов [5], построенный по архитектуре EXE [8]. Для работы с генератором пользователю необходимо написать драйвер на языке Си. Генератор порождает тесты также на языке Си, которые далее компилируются и запускаются.
Для получения трасс разработана отдельная утилита для трансформации LLVM-IR кода [14]. Данным средством инструментируются операции выделения памяти в стеке, входные точки базовых блоков, а также точки выхода из функций. При распределении памяти в стеке утилита сохраняет указатель на хранимое значение и затем выводит его в нужном формате при входе в каждый базовый блок и выходе из функции, обеспечивая создание трасс в требуемом виде.
Результаты эксперимента
Для проведения эксперимента были написаны функции на языке C (Си), реализующие 3 алгоритма сортировки: пузырьковая сортировка, быстрая сортировка, простой выбор [4].
Для каждого алгоритма при помощи динамических символьных вычислений был порожден набор тестовых данных. Таким образом, было получено 3 тестовых набора для каждого из трех алгоритмов. В общей сложности было сгенерировано 104 тестовых случая: 24 – для пузырьковой сортировки, 47 – для быстрой сортировки и 33 – для простого выбора. При этом полученное покрытие кода соответствует как критерию покрытия инструкций, так и покрытия переходов. Размер символьного массива, подаваемого на вход, был ограничен четырьмя элементами.
Каждый алгоритм был запущен на трех тестовых наборах, таким образом, в результате было сгенерировано 9 наборов трасс для трех различных реализаций, т.е. в ходе эксперимента было получено и проанализировано 312 трасс. Это необходимо для оценки различий между ними [15]. Следует отметить, что каждому тестовому случаю в тестовом наборе соответствует определенная трасса. Полученные трассы были проанализированы с последующим вычислением метрик.
Результаты работы теста алгоритма простой выбор
|
Итерация |
Метод пузырька |
Быстрая сортировка |
Простой выбор |
|||
|
№ |
Координаты точки |
Расстояние до конечной точки |
Координаты точки |
Расстояние до конечной точки |
Координаты точки |
Расстояние до конечной точки |
|
1 |
{–1, –2, –7, –8} |
4,23 |
{–1, –2, –7, –8} |
4,23 |
{–1, –2, –7, –8} |
4,23 |
|
2 |
{–2, –1, –7, –8} |
4,15 |
{–8, –2, –7, –1} |
1,22 |
{–8, –2, –7, –1} |
1,22 |
|
3 |
{–2 ,–7, –1, –8} |
2,20 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
|
4 |
{–2, –7, –8, –1} |
1,81 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
|
5 |
{–7, –2, –8, –1} |
1,54 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
|
6 |
{–7, –8, –2, –1} |
0,05 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
|
7 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
{–8, –7, –2, –1} |
0,00 |
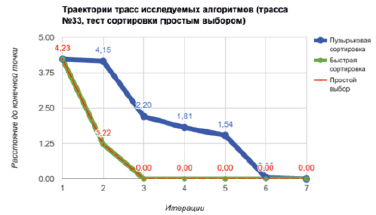
Траектории трасс исследуемых алгоритмов
Поскольку представление результатов анализа всех 312 трасс является слишком объёмным и, как следствие, неприемлемым для приведения в данной статье, авторами было принято решение в качестве результатов эксперимента привести трассы для одного тестового случая.
Значения полученных трасс и расстояния каждой текущей точки до конечной представлены в таблице. На рисунке показаны траектории трасс для каждого из алгоритмов. Красным цветом (пунктиром) выделен график алгоритма, соответствующий запускаемому тесту.
На рисунке ось абсцисс соответствует количеству итераций. По оси ординат отмечаются расстояния от текущей до конечной точки работы алгоритма, которые определяются по формуле
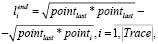
где |Trace| – длина трассы, pointlast – конечная точка трассы, pointi – текущая точка трассы.
Проанализируем результаты, полученные на основании запуска теста, сгенерированного для сортировки методом простого выбора.
1. Условная скорость прохождения трасс:
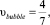
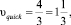
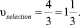
2. Общие отрезки с другими трассами.
Трасса алгоритма пузырьковой сортировки не имеет общих отрезков с другими трассами, т.е. совпадает с ними на 0 %.
Трассы алгоритмов быстрой сортировки и простого выбора совпадают друг с другом на 100 %.
3. Длины трасс:
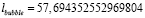 ,
,
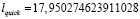 ,
,
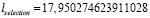 .
.
4. Показатели близости длины трасс к длине прямого пути:
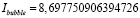 ,
,
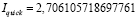 ,
,
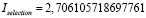 ,
,
при 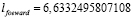 .
.
При анализе трасс всех тестовых случаев, включая приведенный выше, было выявлено, что:
1. Все алгоритмы эквивалентны, т.е. при подаче на вход одинаковых данных они выдают одинаковый результат.
2. Алгоритм пузырьковой сортировки значительно отличается от остальных алгоритмов, как по протяженности трассы и всех величин, вытекающих из неё, так и по количеству общих точек и отрезков.
3. Алгоритмы быстрой сортировки и простого выбора являются клонами, значения всех их показателей диверсифицированности совпадают.
Заключение
Таким образом, введение метрики различия ПО на уровне алгоритмов позволяет автоматически определять количественную степень различия на уровне алгоритмов между различными версиями модулей МВПО. При этом наличие спецификации не требуется – необходим только исходный код.
Кроме того, использование такой метрики может быть полезно, как на этапе разработки мультиверсионного программного обеспечения для оперативного внесения корректировок в разрабатываемый код, так и на этапе использования МВПО в готовом программном комплексе, например в процессе голосования, определяющего корректность результатов работы модулей.
Библиографическая ссылка
Грузенкин Д.В., Якимов И.А., Кузнецов А.С., Царев Р.Ю. ОПРЕДЕЛЕНИЕ МЕТРИКИ ДИВЕРСИФИЦИРОВАННОСТИ МУЛЬТИВЕРСИОННОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ НА УРОВНЕ АЛГОРИТМОВ // Фундаментальные исследования. 2017. № 6. С. 36-40;URL: https://fundamental-research.ru/ru/article/view?id=41544 (дата обращения: 07.01.2026).



