В настоящее время в связи с быстрым развитием микропроцессорной техники основное внимание уделяется проектированию электронной части системы автоматического управления силовой установки (САУ СУ).
Существующие на данный момент методы расчета гидромеханической САУ СУ довольно неудобны для анализа систем управления, и требуют значительных вычислительных затрат. В частности, метод линеаризации нелинейных уравнений системы, хотя и позволяет найти статические значения параметров агрегата дозирования топлива (АДТ) системы управления, но требует применения разложения в ряд Маклорена, что приводит к значительным вычислительным затратам, и трудно поддается формализации, что чрезвычайно важно при реализации расчетов на компьютере [1].
Поэтому значительный интерес представляет сетевой метод расчета АДТ, позволяющий производить расчеты посредством матричных операций, которые относительно легко формализуются и довольно просты в машинной реализации.
Целью работы является разработка методики расчета статического режима работы гидромеханической АДТ с точки зрения максимальной формализации метода для последующей реализации на компьютере. Реализация данного метода позволит значительно сократить время расчета, увеличить производительность труда инженера-конструктора [2].
Постановка задачи
Рассмотрим схему АДТ одного из поколений, которое относится к классу двумерных САУ (рис. 1).
Величина расхода топлива зависит от величины переменного сечения окна дозирующей иглы (fиглы), величина которого в свою очередь определяется положением сервопоршня (на схеме не показан). При этом на переменном сечении окна fиглы поддерживается заданный перепад давлений P1 – P2 = const с помощью двух клапанов постоянного перепада. Питание осуществляется от топливно-нагнетающего агрегата (Pн = const).
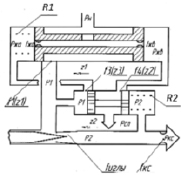
Рис. 1. Схема АДТ (R1, R2 – величины затяжки пружины; z1, z2 – координаты подвижных элементов; fиглы – величина переменного сечения окна дозирующей иглы; f1(z1), f3(z3), f4(z2) – площади сечения трубопровода (или жиклера); Pн – давление от качающего узла; P1 и P2 – давление в клапане перепада в левой и правой полостях; Pсл – давление слива; Pкс – давление камеры сгорания; fкс – площадь форсунок камеры сгорания; Pжа – давление в левой полости; Pжв – давление в правой полости; fжа, fжв – площади жиклеров в левой и правой полостях)
Рассмотрим, как будут меняться величины внутренних потоков Q и координаты подвижных элементов z1, z2 при изменении затяжки пружины R2. Для исследования этого процесса воспользуемся методикой моделирования дозирующего устройства сетевыми моделями.
Методы решения
Для моделирования АДТ с помощью сетевых моделей необходимо построить граф сети. На схеме АДТ места соединений потоков жидкости перенесем на граф сети в виде узла. Для каждого узла указывается давление Pi. Трубопроводы, которыми соединены узлы, обозначаются дугами и указываются для них веса, которые равны значению d(f):
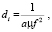 (1)
(1)
где f – площадь сечения трубопровода/жиклера, µ – коэффициент истечения.
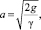 (2)
(2)
где 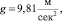 γ – удельный вес топлива.
γ – удельный вес топлива.
На граф (рис. 2) наносятся внешние потоки: Qн – поток, поступающий в АДТ, Qслива – поток слива топлива (возврат в топливный бак), Qкс – поток топлива, поступающий в камеру сгорания.
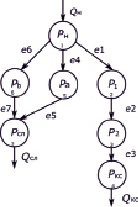
Рис. 2. Граф сети АДТ для расчета статических характеристик
Анализ статического режима гидромеханической системы сетевыми моделями
По условиям работоспособности АДТ в статическом равновесии (z1 = 0, z2 = 0) необходимо, чтоб разность давлений соответствовала заданной величине P1 – P2 = 7,5 кг/см2 [1].
Первая подсистема уравнений – это система дифференциальных уравнений, отражающая закон изменения координаты положения подвижных элементов (ПЭ) АДТ во времени:
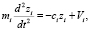 (3)
(3)
где 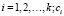 ; – эквивалентная жесткость пружины i-го ПЭ; mi – масса i-го ПЭ;
; – эквивалентная жесткость пружины i-го ПЭ; mi – масса i-го ПЭ; 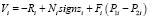 – возмущающая сила, воздействующая на i-й ПЭ; Ri – величина начального усилия на i-м ПЭ; Ni – сила трения покоя i-го ПЭ; Fi – площадь поперечного сечения поршня i-го ПЭ; P1i и P2i – давления в полостях, ограничивающих перемещение i-го ПЭ.
– возмущающая сила, воздействующая на i-й ПЭ; Ri – величина начального усилия на i-м ПЭ; Ni – сила трения покоя i-го ПЭ; Fi – площадь поперечного сечения поршня i-го ПЭ; P1i и P2i – давления в полостях, ограничивающих перемещение i-го ПЭ.
Из условий эксплуатации известны давления в узлах 1, 4, 7, а также конструкторские параметры, приведённые в табл. 1.
Таблица 1
Конструкторские параметры
|
Исходные данные для расчетов |
||||||||
|
m1 |
0,18 |
кг |
Pн |
6 865 000 |
Па |
Qн |
30000 |
л/час |
|
F1 |
0,014 |
м |
Pкс |
392 300 |
Па |
Qкс |
4000 |
л/час |
|
с1 |
0,9022118 |
Н/м |
Pслива |
303 975 |
Па |
Qслива |
26000 |
л/час |
|
dжа |
0,008 |
м |
f2 |
78,155 |
мм2 |
P1 – P2 |
735498,75 |
Па |
|
dже |
0,008 |
м |
fи |
10 |
мм2 |
µ |
0,7 |
|
|
m2 |
0,03 |
fкс |
2,11 |
мм2 |
a |
819 |
||
|
F2 |
1,22 |
м |
с2 |
1,02969825 |
Н/м |
h3, h4 |
2 |
|
Для того, чтобы составить математическую модель АДТ, необходимо описать по известным формулам [3, 4] подсистему уравнений равновесия ПЭ; подсистему уравнений, обеспечивающих выполнение закона сохранения потоков в узлах (выписывается для всех узлов графа); подсистему уравнений, определяющих падение давления на различных участках сети в зависимости от величины потока.
Топология сети может быть описана с помощью матрицы соединений, или инциденций Ai [3]. Матрица соединений – прямоугольная, число ее строк равно числу узлов, а число столбцов равно числу ветвей сети.
Для графа (рис. 2) составим матрицу соединений (инциденций) и контурную матрицу данного графа.
Матрица соединений (инциденций):
 .
.
Контурная матрица:
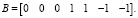
Требуется получить значения вектора внешних потоков системы Qs. Вектор Qs представляет собой внешние по отношению к системе потоки, втекающие в каждый ее узел. Знание величин этих потоков необходимо для проектирования силовой установки летательного аппарата. Его размерность равна количеству узлов графа АДТ. Если в узел не втекает внешний поток, то его величина принимается за ноль. Втекающие потоки записываются положительными значениями, а выходящие – отрицательными, при этом необходимо соблюдать баланс между ними. Для данной схемы вектора внешних потоков (значения даны в литрах в час) следующие:
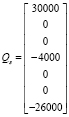 .
.
Первому элементу вектора соответствует первый узел графа АДТ, второму – второй и т.д.
Методику расчета подсистем уравнений можно описать следующими этапами:
1. Задается величина затяжки пружины R2 с учетом силы трения (как правило, известна из прототипа).
2. Определяется координата положения подвижного элемента:
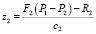 .
.
3. Величины d3, d4 определяются по формуле (1), где площадь сечения отверстий 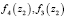 определяются по формуле
определяются по формуле
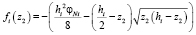 ,
,
где 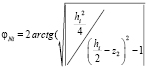 – изменение угла при перемещении между fi и zi поршня, т.е. степень открытия или закрытия отверстия; hi – разница между zi и ri, гдe ri – радиус отверстия.
– изменение угла при перемещении между fi и zi поршня, т.е. степень открытия или закрытия отверстия; hi – разница между zi и ri, гдe ri – радиус отверстия.
4. Величины внутренних потоков и величины давлений вычисляются по формулам
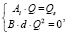
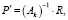
где
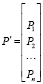 ,
,
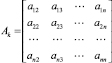 ,
,
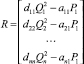 ,
,
при условии, что P1 – P2 = const.
Таблица 2
Результаты расчета при заданной величине R2
|
R2 (задано) |
R1 |
z1 |
z2 |
Pb |
Q1 |
Q2 |
Q3 |
Q4 |
Q5 |
Q6 |
Q7 |
|
кг |
кг |
мм |
Мм |
Па |
л/час |
л/час |
л/час |
л/час |
л/час |
л/час |
л/час |
|
2,60 |
5,640301 |
5,9948 |
6,3611 |
303975 |
4000 |
4000 |
4000 |
25944,499 |
25944,499 |
55,501 |
55,501 |
|
2,80 |
5,237850 |
5,5601 |
6,1669 |
303975 |
4000 |
4000 |
4000 |
25940,947 |
25940,947 |
59,053 |
59,053 |
|
3,00 |
4,855251 |
5,1467 |
5,9726 |
303975 |
4000 |
4000 |
4000 |
25936,963 |
25936,963 |
63,037 |
63,037 |
|
3,05 |
4,762583 |
5,0466 |
5,9241 |
303975 |
4000 |
4000 |
4000 |
25935,892 |
25935,892 |
64,108 |
64,108 |
|
3,10 |
4,671078 |
4,9477 |
5,8755 |
303975 |
4000 |
4000 |
4000 |
25934,789 |
25934,789 |
65,211 |
65,211 |
|
3,15 |
4,580723 |
4,8500 |
5,8269 |
303975 |
4000 |
4000 |
4000 |
25933,652 |
25933,652 |
66,348 |
66,348 |
|
4,00 |
3,208974 |
3,3670 |
5,0015 |
303975 |
4000 |
4000 |
4000 |
25907,723 |
25907,723 |
92,277 |
92,277 |
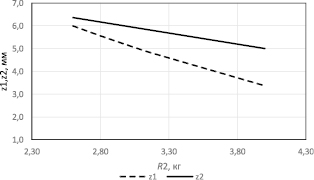
Рис. 3. График зависимости координат положения подвижных элементов (z1, z2) от величины затяжки пружины (R2)
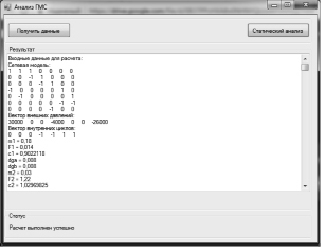
Рис. 4. Программное обеспечение для расчета сетевой модели АДТ
5. Вычисляется величина d1, из которого определяется f1(z1), и перемещение подвижного элемента z1.
6. Определяется величина затяжки пружины R1 по формуле 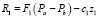 .
.
Результаты моделирования
В результате расчета статического режима получены следующие значения, приведенные в табл. 2, для заданной величины затяжки пружины R2.
В результате построен график зависимости координат положения подвижных элементов (z1, z2) от величины затяжки пружины (R2).
На графике (рис. 3) видно, что координаты положения подвижных элементов (z1, z2) расходятся в зависимости от увеличения величины затяжки пружины.
Для того, чтобы рассчитать данные работы сетевой модели АДТ, было разработано программное обеспечение (ПО) с помощью Visual Studio 2015 (рис. 4), в данном ПО возможно загрузить данные с матрицей инциденций, входные данные и провести статический анализ для заданных значений R2.
Заключение
В результате был проведен анализ работы гидромеханического АДТ в статическом режиме с помощью метода сетевых моделей. Представлена схема сложного АДТ в виде графа и систем уравнений, а также проведены расчеты. Использована теория графов для представления конструкторской схемы АДТ в виде матриц. Разработано ПО, на основе которого проведены расчеты статического режима работы АДТ. Подход расчета параметров АДТ сетевыми моделями и его представление в матричном виде согласуется с матричным представлением режимов работы двигателя [5]. Такой единый подход к объекту управления САУ СУ в будущем планируется использовать на полунатурном стенде и в дальнейшем исследовании взаимной работы АДТ и двигателя с целью повышения качества управления.
Библиографическая ссылка
Бикташева А.Д., Денисова Е.В., Черникова М.А. МЕТОДИКА РАСЧЕТА СТАТИЧЕСКОГО РЕЖИМА РАБОТЫ ГИДРОМЕХАНИЧЕСКОГО АГРЕГАТА ДОЗИРОВАНИЯ ТОПЛИВА НА ОСНОВЕ СЕТЕВОГО МЕТОДА // Фундаментальные исследования. 2017. № 6. С. 31-35;URL: https://fundamental-research.ru/ru/article/view?id=41543 (дата обращения: 24.01.2026).



