Применение листовых материалов в машиностроении, судо- авиа- и ракетостроении, а также в строительном и швейном производстве связано с решением геометрических задач по построению формообразующих поверхностей [1] и разверток их элементов, что позволяет выполнять предварительно крой плоских заготовок с дальнейшим их изгибанием и стыковкой по линиям кроя. В большинстве случаев развертка элементов формообразующих поверхностей выполняется численными методами [4, 6–8]. Обзор некоторых частных аналитических и графических методов развертывания поверхностей можно найти в работе [2].
Линейчатыми называются поверхности, образуемые совокупностью прямых, зависящих от одного параметра [3]. Линейчатую поверхность можно получить движением прямой (образующей) по некоторой линии (направляющей). Примерами линейчатых поверхностей, в частности, являются цилиндры и конусы. Линейчатые поверхности подразделяются на развертываемые и косые. Как известно, развертываемые линейчатые поверхности могут быть посредством изгибания наложены на плоскость без складок и разрывов. Они характеризуются тем, что касательная плоскость в различных точках образующей в каждом ее положении неизменна. Известно также, что линейчатая поверхность тогда и только тогда является развертываемой, когда ее полная (гауссова) кривизна равна нулю [5]. Это эквивалентно условию
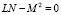 ,
,
где L, M и N – коэффициенты второй дифференциальной формы поверхности.
Этому условию удовлетворяют следующие поверхности, которые представим в параметрической форме:
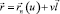 – цилиндрическая поверхность,
– цилиндрическая поверхность,
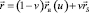 – коническая поверхность,
– коническая поверхность,
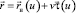 – поверхность касательных (торсовая поверхность).
– поверхность касательных (торсовая поверхность).
Здесь 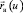 – радиус-вектор точек направляющей кривой,
– радиус-вектор точек направляющей кривой, 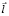 – единичный вектор образующей цилиндрической поверхности,
– единичный вектор образующей цилиндрической поверхности, 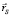 – радиус-вектор вершины конуса,
– радиус-вектор вершины конуса, 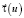 – единичный вектор касательной к направляющей кривой.
– единичный вектор касательной к направляющей кривой.
В данной работе рассмотрены общие алгоритмы построения кривых (линий кроя) на плоскости развертки, в которые трансформируются кривые, принадлежащие перечисленным поверхностям. Эти алгоритмы могут быть легко импортированы в существующие компьютерные математические и графические пакеты при создании соответствующих функций пользователя. Получено также дифференциальное уравнение, описывающее кинематику изгибания пространственной кривой при развертывании поверхности ее содержащей.
Развертывание цилиндрических, конических и торсовых поверхностей
Пусть задана гладкая кривая 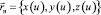 ,
, 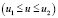 на цилиндрической поверхности таким образом, что один из векторов координатного базиса
на цилиндрической поверхности таким образом, что один из векторов координатного базиса 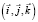 совпадает с вектором
совпадает с вектором 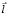 и скалярное произведение
и скалярное произведение 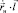 не меняет знак на всей области изменения параметра u. Для определенности положим
не меняет знак на всей области изменения параметра u. Для определенности положим 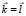 . Найдем уравнение той кривой, в которую трансформируется кривая
. Найдем уравнение той кривой, в которую трансформируется кривая 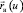 при развертывании цилиндрической поверхности. Введем в рассмотрение декартову плоскость развертки (ξ, η). Тогда одна из координат получаемой кривой определяется как проекция переменной длины заданной направляющей кривой на плоскость, перпендикулярную образующей цилиндрической поверхности, а другая совпадает с пространственной координатой z. То есть
при развертывании цилиндрической поверхности. Введем в рассмотрение декартову плоскость развертки (ξ, η). Тогда одна из координат получаемой кривой определяется как проекция переменной длины заданной направляющей кривой на плоскость, перпендикулярную образующей цилиндрической поверхности, а другая совпадает с пространственной координатой z. То есть
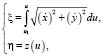
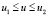 .
.
Пусть задана гладкая кривая 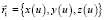 ,
, 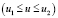 на конической поверхности. Преобразованную кривую, получаемую в результате развертывания конической поверхности, в данном случае удобней искать в полярных координатах
на конической поверхности. Преобразованную кривую, получаемую в результате развертывания конической поверхности, в данном случае удобней искать в полярных координатах
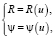
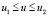 .
.
При этом элементарный полярный угол dψ находим как отношение «приведенной» элементарной дуги 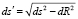 к расстоянию R от произвольной точки кривой до вершины
к расстоянию R от произвольной точки кривой до вершины 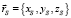 конической поверхности
конической поверхности
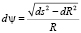
или
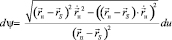 .
.
Уравнения искомой кривой на развертке конической поверхности в параметрической форме принимают вид
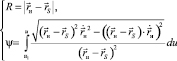 ,
,
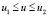 .
.
Рассмотрим бирегулярную направляющую кривую 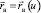 , (
, (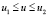 ), являющуюся ребром возврата для поверхности касательных (торсовой поверхности). Найдем уравнения той кривой, которая получится из данной при развертывании поверхности касательных в плоскость. При этом воспользуемся тем, что инвариантами данного преобразования являются длина кривой s(u) и ее кривизна κ(u). С учетом определений кривизн плоских и пространственных кривых находим
), являющуюся ребром возврата для поверхности касательных (торсовой поверхности). Найдем уравнения той кривой, которая получится из данной при развертывании поверхности касательных в плоскость. При этом воспользуемся тем, что инвариантами данного преобразования являются длина кривой s(u) и ее кривизна κ(u). С учетом определений кривизн плоских и пространственных кривых находим
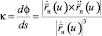
или
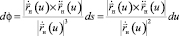 .
.
Введем в рассмотрение плоскость развертки (ξ, η), ось Oξ которой направим по касательной к направляющей кривой в ее начальной точке. Тогда уравнения искомой кривой на плоскости развертки в параметрической форме принимают вид
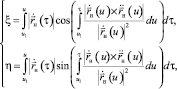
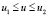 .
.
Кинематика изгибания пространственной кривой при развертывании поверхности ее содержащей
Рассмотрим общий кинематический алгоритм нахождения кривой, в которую преобразуется заданная кривая, лежащая на поверхности при развертывании последней.
Пусть задан кусок регулярной пространственной кривой 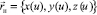 ,
, 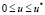 . Запишем общее уравнение линейчатой поверхности в виде
. Запишем общее уравнение линейчатой поверхности в виде
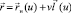 ,
,
где 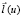 – единичный вектор образующей линейчатой поверхности.
– единичный вектор образующей линейчатой поверхности.
Полагаем, что коэффициенты второй дифференциальной формы поверхности удовлетворяют условию 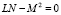 , т.е. заданная линейчатая поверхность – развертываемая и
, т.е. заданная линейчатая поверхность – развертываемая и 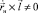 . Предварительно разобьем направляющую кривую
. Предварительно разобьем направляющую кривую 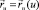 на n частей и заменим ее линейной интерполяцией. Представим алгоритм развертывания этой ломаной линии последовательностью поворотов вокруг осей, заданных единичными векторами
на n частей и заменим ее линейной интерполяцией. Представим алгоритм развертывания этой ломаной линии последовательностью поворотов вокруг осей, заданных единичными векторами 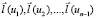 , проходящих через точки разбиения
, проходящих через точки разбиения 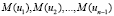 , на углы
, на углы 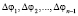 между нормалями к образовавшимся граням (рис. 1).
между нормалями к образовавшимся граням (рис. 1).
Предварительно докажем следующую теорему.
Теорема. Преобразование поворота на угол φ вокруг оси, заданной единичным вектором 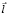 и проходящей через точку M1, переводящее точку M в положение M’ представимо матричным равенством
и проходящей через точку M1, переводящее точку M в положение M’ представимо матричным равенством
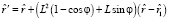 ,
,
где 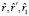 – векторы-столбцы координат точек M, M’ и M1, L – кососимметрическая матрица, определяющая положение оси вращения
– векторы-столбцы координат точек M, M’ и M1, L – кососимметрическая матрица, определяющая положение оси вращения
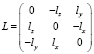 .
.
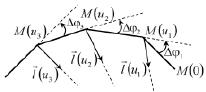
Рис. 1. Схема развертывания линейной интерполяции кривой на разворачивающейся поверхности
Доказательство.
Введем в рассмотрение ось вращения, заданную единичным направляющим вектором 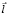 и проходящую через произвольную фиксированную точку M1. Пусть M – положение произвольной точки пространства до вращения, а M’ – ее положение после вращения (рис. 2).
и проходящую через произвольную фиксированную точку M1. Пусть M – положение произвольной точки пространства до вращения, а M’ – ее положение после вращения (рис. 2).
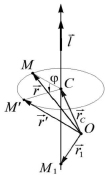
Рис. 2. Схема поворота точки вокруг оси
Рассмотрим точку C пересечения плоскости поворота и оси и представим вектор 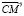 разложением по единичным векторам
разложением по единичным векторам
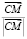
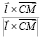 .
.
С учетом равенства 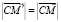 имеем
имеем
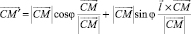
или
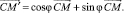 (1)
(1)
При этом
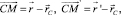
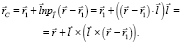
Здесь использована формула вычисления двойного векторного произведения
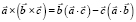 .
.
Тогда равенство (1) может быть переписано в виде
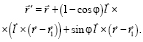
Этому векторному равенству соответствует следующая матричная форма записи
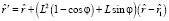 . (2)
. (2)
Теорема доказана.
В случае малого поворота равенство (2) приобретает вид:
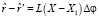 . (3)
. (3)
Для получения алгоритма развертывания регулярной пространственной кривой вместе с содержащей ее поверхностью воспользуемся равенством (3). Для любой точки M(uk) разбиения заданной направляющей кривой можно перейти от векторного представления к матричному 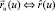 . Перемещения, которые происходят в результате соответствующих поворотов, с учетом равенства (3) описываются системой уравнений
. Перемещения, которые происходят в результате соответствующих поворотов, с учетом равенства (3) описываются системой уравнений
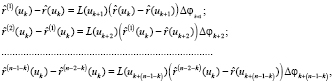 (4)
(4)
где верхний индекс в записи вектора-столбца 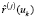 соответствует номеру шага процедуры развертывания.
соответствует номеру шага процедуры развертывания.
Увеличивая количество точек разбиения, дискретное преобразование (4) опишем как непрерывный процесс. Для этого введем в рассмотрение вектор 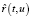 фиксированной точки M(u), (0 ≤ u ≤ u*) кривой
фиксированной точки M(u), (0 ≤ u ≤ u*) кривой 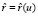 , лежащей на развертываемой поверхности, в положении, соответствующем накопленным поворотам при перемещении оси вращения вдоль кривой и определяемым переменной t, (u ≤ t ≤ u*). Тогда
, лежащей на развертываемой поверхности, в положении, соответствующем накопленным поворотам при перемещении оси вращения вдоль кривой и определяемым переменной t, (u ≤ t ≤ u*). Тогда
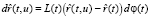 ,
,
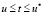 , (5)
, (5)
при краевом условии
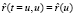 .
.
Отметим, что приращение dφ угла поворота нормали к заданной развертывающейся поверхности в произвольной точке направляющей кривой находится как проекция приращения единичного вектора нормали на касательную к линии кривизны и определяется равенством
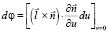
или
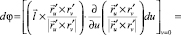
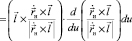 .
.
Дифференциальное уравнение (5) описывает движение произвольной точки M(u) кривой 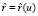 , лежащей на заданной развертываемой поверхности, в процессе развертывания последней.
, лежащей на заданной развертываемой поверхности, в процессе развертывания последней.
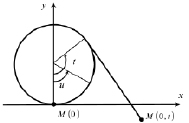
Рис. 3. Схема разворачивания кривой
Проиллюстрируем алгоритм разворачивания кривой на наглядном примере окружности на цилиндре с образующей, параллельной оси Oz (рис. 3). Пусть окружность задана уравнением
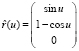 .
.
В этом случае
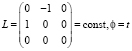
и
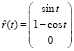 .
.
Записывая уравнение (5) для плоского случая, получим
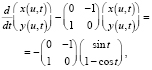
или
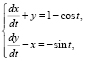
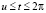 .
.
Решив полученную систему уравнений при краевых условиях
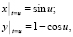
получим
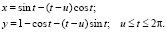
Таким образом, уравнения кривой в промежуточном состоянии ее разворачивания, определяемого параметром t (0 ≤ t ≤ 2π), имеют вид
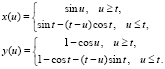
Заключение
С помощью предложенных в работе алгоритмов построены линии кроя, в которые трансформируются кривые, принадлежащие конической, цилиндрической и торсовой поверхности.
В работе получена формула инвариантного поворота трехмерного евклидова пространства относительно оси произвольного направления и проходящей через произвольную точку пространства. Описана кинематика изгибания пространственной кривой при развертывании поверхности ее содержащей. Предложенные методы и алгоритмы могут быть использованы при решении разнообразных задач создания пространственных конструкций в строительстве и промышленности, например при изготовлении натяжных тентовых и листовых пространственных конструкций.
Библиографическая ссылка
Берестова С.А., Беляева З.В., Мисюра Н.Е., Митюшов Е.А., Рощева Т.А. МАТЕМАТИЧЕСКИЕ АЛГОРИТМЫ КРОЯ РАЗВЕРТЫВАЮЩИХСЯ ЭЛЕМЕНТОВ ПРОСТРАНСТВЕННЫХ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ // Фундаментальные исследования. 2017. № 6. С. 26-30;URL: https://fundamental-research.ru/ru/article/view?id=41542 (дата обращения: 28.02.2026).



