Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Рецензия
• Файлы
• Ключевые слова
• Литература

Аль-Хашеди А.А. 1 Обади А.А. 1 Нуриев Н.К. 1 Печеный Е.А. 1

---

1 ФГБОУ ВО «Казанский национальный исследовательский технологический университет»

В статье рассматривается предметная область с конечным множеством различных объектов. Каждый объект имеет конечное множество себе подобных экземпляров. Любой объект из предметной области однозначно характеризуется конечным множеством признаков. При этом два различных объекта могут иметь общие признаки. Вся предметная область в целом характеризуется набором признаков входящих в нее объектов. В работе рассматриваются две взаимосвязанные задачи: задача 1, задача 2. В задаче 1 требуется разбить всю предметную область на классы объектов, т.е. представить её как объединение классов объектов. Для решения этой задачи разработана математическая модель и соответствующий алгоритм процедуры разбиения, который позволяет исходя из размерности признаков объекта и их содержания выделить отдельные классы объектов в предметной области. После установления всех классов в предметной области рассматривается задача 2, построения математической модели и алгоритма распознавания экземпляра объекта с точки зрения принадлежности его какому-то классу объектов предметной области. Эта задача решается на основе Байесовского подхода, т.е. с использованием формул полной вероятности и Байеса. Для разъяснения процедур классификации и распознавания в работе приводится пример использования предложенных алгоритмов.

Рецензия № 1

1800 KB

Рецензия № 2

1515 KB

Статья в формате PDF

0 KB

распознавание образов

коммуникационные услуги

классификация

математическая модель

класс

признак

объект

вероятность

теорема Байеса

1. Лепский А.Е. Математические методы распознавания образов / А.Е. Лепский, А.Г. Броневич. – Таганрог: Курс лекций, 2009. – 155 с.

2. Патрик Э.А. Основы теории распознавания образов / Пер. с англ.; под ред. Б.Р. Левина. – М.: Советское радио, 1980. – 407 c.

3. Потапов A.C. Распознавание образов и машинное восприятие: общий подход на основе принципа минимальной длины описания. – СПб.: Политехника, 2007. – 548 с.

4. Чабан Л.Н. Теория и алгоритмы распознавания образов / Л.Н. Чабан. – М.: Учебное пособие, М.: МИИГАиК, 2004. – 70 с.

5. Goswami J.C. Fundamentals of wavelets. Theory, algorithms, and applications / J.C. Goswami, A.K. Chan. – Wiley, 2000. – 359 р.

Цель работы

Решить две взаимосвязанные задачи: ЗАДАЧА 1 – разработать математическую модель и алгоритм вычислительной процедуры, который позволял бы классифицировать объекты из одной предметной области, исходя из их свойств (признаков), при условии, что часть признаков разных объектов могут совпадать. ЗАДАЧА 2 – на основе вероятностного подхода построить модель и алгоритм вычислительной процедуры, позволяющий идентифицировать принадлежность экземпляра объекта определенному классу из предметной области.

Постановка задачи

Данное U множество образов коммуникационных задач с общими признаками 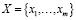, m – количество признаков предметной области (в приведенном ниже примере 1 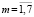, рис. 1). Это множество необходимо разделить на подмножества признаков, соответствующие классам запросов задач данной предметной области. Система составляет словарь признаков с помощью списка правил [1]. Это множество будем обозначать через X. Пока не поступила первая услуга на систему, существует только один общий класс ω, область предпочтения которого является X. Во множестве образов коммуникационных задач предметной области U нас интересуют некоторые подмножества – класс в зависимости от типов коммуникационных услуг. Множество классов Ω = {ω₁,..., ω_m }, является конечным (в данной задаче распознавания 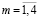и равно числу классов услуг: ω1 – класс услуг интернета, ω2 – класс услуг тарифов, ω3 – класс услуг оплаты, ω4 – класс услуг поддержек), эти классы образуют полную группу подмножеств из U (разбиение множества образов U), т.е. 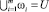, и 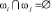. для всех i ≠ j. Классифицировать объект x∈U по классам ωi значит найти такую индикаторную функцию g: U → Y, которая ставит в соответствие образу x∈U метку y_i∈Y того класса ω_i, которому он принадлежит т.е. g(x) = yi, если 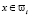, где Y = {yi}, а yi признаки объекта.

Система автоматически создает классы с помощью решающих функций при распознавании поступающих на систему неизвестных образов. В системе количество классов увеличивается с разбиением множества признаков предметной области на подмножества классов в зависимости от появляющихся услуг, и эти классы могут пересекаться между собой, обладая общими признаками [5].

Пусть на систему появилась не идентифицированная услуга x, для которой по своим описывающим признакам 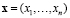, n ≤ m, n – количество признаков задачи, для данной услуги необходимо создать новый класс из множества признаков предметной области 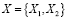. Эта услуга описывается некоторыми признаками в данной предметной области. Эти признаки сравняются с признаками предметной области на совпадение. Если все эти признаки полностью совпадают или с большой вероятностью совпадают с некоторыми признаками предметной области 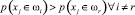, то создается новый класс ω_i. Если большинство признаков совпадают, но не все признаки, то в предметной области выводятся новые признаки и создается новый класс. В случае, когда появляется новая задача и в предметной области уже существуют некоторые классы , то данная услуга проверяется на принадлежность некоторому из существующих классов, если данные признаки совпадают с признаками некоторого класса, то данная задача относится к данному классу. Но если признаки описывающие данную задачу не совпадают или вероятность совпадения 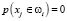с признаками существующих классов, то проверяется на совпадения с общими признаками предметной области, чтобы создать новый класс в данной предметной области.

Алгоритм образования новых классов

На рис. 1, блок А, показано, что X1 – область предпочтения первого класса ω1, а X2 – область предпочтения второго класса ω2. 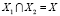– общие признаки. 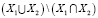– унифицированные признаки. И так далее при поступлении новых услуг в систему создаются новые классы.

На рис. 2 процедура выполнения данного алгоритма следующая:

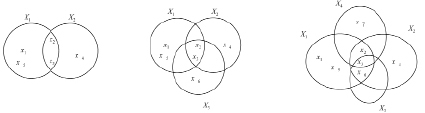
1. В блоке 1, А является обучающая выборка объектов, в которой определяются правила выбора признаков и конечное число количество признаков данной предметной области. Множество X является совокупностью признаков предметной области, составляющейся из m признаков (в приведенном ниже примере 1 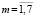, рис. 1), x – вектор признаков распознаваемого образа, образующийся из n признаков и обычно n < m.

2. В блоке 2 сравняется m с n, если m = n, то множество остается таким и задача (распознаваемый образ) относится к общему классу.

а б в

Рис. 1. Разбиение множества признаков на подмножества классов

3. В блоке 3, если n < m, то для сравнения определяется начальный признак множества предметной области i = 1 и начальный признак распознаваемого образа j = 1, и начинается сравнение начального признака распознаваемого образа на совпадение со всеми признаками множества предметной области начинается с первым. Если не совпадают с первым признаком предметной области, то сравнение на совпадение будет с вторым признаком предметной области i + 1 и т.д. до того, как найдётся совпадающий элемент в множестве признаков или i станет равным m (i = m), т.е. признак распознаваемого элемента сравняется со всеми признаками предметной области с первого признака i = 1 до последнего i = m. Затем на сравнение берем следующий признак распознаваемого образа j + 1, данный признак будем сравнивать на совпадение со всеми признаками предметной области и т.д. до того момента когда j = n (рис. 2).

4. В блоке 4. После сравнения всех признаков и условие того, что признаки распознаваемого образа совпадают с признаками в данной предметной области, выполняется т.е. x_j = x_i, то множество предметной области разбивается и появится новый класс ω_i и 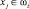. Появление нового класса зависит от значения вероятности совпадения признаков распознаваемого образа с признаками множества предметной области .

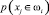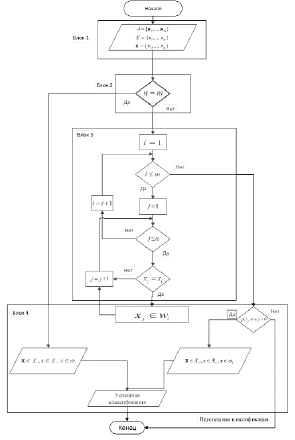
Рис. 2. Логическая блок-схема алгоритма классификации предметной области

Пример классификации с помощью решающих функций

Одной из основных задач распознавания образов является задача описывания классов [1]. Как отметили выше, у нас имеются 4 класса коммуникационных услуг и каждый класс описывается некоторым набором признаков в множестве признаков, например класс интернета описывается следующими признаками: {x1 – интернет, x2 – номер телефона, x3 – название компании и т.д.}. А каждый образ x описывается некоторым набором признаков в множестве признаков – вектором x. Все множество признаков X разбивается на m + 1 попарно несовместных множеств (полную группу множеств, в зависимости от классов) [1, 3, 4], 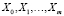: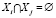, для всех i ≠ j в случае непересекающихся классов, а в случае пересекающих классов может быть такое равенство 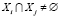как на рис. 1, 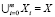. Каждое множество Xi, является множеством предпочтения одного класса ω_i в множестве X, рис. 1. Таким образом, классами распознаваемых образов будем считать области X_i ().

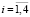Автоматическое определение принадлежности объектов к классам – одна из основных задач теории распознавания образов [1, 2, 4]. Принадлежность распознаваемых объектов можно определять с помощью решающей функции.

Будем считать, что пространство признаков является конечным множеством. В этом случае предполагается, что существует m + 1 функции d_j(x) так, что Xj = {x∈X: d_j(x) > 0}. Можно считать, что образ x принадлежит классу ω_i, если выполняется неравенство d_j(x) < 0 для всех j ≠ i и d_i (x) > 0. Решающей называют функцию вида

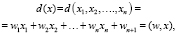
где x = (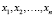, 0) вектор признаков, а (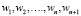) вектор весовых коэффициентов, линейных решающих функций 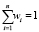[1–3].

Пример 1: пусть на систему поступила такая задача (Set up mobile internet, phone number: +967774541452, model: Apple iPhone 4S, phone carrier: GSM, operating system: IOS). Данную задачу будем считать объектом со следующим вектором признаков

x1 – Set up, x2 – phone number, x3 – model, x4 – operating system, x5 – mobile, x6 – internet, x7 – phone carrier).

Для того чтобы определить решающую функцию каждого класса, будем считать предикаты всех признаков способом сравнения этих признаков с признаками пространства предметной области или с помощью булевых значений таблицы истинности, таким образом если 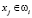т.е. признак объекта соответствует какому-то признаку класса ω_i, 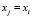, то P(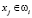) = 1, а если 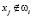т.е. признак распознаваемого объекта не соответствует никакому признаку класса ω_i, то P(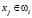) = 0.

На рис. 1 в блоке C множество признаков X разбивается на 4 группы подмножества признаков .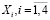

,

,

,

.

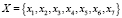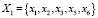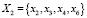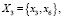
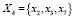Результат вычисления предикатов:

,

,

,

,

,

,

.

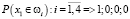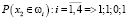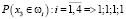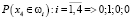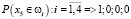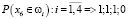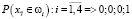Поставим 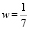, тогда решающая функция будет иметь такой вид:

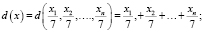
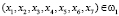, тогда получаем решающую функцию первого класса в таком виде:

;

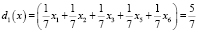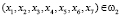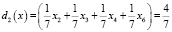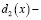, ; решающая функция второго класса;

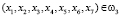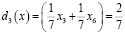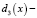, ; решающая функция третьего класса;

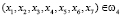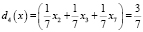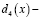, ; решающая функция четвертого класса.

Будем считать, что данный объект x принадлежит классу ω_i в таком случае, если di(x) > 0 = z и 0 < dj(x) < z для всех i ≠ j. Другими словами если di(x) > dj(x), то x принадлежит классу ω_i.

Однако можно считать вероятность принадлежности объекта одному классу условной вероятностью. Будем считать, что x принадлежит классу ω_i, если выполняется следующее условие:

,

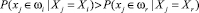для этого вычисляется общая вероятность принадлежности признаков всем существующим классам, как показано в приведенном ниже примере 2.

Пример 2. Hi событие, что 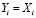, где Yi признаки образа x, а Xi – признаки i-ого класса ω_i, т.е. признаки распознаваемого объекта соответствуют признакам i-ого класса, A событие, что x∈ω_i (объект x принадлежит i-тому классу ω_i). Событие A может произойти только при выполнении события 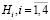. Вероятность P(Hi) того, что 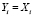, равна произведению вероятности Р(А) того, что x∈ω_i, на вероятность 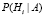того, что причиной события стало именно, что 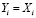(событие Hi), а не другая причина. В данном примере:

P(Hi) = 0,25, вероятность того что данный образец принадлежит i-тому классу, так как у нас имеются 4 класса, т.е. вероятность что данный объект принадлежит одному классу

.

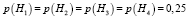Через полученные значения предикатов в примере 1, вероятности выполнения события 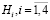, при условии A будут равны следующим значениям:

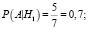
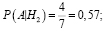
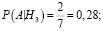
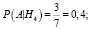
Р(А) – полную вероятность наступления события A вычислим по формуле

,

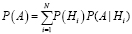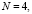
тогда

=

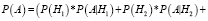
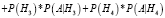= (0,25 * 0,7 + 0,25 * 0,57 + 0,25 * 0,28 + 0,25 * 0,4) = 0,487.

По формуле Байеса получим

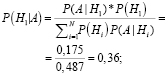
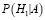– вероятность того, что объект x принадлежит первому классу, именно потому, что его признаки соответствуют признакам данного класса.

;

;

.

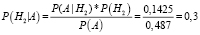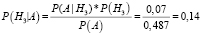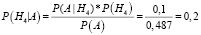Вычисленные вероятности по формуле Байеса нам позволяет сократить перебор классов. Для этого проранжируем по убыванию значения вероятности, т.е.

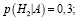
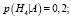
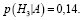
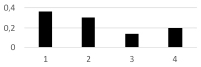
Рис. 3. График вероятностей принадлежности объекта i-тому классу ω_i,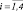

Рис. 4. Блок-схема алгоритма определения порядка идентификации

Идентификацию принадлежности события A определенному классу будем проверять в последовательности ω1, ω2, ω4, ω3.

Заключение

Решена задача 1, т.е. разработаны математическая модель и алгоритм вычислительной процедуры, который позволяет нам классифицировать объекты из одной предметной области, исходя из их свойств (признаков), при условии, что часть признаков разных объектов могут совпадать.

Решена задача 2, т.е. на основе вероятностного подхода построены модель и алгоритм вычислительной процедуры, позволяющий идентифицировать принадлежность экземпляра объекта определенному классу из предметной области.

В заключение следует отметить, что предложенный алгоритм можно использовать для решения задач большой размерности, что является их преимуществом перед множеством известных простых методов классификации.

Библиографическая ссылка