Возможности и перспективы интерактивного обучения детей с помощью мобильного робота
Социальное взаимодействие выступает как важный фактор, значительно влияющий на эффективность процесса обучения детей. Взаимодействие «человек – робот» может рассматриваться как конкретный тип социального взаимодействия, где социальные роботы создаются с целью применения в различных ситуациях, нацеленных на обучение, развлечение, поддержание безопасности человека и его здоровья. Роботы, используемые в социальном взаимодействии с людьми, отличаются несколькими важными особенностями. Одной из наиболее важных особенностей является наличие у ребенка реального партнера по взаимодействию, а не виртуального компьютерного соперника [15]. Второй важной характеристикой робота является наличие у него социального интеллекта. Такие роботы демонстрируют человекоподобный социальный интеллект, основанный на глубинных моделях человеческих познавательных способностей и социальной компетентности [4].
В наше время применение социальной робототехники в обучении детей приобретает все большую популярность. Роботы используются в современных образовательных технологиях для личностного и интеллектуального развития, для усовершенствования процесса обучения и улучшения успеваемости учащихся [8]. В процессе обучения робот может выполнять различные роли в решении учебной задачи: пассивную роль – быть средством обучения; роль равноправного партнера, где предполагается активное и непосредственное участие в деятельности, или роль наставника, когда робот адаптирует упражнения под уровень успеваемости учащегося [12]. Сегодня социальные роботы уже используются в техническом, в естественнонаучном и в языковом направлениях. Обучение с помощью роботов различным математическим компетенциям является перспективной и приобретающей все большую популярность технологией [9].
Эффективность тренингов на основе воплощенного числового познания при обучении детей математике
Основная идея воплощенного познания числовых величин (embodied numerical cognition) [6] в целом основана на предположении, что между чувственно-моторным опытом и поведением существует сложная связь, так как двигательная система не только контролирует и отслеживает действия, но также оказывает влияние на формирование когнитивных представлений, в том числе на представления о числах. Таким образом, телесный опыт системно и функционально влияет на процесс усвоения математических понятий и оперирования числами и арифметическими операциями [7].
Наглядным примером использования воплощенного познания числовых величин в обучении счету является использование детьми пальцев рук для усвоения и усовершенствования вычислений в пределах от 1 до 10 [3]. Движения всего тела также можно рассматривать в качестве примера пространственно-числовых ассоциаций, формируемых в процессе воплощенного числового познания [11]. Наиболее общая идея заключается в том, что движение тела в направлении слева направо связано с формированием и развитием пространственных представлений о числовых величинах.
Одним из вариантов пространственно-числовых ассоциаций является ментальная числовая линия [3]. Основные положения концепции ментальной числовой линии констатируют, что: (1) числа представлены в порядке возрастания, т.е. слева направо относительно числовой линии в большинстве европейских стран: малые числа связаны с левой стороной, а большие числа с правой стороной пространства, в зависимости от их положения на числовой линии [5]; (2) концепт «ментальная числовая линия» начинает формироваться достаточно рано в детском возрасте; тогда как точность определения положения числа на линии возрастает с опытом [13]; (3) умение максимально точно определять положение числа на числовой линии можно тренировать; и успешность выполнения задания на определение положения числа на линии положительно коррелирует с успешностью освоения базовых арифметических операций сложения и вычитания [10].
Уровень сформированности компетенции «числовая линия» у детей можно выявлять с помощью практического задания, в ходе которого предполагается определение положения числа на числовой линии. В решении таких задач дети должны определить пространственное положение заданного числа (например, числа 55), отметив его на числовой линии, на которой отмечены только конечные точки (например, «0» и «100») [14]. Расстояние между отмеченным ребенком и фактическим положением заданного числа на линии является показателем точности его пространственно-числового представления. Точность пространственных представлений чисел рассматривается как надежный показатель хороших математических способностей [10].
В настоящее время тренинги для усовершенствования математических навыков с применением движения вдоль числовой линии в сочетании с элементами воплощенного познания числовых величин приобретают все большую популярность. Дети во время движения слева направо вдоль числовой линии усваивают на сенсорном уровне, что большие числа требуют перемещения на большие дистанции по сравнению с малыми числами, когда достаточно сделать несколько шагов. На основе идеи воплощенного познания числовых величин были разработаны системы занятий для детей, направленные на развитие пространственно-числовых ассоциаций в диапазонах от 0–10 до 0–100 с использованием различных цифровых средств: танцевального коврика, интерактивной доски, датчика Xbox Kinect [7; 10]. Развивающие занятия на основе воплощенного познания числовых величин оказались эффективными для разных возрастных групп, начиная от дошкольников и заканчивая учащимися 2 класса. Тренируемые навыки соответствовали тем математическим компетенциям, которые изучаются в соответствующем возрасте (начиная со сравнения однозначных чисел в детском саду и заканчивая определением пространственно-числовой зависимости во 2-м классе).
Модель интерактивного пространственно-числового тренинга с использованием мобильного робота
Рассматривая пространственные представления чисел как мощный инструмент для обучения детей счету, при разработке модели интерактивного тренинга базовых математических компетенций мы опирались на такие концептуальные положения, как:
– пространственно-телесные переживания при усвоении чисел и арифметических понятий способствуют познавательной активности и закрепляют усвоенные математические знания;
– концепт «числовая линия» является мощным инструментом понимания и усвоения пространственного кодирования чисел слева направо;
– тренинги, направленные на формирование пространственно-числовых представлений, являются полезными для усовершенствования базовых арифметических навыков у детей: сравнение простых чисел, определение разрядности цифры в двузначных числах, сложение и вычитание чисел.
Таким образом, разрабатываемая модель интерактивного тренинга базовых математических компетенций предполагает применение пространственно-числового тренинга на основе воплощенного познания числовых величин в условиях социального взаимодействия с роботом. Интерактивное обучение ребенка будет осуществляться в форме активной игры-соревнования с социальным роботом с целью выполнения различных арифметических заданий на числовой линии. Мобильный робот будет выступать в качестве равноправного партнера при выполнении одинаковой задачи – передвижения вдоль числовой линии к определенному числу с целью фиксирования заданного или полученного числа на ней.
Разработка аппаратной части мобильного робота
Функционально, устройство роботизированной числовой линии состоит из четырех подсистем, связанных между собой по беспроводному каналу передачи информации и работающих в режиме «одно ведущее устройство и три ведомых»:
- подсистема изображения элементов числовой линии посредством лазера;
- лазерный дальномер с функцией сканирования по азимутальному углу;
- конкурентное мобильное робототехническое устройство;
- центральное устройство управления отдельными подсистемами.
Подсистема изображения элементов числовой линии представляет собой независимое устройство с одним или несколькими лазерными модулями разных цветов (зеленый или красный), с функцией включения и выключения в фиксированные промежутки времени, а также возможностью поворота лазерного луча (или лучей) в двух плоскостях посредством системы зеркал с целью получения растра с рисунком линии и ее отдельных элементов. Устройство располагается над рабочим полем на штативе или потолке таким образом, чтобы лазерные лучи светили на пол и чтобы при перемещении ребенка и (или) робота не происходило их прерывание.
Подсистема лазерного дальномера предназначена для отслеживания текущего местоположения ребенка и робота вдоль числовой линии и для содействия в навигации мобильного робототехнического устройства. С целью обеспечения контроля одновременно двух объектов в ней предусмотрена возможность управления азимутальным углом лазерного луча, с помощью которого определяется расстояние до одного из двух объектов. Подсистема лазерного дальномера располагается на жесткой поверхности вдоль числовой линии на высоте трех десятков сантиметров от уровня пола. При этом содействие в навигации для робота заключается в том, что мобильный робот посредством оптических навигационных датчиков может регистрировать попадание лазерного излучения на тело, и соответственно корректировать свое направление движения, в случае если траектория перемещения по каким-либо причинам начинает отличаться от параллельной числовой линии.
В обеих подсистемах мощность лазерного излучения выбирается исходя из требований безопасности. Также дополнительно, могут быть использованы защитные очки.
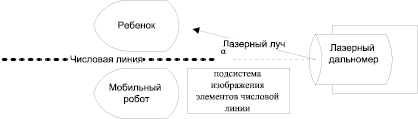
Рис. 1. Расположение отдельных подсистем на рабочем поле
Подсистема центрального устройства управления обеспечивает согласованное взаимодействие входящих в комплекс подсистем и задание режимов и сценариев работы, в том числе регистрацию и обработку навигационных данных о расстояниях до объектов и углы их расположения, настройку параметров отображения числовой линии и прочее. Расположение отдельных подсистем на рабочем поле представлено на рис. 1.
В качестве конкурентного мобильного робототехнического устройства, предназначенного для перемещения вдоль числовой линии совместно с ребенком, используется автономная униколесная трехприводная роботизированная платформа с возможностью движения в произвольном направлении. Ее конструкция содержит 3 колеса, расположенные под углом 120 градусов друг относительно друга, приводимые в движение шаговыми приводами. Каждое колесо может перемещаться по плоскости как относительно центральной оси вращения, так и ортогонально, посредством радиальной системы подвижных роликов.
Фотография представлена на рис. 2.

Рис. 2. Мобильное робототехническое устройство для числовой линии с возможностью произвольного перемещения
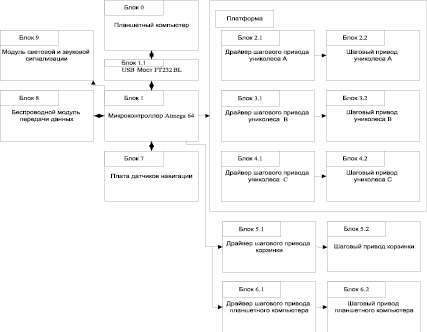
Рис. 3. Структурная схема системы управления мобильным роботом
Структурная схема системы управления роботом представлена на рис. 3.
Основой системы управления является бюджетный микроконтроллер Atmega64 [2] (блок 1). Управление шаговыми приводами [1] колес платформы (блок 2.2, блок 3.2, блок 4.2) осуществляется посредством драйверов (блок 2.1, блок 3.1, блок 4.1). Управление шаговыми приводами перемещения корзинки (блок 5.2) и планшетного компьютера (блок 6.2) осуществляется посредством драйверов (блок 5.1, блок 6.1). Определение текущего местоположения осуществляется с использованием платы навигации (блок 7). В ее состав входят датчики: магнитный компас, 3 ультразвуковых датчика расстояния и оптический датчик черной линии. Связь с планшетным компьютером осуществляется посредством периферийного моста (блок 1.1). Обмен данными с внешним устройством управления осуществляется посредством беспроводного модуля (блок 8). Световая и звуковая сигнализация реализована посредством модуля 9.
3-D модель печатной платы контроллера системы управления, а также собранный контроллер представлены на рис. 4, а и б соответственно.

а

б
Рис. 4. Фотография 3d модели печатной платы контроллера системы управления и контроллера в сборе
Заключение
В современном мире популярность и значимость социальной робототехники в обучении растет. Применение мобильных роботов в интерактивном обучении математическим компетенциям является перспективной и активно развивающейся технологией, достоинствами которой являются привлекательный игровой дизайн, наличие у ребенка реального, а не виртуального партнера по взаимодействию, невозможность полностью вычислить действия мобильного робота (его скорость и точность действий, правильность ответов на математические задания). Технология интерактивного обучения с помощью мобильных роботов предполагает эффективное сочетание с воплощенным познанием числовых величин и применением числовой линии. Таким образом, в нашем проекте взаимодействие робота и ребенка будет осуществлено в форме игры-соревнования с целью выполнения различных заданий на числовой линии. Мы предполагаем, что пространственно-числовые тренинги на основе воплощенного познания числовых величин, комбинированные с социальным взаимодействием в игровой форме, покажут высокую эффективность их применения в качестве нового и увлекательного для детей способа обучения счету.
Предложенная аппаратная реализация числовой линии для обучения детей счету предназначена для использования в автономном режиме, обладает приемлемыми технико-экономическими характеристиками и не имеет особых требований к помещению для осуществления тренинга. Примененное решение навигации, в основе которого используется лишь один лазерный дальномер, позволяет исключить дорогостоящие модули технического зрения, отвечающие за обработку видеоизображений. Использование системы лазерного отображения числовой линии делает комплекс более гибким и удобным в использовании. При этом появляется возможность формировать базы сценариев и различных модификаций изображений.
Работа выполнена в рамках проекта № 2014/420-723 «Разработка конструкции, технологии изготовления и программного обеспечения мобильного робототехнического устройства».
Библиографическая ссылка
Ситникова М.А., Афонин А.Н., Алейников А.Ю., Гладышев А.Р., Попова А.В. ИСПОЛЬЗОВАНИЕ МОБИЛЬНОГО РОБОТА ДЛЯ ИНТЕРАКТИВНОГО ОБУЧЕНИЯ СЧЕТУ С ПОМОЩЬЮ ЧИСЛОВОЙ ЛИНИИ // Фундаментальные исследования. 2017. № 5. С. 72-77;URL: https://fundamental-research.ru/ru/article/view?id=41510 (дата обращения: 11.03.2026).



