Изменения, происходящие на рынке нефти, вызывают острую потребность в оптимизации деятельности нефтеперерабатывающих заводов (НПЗ) для поддержания конкурентоспособности. Существенный вклад в повышение эффективности производства вносят методы исследования операций [3]. При этом одним из важных аспектов работы завода является обеспечение жизненно важной обратной связи производства и отгрузки нефтепродуктов для постоянной переоценки работы производственно-сбытовых цепочек и производительности установок. Системный анализ работы производства, приема и отгрузки нефтепродуктов, работы терминалов в рамках единой системы дает существенный синергетический эффект [1, 7, 9].
Для увеличения операционного дохода за счет оптимизации загрузки производственных мощностей широко используются модели оптимального планирования, основанные на применении математических моделей линейного программирования (LP-моделях), такие как PIMS (компания «AspenTech»), RPMS (компания «Honeywell») и другие [4, 9]. Поступление сырья и отгрузка нефтепродуктов входят в структурные ограничения системы уравнений LP-модели НПЗ, являются ключевыми параметрами и существенно влияют на экономические результаты [6, 8].
Отметим, что LP-модели оперируют со средними значениями и не приспособлены к детальному учету реальных производственных ограничений. Возможные сбои, связанные с конъюнктурой рынка, работой транспорта и производством продукции, могут нарушить календарный график, основанный на детерминированной модели, и привести к существенным потерям. Это означает, что рабочие процессы и инструменты планирования должны быть хорошо адаптированы для поддержки различных сценариев в условиях неопределенности. Применение теории систем массового обслуживания (далее СМО) открывает целый ряд новых возможностей использования математического моделирования при решении производственных задач нефтепереработки и отгрузки инновационными способами [9, 10].
Работу погрузочно-разгрузочного комплекса можно рассматривать с позиции СМО [3]. Если поток регулярен и время обслуживания равно интервалу между заявками, СМО справляется с потоком заявок. Но стоит потоку заявок и обслуживанию стать случайными, может возникнуть очередь из поступающих вагонов или нехватка сырья для загрузки установок. То и другое связано с существенными экономическими потерями. Кроме того, неверные ограничения пропускной способности эстакад приводят к ошибочным решениям при расчёте оптимального плана. Построение математической модели СМО, адекватно отражающей исследуемый объект, как известно, является актуальной и нетривиальной задачей [2].
Следующим важным этапом является контроль и прогнозирование работы СМО с последующим принятием управленческих оптимизационных решений. Оптимизация работы СМО позволяет добиться максимальной загрузки эстакад и в то же время не допускать скопления вагонов-цистерн. Поскольку СМО является лишь составной частью производственной цепочки, при прогнозировании данные детерминированной LP-модели и СМО должны быть интегрированы в единую систему. Такой подход включает взаимосвязанное рассмотрение последствий каждого решения и координацию работы между различными участниками процесса.
Целью работы является построение модели СМО для оптимизации и планирования работы железнодорожных эстакад, разработка алгоритмов расчета ограничений для LP-модели оптимального планирования, прогнозирование работы комплекса и расчет графиков приема сырья. Моделирование дает возможность рассчитать вероятность скопления транспорта и снизить затраты, вызванные простоем транспорта или неоптимальной загрузкой завода при недопоставке сырья.
Рассмотрим работу одной эстакады слива. Схема потока сырья приведена на рис. 1. Сырье в вагонах-цистернах поступает на эстакаду, сливается в резервуарный парк и далее направляется для переработки на технологические установки. Действующая схема планирования построена следующим образом: определяется потребность в сырье технологических установок в соответствии с оптимальным планом производства с учетом технологической мощности эстакады, затем составляется график поступления сырья на НПЗ и движение остатков в резервуарных емкостях. Таким образом, происходит увязка логистических и производственных процессов предприятия.

Рис. 1. Схема потока сырья, поступающего на железнодорожную эстакаду слива, в резервуарный парк и на переработку
Помимо классической схемы поступления заявок в декартовой системе координат [3], визуализацию данных для одновременного отображения плановых и фактических значений удобно провести в полярной системе координат. В качестве полярного угла используем время. На рис. 2 на круговой диаграмме изображены типичные результаты работы эстакады слива углеводородного сырья. Задачей является обеспечение приема 10 составов за 12 суток. Диаграмма наглядно иллюстрирует расхождение нормативного и реального времени разгрузки составов и возможность корректировки времени для обеспечения предприятия сырьем в оставшиеся до контрольного срока дни.
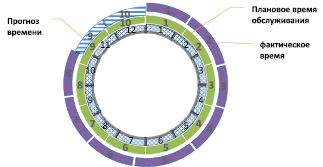
Рис. 2. Диаграмма работы эстакады по приему углеводородного сырья. Внутренняя область показывает время (сутки), средняя область – плановое время с отметками порядковых номеров обслуживаемых составов, внешняя часть – фактическое время обслуживания составов с номерами составов и прогноз времени обслуживания
Из рисунка можно видеть, что за 10 дней работы наблюдается отставание от планируемого времени, для выполнения первоначального графика предлагается осуществить процессы слива в более сжатые сроки. На диаграмме интервалы фактического времени слива представляют собой нерегулярные отрезки времени, штрихом показан план работы до конца периода с постоянным временем слива.
Работу одной эстакады слива углеводородного сырья будем моделировать одноканальной СМО с неограниченной очередью. При моделировании работы эстакад используется модель с формулами Литтла [3]: 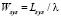 (где Wsys – среднее время пребывания заявки в системе, λ – интенсивность потока заявок, Lsys – среднее число заявок в системе). Отметим, что формула Литтла справедлива для любой СМО, при любом распределении времени обслуживания и любой дисциплине обслуживания.
(где Wsys – среднее время пребывания заявки в системе, λ – интенсивность потока заявок, Lsys – среднее число заявок в системе). Отметим, что формула Литтла справедлива для любой СМО, при любом распределении времени обслуживания и любой дисциплине обслуживания.
При прогнозировании рассмотрим систему массового обслуживания с однородным потоком (все заявки равноправны, рассматриваются только моменты поступления заявок). Поток без последействия, т.е. число событий любого интервала времени 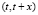 не зависит от поступления заявок до момента t. Считаем, что поток стационарный, т.е. вероятность появления n событий на интервале времени
не зависит от поступления заявок до момента t. Считаем, что поток стационарный, т.е. вероятность появления n событий на интервале времени 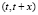 не зависит от времени t, а зависит только от длины x интервала. Для решения задачи будем рассматривать поток Пуассона [3] с параметром λ. Время обслуживания заявок распределено по показательному закону. Таким образом, в работе рассматривается однолинейная система с ожиданием, пуассоновским входным потоком и показательным временем обслуживания, т.е. используется модель
не зависит от времени t, а зависит только от длины x интервала. Для решения задачи будем рассматривать поток Пуассона [3] с параметром λ. Время обслуживания заявок распределено по показательному закону. Таким образом, в работе рассматривается однолинейная система с ожиданием, пуассоновским входным потоком и показательным временем обслуживания, т.е. используется модель 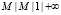 по классификации Кендалла.
по классификации Кендалла.
Обработка фактических данных показала, что гипотезу простейшего потока приходящих на товарно-сырьевое производство железнодорожных составов, так же как и гипотезу показательного распределения длительности разгрузочных операций, в первом приближении можно принять для прогнозирования. В целом случаются задержки, связанные с технологическими операциями на эстакаде и нестабильной работой технологических установок, поэтому для увеличения точности моделирования следует использовать и более сложные модели.
Рассмотрим эвристический алгоритм идентификации и оценки пропускной способности эстакады с учетом случайного характера поступления заявок и времени обслуживания для использования в моделях линейного программирования. В теории СМО вводится понятие номинальной производительности N, для рассматриваемой задачи – это максимальная пропускная способность эстакады, если каждый состав обслуживается точно со средним временем и составы всегда есть в наличии. Фактическая производительность F оказывается меньше этого значения. Тогда коэффициент использования эстакады ηsy, как отношение фактической производительности к номинальной, определяется по формуле 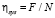 .
.
Процесс слива существенно зависит от ряда факторов: технического состояния эстакады, графика поставки сырья, плана производства, от вязкости нефтепродуктов, которая, в свою очередь, зависит от качества сырья и его температуры. Исходя из текущей ситуации, коэффициент использования эстакады для прогнозирования ηf подбирается эвристически с учетом работы всех объектов, представленных на рис. 1. Проводится корректировка коэффициента ηsys с учетом текущей ситуации экспертным путем (на практике до ± 3 %), вычисляются ограничения максимальной производительности эстакады P по формуле 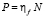 и статистические характеристики СМО. Например, при прогнозировании приема сырья коэффициент ηsys может быть увеличен при увеличении температуры окружающего воздуха, уменьшающей вязкость нефтепродукта во время слива. Структурные ограничения P учитываются в LP-модели при расчете оптимального плана.
и статистические характеристики СМО. Например, при прогнозировании приема сырья коэффициент ηsys может быть увеличен при увеличении температуры окружающего воздуха, уменьшающей вязкость нефтепродукта во время слива. Структурные ограничения P учитываются в LP-модели при расчете оптимального плана.
Таким образом, для расчета ограничений по максимальной загрузке эстакады слива предлагается использовать следующий алгоритм:
1. Определение номинальной производительности N с использованием статистических данных прошлого периода.
2. Расчет коэффициента использования эстакады ?sys.
3. Экспертная корректировка коэффициента ?sys и вычисление ограничения P по максимальной производительности.
4. Построение графика приема сырья с учетом номинальной производительности эстакады, коэффициента ее ηsys и интенсивности потока заявок.
Следующим этапом является применение модели СМО для построения прогноза и календарного графика приема сырья. Расчеты проводятся с применением прикладного программного обеспечения «Logistics Sleeve» [5]. В программе рассматриваются следующие фактические входные данные: время заезда состава на завод, время выезда состава с завода, общее время от подачи до уборки (в том числе время слива), время простоя эстакады, масса поступившего сырья. Данные поступают из ERP-системы в модуль обработки, прогноз выгружается в шаблон MS Excel, в котором автоматически рассчитывается относительная пропускная способность, абсолютная пропускная способность и вероятность отказа по известным формулам [3], имеется возможность построить прогноз и график приема сырья.
Система позволяет контролировать задержку поступления нефтяного сырья, сбои при разгрузке продукции, сверхнормативное поступление сырья. Работа эстакады, запасы и производство при построении прогноза рассматриваются как единая интегрированная система. Анализ результатов моделирования дает возможность рассчитать вероятность возникновения очередей и позволяет принять эффективные управленческие решения при оптимизации работы технологических установок и приема сырья.
Таким образом, моделирование работы эстакады слива с использованием теории СМО позволяет корректно определять ограничения в LP-моделях оптимального планирования, осуществлять прогноз выполнения плана приема сырья и отгрузки продукции, своевременно проводить корректировку плана производства и отгрузки. Анализ характеристик СМО дает возможность выделять проблемные вопросы («узкие места») при работе эстакад.
Обработка реальных данных показала, что модель с использованием СМО является более адекватной по сравнению с детерминированной, которая основана на фиксированной технологической мощности эстакады, поскольку позволяет получить более точный прогноз количества слитого на эстакаде углеводородного сырья.
Экономическая эффективность решений, принимаемых на основе моделирования, достигается за счет сокращения упущенной выгоды при корректных ограничениях в LP-модели для расчета оптимальной загрузки установок завода и снижения издержек от простоя вагонов-цистерн с сырьем. Дополнительные эффекты обусловлены интеграцией данных LP-модели и модели СМО при согласовании графиков производства и отгрузки с предотвращением потерь операционного дохода при некорректном планировании и слабом контроле графиков слива.
Итак, подход на основе теории СМО имеет очевидное преимущество перед методом учёта средних характеристик работы системы, поскольку даёт возможность учесть отклонения от идеального графика работы и внештатные ситуации, такие как задействование резервных возможностей и изменение производительности технологических установок. В работе изложена концепция математического моделирования с использованием теории СМО, которая реализована в программном комплексе по планированию приема сырья по железной дороге. Практическое использование позволяет провести оптимизационные расчеты, прогнозировать максимальную производительность СМО и осуществлять контроль операций, что дает возможность принять меры по снижению затрат, вызванных простоем транспорта, оптимизировать загрузку производственных мощностей. Приведена методология экономической оценки эффективности предложенных решений.
Математическая модель, рассмотренная в работе, носит достаточно общий характер, и ее результаты справедливы для различных отраслей, связанных с планированием и управлением производственными и логистическими цепочками.
Библиографическая ссылка
Кувыкин В.И., Кувыкина Е.В. МОДЕЛИРОВАНИЕ РАБОТЫ ЖЕЛЕЗНОДОРОЖНЫХ ЭСТАКАД НЕФТЕПЕРЕРАБАТЫВАЮЩЕГО ЗАВОДА C ИСПОЛЬЗОВАНИЕМ ТЕОРИИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ // Фундаментальные исследования. 2017. № 4-2. С. 266-270;URL: https://fundamental-research.ru/ru/article/view?id=41472 (дата обращения: 02.02.2026).



