Развитие новых технологий солнечной энергетики [4] инспирирует исследования в области численного моделирования физических свойств светопроводящих материалов с использованием современных CAE-систем инженерного анализа.
Расчетная часть современных CAE-пакетов чаще всего базируется на методе конечных элементов. Как известно, решение задач МКЭ требует дискретизации исследуемого объекта на конечное множество элементов. Требования к точности вычислений подразумевают создание не менее десятка тысяч конечных элементов, поэтому в дополнение к основным расчетным модулям создаются и алгоритмы генерации разбиения.
В настоящее время высокую эффективность построения адаптивных сеток с заданной плотностью на сложной физической области демонстрируют нейросетевые алгоритмы [1–3], в основе которых лежат идеи чередования базового алгоритма [5] SOM для внутренних и внешних узлов сетки, а также усовершенствования функции соседства нейронов.
Применение существующих нейросетевых алгоритмов для задачи синтеза конечно-элементной сетки пространственной области, характеризующейся наличием узких светопроводящих каналов, поперечные размеры которых несоизмеримо меньше размеров области, а длина сопоставима с ее диаметром, приводит к вырезу лишних узлов сети и наличию самопересечений сети на этапе упорядочения.
В данной работе предложены улучшенный композиционный нейросетевой алгоритм построения конечно-элементной сетки пространственной области, характеризующейся наличием узких светопроводящих каналов, длина которых сопоставима с диаметром области, программная реализация и апробация предложенных алгоритмов, рекомендации по выбору параметров обучения.
Краткое описание нейросетевых алгоритмов
Пусть в многосвязной области G выделены внутренние границы 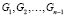 , внешняя граница Gn и внутренность
, внешняя граница Gn и внутренность 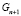 .
. 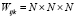 – равномерная кубическая сетка. Подмножество Wn описывает узлы Gn,
– равномерная кубическая сетка. Подмножество Wn описывает узлы Gn, 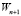 –
– 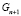 ,
, 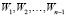 –
– 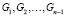 .
.
В этих обозначениях модифицированный алгоритм [2] представлен последовательностью:
1. Устанавливаются начальные веса wijk всех нейронов в вершинах трех-мерной сетки.
2. На первой макроитерации (s = 1) дискретного времени 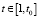 выполняется:
выполняется:
2.1. Генерируется случайная точка x(t) во всей области G.
2.2. Определяется нейрон победитель в евклидовой метрике d. Фиксируются сеточные координаты нейрона победителя 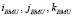 (BMU – best matching unit) для образца x(t).
(BMU – best matching unit) для образца x(t).
2.3. Настраиваются новые весовые значения нейронов сети по формуле
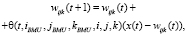 (1)
(1)
где
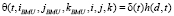 (2)
(2)
– функция соседства нейронов, δ(t) – скорости обучения, 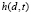 – расстояния.
– расстояния.
3. Осуществление вырезов:
3.1. Удаление нейронов, попавших в полости области G.
3.2. Определение внутренних границ сетки 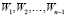 .
.
4. На каждой макроитерации s > 1 выполняется:
4.1. В течение T1(s) итераций:
4.1.1. Генерируется случайная точка x(t) на одной из границ 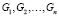 .
.
4.1.2. Определяется BMU из граничных узлов сетки, индексы которых входят в Wi.
4.1.3. Настраиваются новые весовые значения граничных узлов Wi по формуле (1).
4.2. В течение T2(s) итераций:
4.2.1. Генерируется случайная точка x(t) во всей области G.
4.2.2. Определяется нейрон победитель BMU среди всех узлов сетки.
4.2.3. Если в шаге 4.2.2 победил нейрон сетки, индексы которого входят в 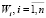 , то случайно сгенерированная точка
, то случайно сгенерированная точка 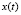 заменяется на этот нейрон.
заменяется на этот нейрон.
4.2.4. Настраиваются новые весовые значения внутренних узлов 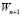 по формуле (1).
по формуле (1).
5. Повторяются макроитерации до тех пор, пока изменения положений узлов не станут достаточно малыми.
Здесь и в работе [2] рассмотрена упрощенная функция соседства (2). За скорость обучения выбрана убывающая степенная функция 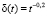 , за функцию расстояния – функция Гаусса
, за функцию расстояния – функция Гаусса 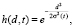 где
где 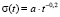 – радиус обучения,
– радиус обучения,
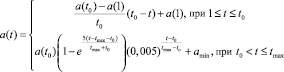 . (3)
. (3)
В представленном алгоритме в качестве расстояния d в формуле (2) используется сеточное расстояние
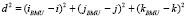 . (4)
. (4)
Постановка задачи
Применение изложенного алгоритма для области, характеризующейся наличием узких светопроводящих каналов, приводит к некачественному построению сети еще на этапе уточнения (рис. 1).
Как видно из рис. 1, при оптимальных значениях радиуса обучения [2] сеть не покрывает всю длину светопроводящих каналов. Значительное уменьшение радиуса обучения исправляет эту ошибку, однако при больших перемещениях характерных для этапа уточнения, это приводит к нарушению гладкости и ухудшению качества построения сети.
Кроме того, на этапе упорядочения в области внутренних границ световых каналов возникают самопересечения сети и артефакты. Это объясняется тем, что латеральные связи произвольной пары узлов внутренней границы 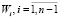 , разделенных узким светопроводящим каналом, остаются такими же сильными, как и для узлов внутренней области
, разделенных узким светопроводящим каналом, остаются такими же сильными, как и для узлов внутренней области  с тем же сеточным расстоянием. Вполне естественно предположить, что при ослаблении латеральных связей между такими узлами можно снизить указанный негативный эффект.
с тем же сеточным расстоянием. Вполне естественно предположить, что при ослаблении латеральных связей между такими узлами можно снизить указанный негативный эффект.
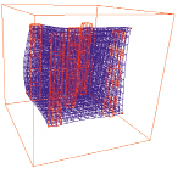
Рис. 1. Итоговое расположение сетки на этапе уточнения
Таким образом, для решения проблемы качественного построения конечно-элементной сетки светопроводящего материала необходимо:
1. Разработать алгоритм, позволяющий покрыть светопроводящие каналы до этапа удаления узлов при условии сохранения оптимального значения радиуса обучения.
2. Разработать способ ослабления латеральных связей между узлами, разделенными узким светопроводящим каналом.
Основные идеи
Для правильной адаптации светопроводящих каналов предлагается ввести дополнительный этап обучения, состоящий в уточнении области относительно внешней границы.
3. Уточнение области относительно внешней границы:
3.1. В течении T1(0) итераций:
3.1.1. Генерируется случайная точка x(t) на внешней границе области G.
3.1.2. Определяется нейрон победитель BMU из граничных узлов Wn.
3.1.3. Настраиваются новые весовые значения граничных узлов по формуле (1).
3.2. В течение T2(0) итераций:
3.2.1. Генерируется случайная точка x(t) во всей области G.
3.2.2. Определяется нейрон победитель BMU среди всех узлов сетки.
3.2.3. Если в шаге 3.2.2 победил нейрон, индексы которого входят в Wn, то случайно сгенерированная точка x(t) заменяется на этот нейрон.
3.2.4. Настраиваются новые весовые значения 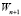 по формуле (1).
по формуле (1).
Данный этап вводится перед удалением лишних узлов сетки при рекомендованных [2] значениях радиуса обучения. Таким образом, в новом композиционном алгоритме выделяются четыре этапа обучения соответствующих предварительному уточнению области, уточнению области относительно внешней границы, удалению лишних нейронов и упорядочения.
Корректировка латеральных связей. Удаление нейрона относительно начальной топологии сети влечет к удалению всех смежных связей нейрона. В измененной таким образом сети уже неестественно использовать формулу сеточного расстояния (4), т.к. она не представляет собой функцию кратчайшего расстояния (рис. 2, а).
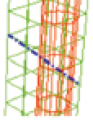
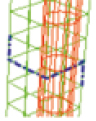
а б
Рис. 2. Схема расчета сеточного расстояния для узлов внутренней границы: а – без учета топологии сети, б – с учетом топологии сети
Изменим функцию d из (4), так чтобы она представляла собой функцию кратчайшего расстояния между двумя узлами сети на многосвязной области (рис. 2, б).
В отличие от односвязной области, определение расстояния между точками многосвязной области не является тривиальной задачей и требует отдельного решения.
Поскольку количество узлов сети конечно, это позволяет поставить задачу в терминах теории графов. В такой интерпретации нейрон – это вершина графа, его связи – ребра. Если для пары узлов существует соединяющий отрезок, лежащий в пределах многосвязной области, соответствующей топологии нейросети, то в графе существует ребро, вес которого равен длине отрезка. Отметим, что построенный таким образом граф, при умеренном количестве вырезов и достаточно большом N, является плотным.
Таким образом, под функцией d будем подразумевать кратчайшее расстояние в графе между вершинами соответствующими узлу-победителю и узлу, выбранному в процессе пересчета весов нейронной сети.
В данной работе для расчета кратчайшего расстояния выбран алгоритм Флойда – Уоршела [4]. Это динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа со сложностью 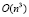 .
.
Расчет кратчайших расстояний в графе осуществляется после удаления узлов, вышедших за границы области.
Результаты вычислений
Вычисления проводились на симметричной выпуклой области G – куб с пятью полыми включениями в форме узких цилиндров, длина которых сопоставима с длиной ребра куба. Полости в форме цилиндров моделируют светопроводящие каналы материала. Выбор симметричной формы светопроводящего материала обусловлен очевидностью выбора правильного расположения конечно-элементной сетки в процессе вариаций параметров обучения и не накладывает никаких ограничений на внешнюю форму материала.
Вычислительные эксперименты показали эффективность введения этапа уточнения внешней границы области (рис. 3).
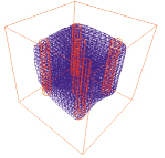
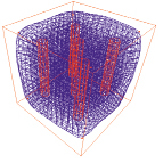
а б
Рис. 3. Расположение нейросети на этапах предварительного уточнения (а) и уточнения внешней границы (б)
На рис. 3, а приведен результат обучения на этапе предварительного уточнения области. Как видно на рис. 3, б, этап уточнения внешней границы полностью исправил ошибку покрытия светопроводящих каналов, сохраняя рекомендуемый [2] достаточно большой радиус обучения (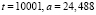 ) для дальнейшего обучения нейросети.
) для дальнейшего обучения нейросети.
Проводился анализ качества построения сети от вариации параметров a – коэффициент радиуса обучения (3) и t – числа итераций на каждой стадии обучения. Результаты хорошо согласуются с работами [1, 2]. Так, уменьшение нижнего предела параметра a(t0) на этапе упорядочивания при неизменных t0 и a(1) приводит к ухудшению качества предварительного построения сетки. Это объясняется тем, что с уменьшением радиуса обучения основное смещение узлов происходит в окрестности сгенерированных точек. В результате нарушается не только гладкость сетки, но и увеличивается ее размер, что значительно ухудшает качество адаптации на этапе упорядочения. Для поставленной задачи положительные результаты построения сети получены при использовании нижнего предела параметра a не ниже 25.
При уменьшении верхнего предела a качество адаптации сетки значительно снижается. Вычислительные эксперименты показали, что при оптимальном значении начального радиуса обучения 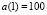 в первых итерациях сеть «сжимается» к случайно сгенерированным точкам, уменьшаясь в размерах. После чего медленно разворачивается, адаптируясь к особенностям области. При уменьшении начального радиуса сеть минует стадию «сжатия», и начальные размеры сети уменьшают возможности правильной адаптации.
в первых итерациях сеть «сжимается» к случайно сгенерированным точкам, уменьшаясь в размерах. После чего медленно разворачивается, адаптируясь к особенностям области. При уменьшении начального радиуса сеть минует стадию «сжатия», и начальные размеры сети уменьшают возможности правильной адаптации.
На стадии уточнения (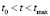 ) радиус обучения определялся экспоненциально убывающей функций (3). При этом пересчет кратчайших расстояний на основе измененной топологии сети показал высокую эффективность для задачи адаптации в окрестности светопроводящих каналов. Пример построения конечно-элементной сетки приведен на рис. 4.
) радиус обучения определялся экспоненциально убывающей функций (3). При этом пересчет кратчайших расстояний на основе измененной топологии сети показал высокую эффективность для задачи адаптации в окрестности светопроводящих каналов. Пример построения конечно-элементной сетки приведен на рис. 4.
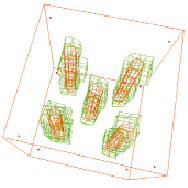
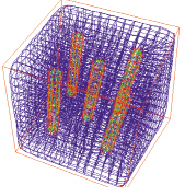
а б
Рис. 4. Результаты применения алгоритма: а) внутренние границы после удаления узлов; б) результат построения сети
Выводы
Разработанный композиционный алгоритм позволяет автоматизировать процесс генерации конечно-элементной сетки пространственной области, характеризующейся наличием узких светопроводящих каналов, длина которых сопоставима с ее диаметром. В новом композиционном алгоритме выделены этапы предварительного уточнения области, уточнения внешней границы, удаления узлов сети и упорядочения. Разработан способ ослабления латеральных связей между узлами, разделенными узким светопроводящим каналом на основе расчета кратчайших расстояний между узлами сети. Вычислительные эксперименты по синтезу конечно-элементной сетки светопроводящего материала подтвердили рекомендации по выбору параметров обучения нейросети на односвязной плоской области. Результаты исследований будут использованы при численном моделировании физических свойств светопроводящих материалов с использованием современных CAE-систем инженерного анализа.
Библиографическая ссылка
Архипов С.В., Дамдинов Б.Б. СИНТЕЗ КОНЕЧНО-ЭЛЕМЕНТНОЙ СЕТКИ СВЕТОПРОВОДЯЩЕГО МАТЕРИАЛА НЕЙРОСЕТЕВЫМИ МЕТОДАМИ // Фундаментальные исследования. 2017. № 4-2. С. 237-241;URL: https://fundamental-research.ru/ru/article/view?id=41467 (дата обращения: 03.01.2026).



