В настоящее время вейвлеты имеют широкое применение в следующих областях обработки и анализа различных сигналов: сжатие и шумоподавление, анализ речевых сигналов в системах распознавания речи [5], психологические и медицинские исследования, такие как оценка состояния эмоциональной напряженности, основанная на многоуровневом вейвлет-анализе речевого сигнала [2], акустографическое исследование тонов и шумов сердца, звуков легких, дыхательных шумов и т.д. Различные подходы в шумоподавлении используются для распознавания звуковых сигналов, при анализе изображений, в системах передачи цифровых данных и т.д.
SNR (signal-to-noise ratio, отношение сигнал/шум) – безразмерная величина, характеризующая отношение мощности полезного сигнала к мощности шума. Она основана на аддитивной модели шума, в которой квантованный сигнал xq[n] представляет собой суперпозицию неквантованного, неискаженного сигнала x[n] и добавочной ошибки квантования e[n]. Отношение мощностей сигналов определяет SNR. SNR обычно приводится в логарифмической шкале в децибелах (дБ) для того, чтобы охватить широкий диапазон потенциальных значений SNR и рассмотреть логарифмическое восприятие людей:
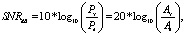
где Px, Pe – средние мощности соответствующих сигналов, а Ax, Ae – среднее значение амплитуд. SNR часто называют отношение сигнал/шум квантования SQNR (signal to quantization-noise ratio).
По характеру источника возникновения различают механический, электрический, акустический, электромагнитный, механический и прочие шумы. Также существует дополнительная классификация шумов, основанная на частотных и спектральных характеристиках: белый шум, белый шум с ограниченной полосой пропускания, узкополосный шум, цветной шум, импульсивный шум, временные шумовые импульсы и т.д.
Белый шум определяется как некоррелированный случайный шумовой процесс, энергия которого одинакова на всех частотах. Случайный шум имеет одинаковую энергию на всех частотах в диапазоне ∞, поэтому обязательно должна присутствовать бесконечная энергия, вследствие чего данный вид шума является чисто теоретическим понятием [7]. Однако шумовой процесс с ограниченной полосой пропускания и равномерным спектром покрывает весь частотный диапазон ограниченной системы, поэтому его практически можно отнести к белому шуму. В классической теории связи предполагается, что шум является стационарным аддитивным белым гауссовым шумом.
На речевой сигнал добавляется аддитивный белый гауссовский шум, осуществляется процесс шумоподавления, основанный на вейвлет-анализе, с применением различных семейств вейвлетов. Затем осуществляется анализ полученных результатов.
Рассмотрим предложенную модель и результаты исследования.
Характеристики используемых вейвлетов
Вейвлеты имеют две характеристики – масштабирующий коэффициент и смещение, взаимосвязь между которыми примерно соответствует операции масштабирования. При малых масштабах используются сжатые вейвлеты, они соответствуют быстро меняющимся сигналам (высокочастотным). При больших масштабах вейвлеты растягиваются, они соответствуют медленно меняющимся сигналам (низкочастотным). В отличие от других инструментов преобразований (преобразование Фурье и др.), используемых в обработке сигналов, вейвлеты позволяют анализировать сигналы одновременно в частотной и временной областях.
Вейвлет-преобразования делятся на две группы: дискретное вейвлет-преобразование (ДВП) и непрерывное вейвлет-преобразование (НВП). Оба преобразования являются непрерывными во времени (аналоговыми), и с их помощью можно представлять аналоговые сигналы. НПВ позволяет использовать все возможные коэффициенты масштабирования и смещения, в то время как в ДВП используется их определенное подмножество (сетка). Когда коэффициенты вейвлет-функций представлены как Z-преобразование, количество нулей на π соответствует количеству нулевых моментов.
Наличие р нулевых моментов означает, что коэффициенты многочлена p-го порядка будут нулевыми. То есть любой полиномиальный сигнал до р – 1 порядка включительно будет полностью представлен в масштабированном пространстве. Теоретически большое количество нулевых моментов означает, что функция масштабирования может точно представить большее количество сложных сигналов. Количество нулевых моментов р также называется точностью вейвлета.
Вейвлеты Дебоши представляют собой семейство ортогональных вейвлетов, определяющих дискретное вейвлет-преобразование. Они характеризуются максимальным числом нулевых моментов для некоторого заданного носителя. В каждом типе вейвлета этого класса масштабирующая функция (отцовский вейвлет) осуществляет кратномасштабный анализ.
В общем случае вейвлеты Дебоши выбираются таким образом, чтобы число А нулевых моментов было максимальным (это не означает лучшая гладкость) для заданной ширины носителя N = 2A [8]. Среди 2A–1 возможных вариантов предпочтительным является тот вейвлет, чей масштабирующий фильтр имеет крайнюю фазу.
Вейвлеты Койфлеты – дискретные вейвлеты, имеющие масштабирующие функции с нулевыми моментами. Данные вейвлеты являются почти симметричными, их вейвлетные функции имеют N/3 нулевых момента, а масштабирующие – N/3–1.
Вейвлеты Дебоши девятого и десятого порядков (db9 и db10) являются асимметричными [3], ортогональными и биортогональными, вейвлет Койфлет пятого порядка (coif5) является почти симметричным, ортогональным и биортогональным.
Фильтрация: приближения и детализации
Для большинства сигналов их низкочастотная составляющая является наиболее важной частью потому, что с ее помощью можно идентифицировать сигнал [6]. Высокочастотная составляющая в свою очередь несет в себе очертания сигнала. Если в человеческом голосе удалить высокочастотную составляющую, то голос поменяется, но слова останутся распознаваемыми. Однако если удалить большое количество низкочастотных составляющих сигнала речь станет нераспознаваемой. В вейвлет-анализе приближения исследуются на больших масштабах, низкочастотные составляющие и детализации – на маленьких [4]. На рис. 1 показано разложение сигнала при помощи вейвлет-анализа, где ФНЧ – фильтр низких частот, ФВЧ – фильтр высоких частот, А – приближение, D – детализация.
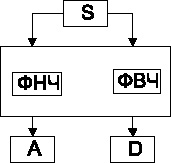
Рис. 1. Разложение сигнала при помощи вейвлет-анализа
Процесс разложения может итеративно повторяться, причем последовательные разложения раскладываются таким образом, что один сигнал дробится на множество сигналов более низкого разрешения.
Так как процесс разложения является итеративным, в теории его можно продолжать до бесконечности. На практике процесс можно продолжать до тех пор, пока отдельные детализации состоят из одного образца или пикселя.
Трешолдинг
Трешолдинг (пороговая обработка данных) – техника исследования сигналов, содержащих шум, осуществляющая декомпозицию исходного сигнала в вейвлет-спектр, который в дальнейшем подвергается обработке. Вейвлет-спектр – функция, содержащая два аргумента (время и масштаб). Результатом дискретного вейвлет-преобразования является N последовательностей, в которых номер – координата масштаба, а номер элемента в последовательности – временная координата. Для исходных сигналов большой длины N является величиной маленького размера (ограничена log2M, где M – число отсчетов исследуемого сигнала). В дискретном вейвлет-спектре (ДВС) последовательности могут иметь большую величину (порядка M2), что позволяет их обрабатывать независимо друг от друга. Жесткий трешолдинг (совмещенный с адаптивным алгоритмом выбора порога) позволяет удалять шум при отсутствии вспомогательной информации о сигнале.
Процесс шумоподавления
Вначале для зашумленного сигнала осуществляется вейвлет-пакетное преобразование, затем для дерева вейвлет-декомпозиции осуществляется пороговая обработка (трешолдинг) данных.
Реализация в системе Matlab:
load mtlb;
x = mtlb;
y = awgn(x,10,’measured’);
wname = ‘coif5’;
lev = 3;
tree = wpdec(y,lev,wname);
[thr,sorh,keepapp,crit] = ddencmp(‘den’,’wp’,y);
xd = wpdencmp(tree,’s’,’nobest’,thr,keepapp);
D=crosscorr(x,xd);
z=-20:1:20;
figure(1)
subplot(311)
plot(x)
title(‘original signal’);
subplot(312)
plot(y,’k’)
title(‘signal with noise’);
subplot(313)
plot(xd,’g’)
xlabel(‘time’)
ylabel(‘Amplitude’)
title(‘signal denoise’);
figure(2)
plot(z,D);
val = D(ceil(size(D,1)/2));
text(1,val, [‘=’,num2str(val)]);
title(wname);
legend(strcat(‘Correlation @ ‘,wname));
Анализ результатов
В качестве метрики анализа шумоподавления используется взаимная корреляционная функция. Взаимная корреляционная функция – функция, оценивающая степень корреляции двух последовательностей [1]. Для непрерывных последовательностей определяется по формуле
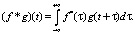
Для дискретных:
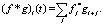
Используемые семейства вейвлетов показали следующие результаты средних значений взаимной корреляционной функции в точке 0:
- вейвлет Дебоши десятого порядка – 0,79325;
- вейвлет Дебоши девятого порядка – 0,78812;
- симлета четвертого порядка – 0,78901;
? койфлета пятого порядка – 0,78759.
Наибольшее значение имели вейвлет Дебоши десятого порядка и койфлет пятого порядка (рис. 2–4).
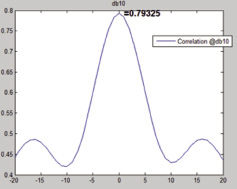
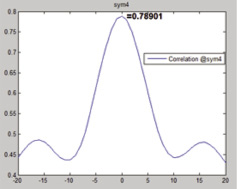
Рис. 2. Графики функций взаимной корреляции для шумоподавления с использованием вейвлета Дебоши (значение в точке ноль – 0,79325) десятого порядка и симлета четвертого порядка (значение в точке ноль – 0,78901)
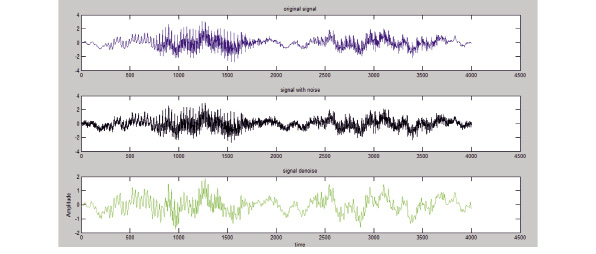
Рис. 3. Шумоподавление с использованием вейвлета Дебоши десятого порядка
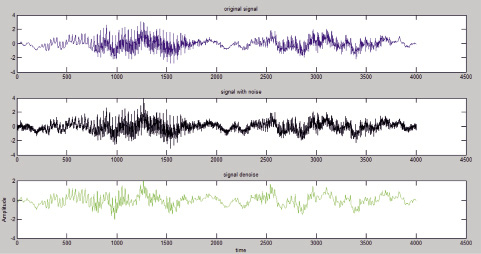
Рис. 4. Шумоподавление с использованием симлета четвертого порядка
Заключение
В данной статье была описана практическая реализация шумоподавления в речевых сигналах на основе вейвлет-анализа. Проведено сравнение использования вейвлетов различных семейств: вейвлеты Дебоши девятого и десятого порядков, симлет четвертого порядка и вейвлет койфлет пятого порядка. Значение взаимной корреляции в точке 0 у всех семейств порядка 0,8, графики функций имеют правильную форму, с учетом того, что исходный сигнал содержал некоторую шумовую составляющую, а вдобавок к ней был добавлен белый гауссов аддитивный шум, результаты шумоподавления являются достаточно высокими.
Библиографическая ссылка
Белов Ю.С., Нифонтов С.В., Азаренко К.А. ПРИМЕНЕНИЕ ВЕЙВЛЕТ-ФИЛЬТРАЦИИ ДЛЯ ШУМОПОДАВЛЕНИЯ В РЕЧЕВЫХ СИГНАЛАХ // Фундаментальные исследования. 2017. № 4-1. С. 29-33;URL: https://fundamental-research.ru/ru/article/view?id=41430 (дата обращения: 21.02.2026).



