В настоящее время получили широкое развитие современные методы и алгоритмы анализа радиотехнических сигналов и их производных на фоне шумов регистрации. Такие достаточно сложные задачи возникают при математическом и вычислительном моделировании объектов, описываемых дифференциальными уравнениями различного порядка, а также при обработке изображений в задаче выделения контуров. Без эффективного решения задач такого рода невозможно вести речь о создании информационных систем обработки радиосигналов и телевизионных изображений.
Обеспечение необходимых требований, предъявляемых к современным системам технического зрения при решении задач высокой сложности, сопряженными с высокой изменчивостью рабочей сцены, разнородностью объектов, помехами и др., напрямую связано с задачей повышения эффективности процесса цифровой обработки сигнала, регистрируемого датчиками систем технического зрения. В частности, одной из проблем применения в априорно неизвестных условиях наблюдения является наличие шума, обусловленного различными факторами, такими как дефекты системы регистрации, влияние окружающей среды и т.п.
Стремительное развитие микропроцессорной техники в последнее время создаёт условия для появления новых применений и расширения и без того широкого спектра задач, решаемых с помощью систем технического зрения, что свидетельствует об актуальности исследований в области повышения эффективности и устойчивости методов и алгоритмов цифровой обработки сигналов. Актуальность проведения исследований существующих и создания новых методов цифрового дифференцирования телевизионных сигналов не вызывает сомнений [1–3, 5].
Цель работы: строгое математическое обоснование и разработка новых высокоточных методов дифференцирования сигналов, регистрируемых на фоне шума с использованием математического аппарата сплайн-аппроксимации.
Кривые, встречающиеся в практических задачах, обычно имеют довольно сложную форму, не позволяющую выполнению аналитического задания в целом при помощи элементарных функций. Поэтому их собирают из сравнительно простых гладких фрагментов – отрезков (кривых), каждый из которых может быть вполне удовлетворительно описан при помощи элементарных функций. При этом желательно чтобы гладкие функции, которые используются для построения частичных отрезков, были бы многочленами одинаковой степени. А чтобы получающаяся в результате кривая оказалась достаточно гладкой, необходимо обращать внимание на места стыковки кусочных фрагментов [8–10].
Для гладкого изменения касательной вдоль всей составной кривой достаточно описывать стыкуемые кривые при помощи многочленов третьей степени. Коэффициенты таких многочленов всегда можно подобрать так, чтобы кривизна соответствующей составной кривой была непрерывной [1, 4]. И здесь вполне естественно использовать кубические сплайны, описываемые при помощи многочленов третьей степени. Существующие методы предварительной обработки сигналов связаны в основном с использованием цифровых фильтров. В тех случаях, когда в процессе обработки подавляется высокочастотная составляющая, говорят о сглаживании. Весьма популярными стали сплайновые методы сглаживания, что обусловлено естественностью постановки задачи сглаживания для сплайнов в силу их вариационных свойств. Хорошие дифференциальные и аппроксимационные свойства делают аппарат сплайнов универсальным средством обработки информации [11].
Применение сглаживающих сплайнов наиболее эффективно в случаях, когда погрешность результатов измерений велика. Если сглаживать функцию кубическим сплайном и затем дифференцировать сплайн-функцию, то полученное в результате выражение будет эквивалентно сглаживанию параболическим сплайном. Применение сплайн-аппроксимации позволяет значительно сократить время первичной обработки измерений, даже при работе с большими массивами данных [5–7].
Рассмотрим область φ = [a; b], на которой определена функция Fu(x), где N – число шагов разбиения сигнала. Введем в области φ множество узлов с равным шагом разбиения h:
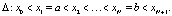 (1)
(1)
Получим аналитическое выражение для сплайн – аппроксимации сигнала, в виде системы сглаживающих кубических нормализованных В-сплайнов дефекта 1 [5, 6]:
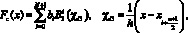 (2)
(2)
где bi – коэффициенты сплайна; 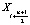 – координаты средины носителя В-сплайна; n – степень сплайна.
– координаты средины носителя В-сплайна; n – степень сплайна.
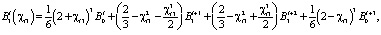 (3)
(3)
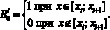 (4)
(4)
Задачу сглаживания будем решать, минимизируя функционал вида [7, 8]:
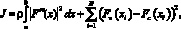 (5)
(5)
где ρ – коэффициент сглаживания; Fu(xi) – значение сглаживаемой функции в узлах сетки; Fc(xi) – значение сплайна в точке xi; 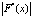 – модуль второй производной сплайна.
– модуль второй производной сплайна.
Рассмотрим участок [xi; xi+1] и осуществим привязку коэффициентов сплайна к средине соответствующего носителя. Тогда для этого участка, с учетом (4), выражение (5) примет вид [6, 7, 9]
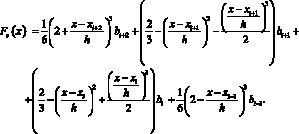 (6)
(6)
Введем нормализованную координату для сплайна, равную 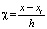 , тогда выражение (6) можно записать в виде
, тогда выражение (6) можно записать в виде
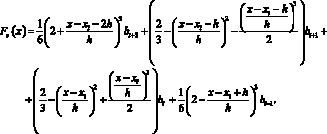 (7)
(7)
После несложных арифметических преобразований, группирования относительно коэффициентов сплайна и подстановки в (6) получим аналитическое выражение для сплайна в виде
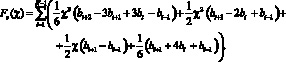 (8)
(8)
Таким образом, функционал запишется в виде:
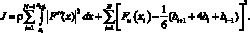 (9)
(9)
Для нахождения коэффициентов сплайна (8), приносящего минимум функционалу (9), вычислим частные производные 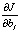 ,
, 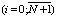 и приравняем их к нулю. В результате этой операции получим систему из N+2 линейных уравнений матричная форма, которых имеет вид [6, 5]
и приравняем их к нулю. В результате этой операции получим систему из N+2 линейных уравнений матричная форма, которых имеет вид [6, 5]
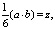 (10)
(10)
где 
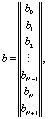
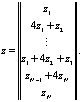
Матрица коэффициентов системы (10) имеет семидиагональный вид и хорошо обусловлена. Решая эту систему одним из известных методов, находим значения искомых коэффициентов. Дифференцируя в аналитическом виде (8), получим выражение для сплайн-аппроксимации производной сигнала:
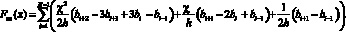 (11)
(11)
Применение на практике данного метода аппроксимации сплайнами дифференцированных сигналов позволяет значительно уменьшить время обработки.
Выводы
Обеспечение необходимых требований, предъявляемых к современным системам технического зрения при решении задач высокой сложности, сопряженными с высокой изменчивостью рабочей сцены, разнородностью объектов, помехами и др., напрямую связано с задачей повышения эффективности процесса цифровой обработки сигнала, регистрируемого датчиками систем технического зрения автономных роботов. В частности, одной из проблем применения в априорно неизвестных условиях наблюдения является наличие шума, обусловленного различными факторами, такими как дефекты системы регистрации, влияние окружающей среды и т.п. Предложенный впервые новый высокоточный метод цифрового дифференцирования сигналов позволяет, не пользуясь стандартными процедурами численного дифференцирования, которые сами по себе являются некорректными с достаточно высокой точностью вычислять как значение самого сигнала, так и значения его производной.
Стремительное развитие микропроцессорной техники в последнее время создаёт условия для появления новых применений и расширения и без того широкого спектра задач, решаемых с помощью систем технического зрения, что свидетельствует об актуальности исследований в области повышения эффективности и устойчивости методов и алгоритмов цифровой обработки сигналов. Используя математический аппарат дифференцирования при помощи сплайнов для обработки результатов измерений, значительным является то, что в численной схеме используется ограниченное число коэффициентов разложения. Применение кубических нормализованных В-сплайнов в задаче аппроксимации дифференцированных сигналов существенно уменьшает время обработки.
Библиографическая ссылка
Безуглов Д.А., Крутов В.А., Швачко О.В. МЕТОД ДИФФЕРЕНЦИРОВАНИЯ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ СПЛАЙН-АППРОКСИМАЦИИ // Фундаментальные исследования. 2017. № 4-1. С. 24-28;URL: https://fundamental-research.ru/ru/article/view?id=41429 (дата обращения: 06.01.2026).



