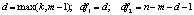Большинство анализируемых экономических данных представляют собой многомерные генеральные совокупности со взаимосвязанными компонентами. Причем связь между компонентами чаще всего не функциональная, а стохастическая. Поэтому представляется логичным использование многомерных методов статистического анализа для их исследования.
Одной из проблем, решаемых математической статистикой, является проблема проверки однородности данных, т.е. принадлежности различных групп данных к одной генеральной совокупности, одномерной или многомерной, с целью их дальнейшего объединения в одну генеральную совокупность и последующей статистической обработки всего массива данных целиком. Если сравниваются две группы данных, то задача сводится к проверке статистической гипотезы о равенстве средних, если групп данных более двух, то к дисперсионному анализу.
В данной статье многомерный дисперсионный анализ (MANOVA) используется для проверки однородности многомерных экономических данных – уровня потребления основных продуктов питания. Прежде чем приступить непосредственно к применению дисперсионного анализа, напомним читателю его основные положения.
Однофакторный одномерный дисперсионный анализ (One-way ANOVA)
В дисперсионном анализе изучается влияние одного или нескольких факторов (независимых категориальных переменных) на результаты наблюдений (значения зависимой переменной X) [11].
Рассмотрим влияние на зависимую переменную Х одного фактора А, принимающего m значений – уровней – 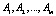 . На i-том уровне фактора имеется выборка
. На i-том уровне фактора имеется выборка 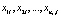 объема ni, i = 1, 2, …,m. В общем случае объемы выборок могут быть неравными. Общее число наблюдений равно n = n1 + n2 + … + nm. Исходные данные обычно представляют в виде таблицы (табл. 1).
объема ni, i = 1, 2, …,m. В общем случае объемы выборок могут быть неравными. Общее число наблюдений равно n = n1 + n2 + … + nm. Исходные данные обычно представляют в виде таблицы (табл. 1).
Таблица 1
Исходные данные для ANOVA
|
A1 (Выборка 1) |
A2 (Выборка 2) |
… |
Am (Выборка m) |
|
|
|
|
… … … … … |
|
|
|
Выборочное среднее |
|
|
… |
|
|
Объем выборки |
n1 |
n2 |
… |
nm |
Предполагается, что все выборки, их еще называют группами, независимы и извлечены из нормально распределенных совокупностей с равными дисперсиями: N(μ1, s2), N(μ2, s2), …, N(μm,s2).. В однофакторном дисперсионном анализе проверяется гипотеза о равенстве математических ожиданий этих генеральных совокупностей: 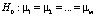 , т.е. о несущественном влиянии фактора А на результаты наблюдений. Альтернативная гипотеза утверждает, что не все mi равны между собой.
, т.е. о несущественном влиянии фактора А на результаты наблюдений. Альтернативная гипотеза утверждает, что не все mi равны между собой.
Для описания результатов наблюдений используется линейная модель:
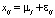 ,
,
где εij – неизвестные одинаково распределенные случайные величины, характеризующие случайную ошибку, вызванную влиянием неконтролируемых факторов.
В качестве статистического критерия принимается F-критерий:
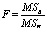 ,
,
в случае справедливости нулевой гипотезы имеющий распределения Фишера F(m – 1, n – m),
где 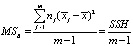 – межгрупповая (факторная) дисперсия (Mean Square between groups),
– межгрупповая (факторная) дисперсия (Mean Square between groups),
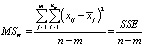 – внутригрупповая (остаточная) дисперсия (Mean Square within groups),
– внутригрупповая (остаточная) дисперсия (Mean Square within groups),
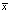 – общая средняя,
– общая средняя,
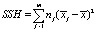 – межгрупповая сумма квадратов отклонений (Hypothesis Sum of Squares),
– межгрупповая сумма квадратов отклонений (Hypothesis Sum of Squares),
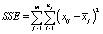 – внутригрупповая сумма квадратов отклонений (Error Sum of Squares).
– внутригрупповая сумма квадратов отклонений (Error Sum of Squares).
MSB и MSW являются статистическими оценками генеральной дисперсии σ2, характеризующими разброс данных между выборками и внутри выборок соответственно. Если математические ожидания mi не равны между собой, то разброс данных внутри групп относительно групповых средних должен быть меньше, чем разброс групповых средних относительно общей средней, и тогда значение F-критерия будет большим. Нулевая гипотеза отвергается, если F > Fкр. На этом основана идея одномерного дисперсионного анализа.
Однофакторный многомерный дисперсионный анализ (One-way MANOVA)
Естественным обобщением ANOVA на многомерный случай является многомерный дисперсионный анализ – MANOVA (Multivariable Analysis of Variances).
В многомерном случае предполагается, что m независимых выборок 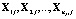 , j = 1,2,…,m, извлечены из k-мерных генеральных совокупностей, имеющих многомерное нормальное распределение с одинаковыми ковариационными матрицами S. Таким образом, изучается влияние одного фактора A – одной независимой категориальной переменной – на k-мерный вектор зависимых переменных
, j = 1,2,…,m, извлечены из k-мерных генеральных совокупностей, имеющих многомерное нормальное распределение с одинаковыми ковариационными матрицами S. Таким образом, изучается влияние одного фактора A – одной независимой категориальной переменной – на k-мерный вектор зависимых переменных 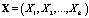 , коррелирующих между собой. Общее число векторов наблюдений равно n = n1 + n2 + … + nm .
, коррелирующих между собой. Общее число векторов наблюдений равно n = n1 + n2 + … + nm .
Исходные данные можно представить в виде таблицы (табл. 2), где 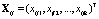 – k-мерные векторы наблюдений, i = 1,2,…,nj, j = 1,2,…,m,
– k-мерные векторы наблюдений, i = 1,2,…,nj, j = 1,2,…,m, 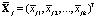 – k-мерные векторы выборочных средних с компонентами
– k-мерные векторы выборочных средних с компонентами 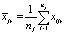 , r = 1, 2,…,k.
, r = 1, 2,…,k.
Таблица 2
Исходные данные для MANOVA
|
A1 (Выборка 1) |
A2 (Выборка 2) |
… |
Am (Выборка m) |
|
|
|
|
… … … … … |
|
|
|
Вектор выборочных средних |
|
|
… |
|
|
Объем выборки |
n1 |
n2 |
… |
nm |
Вектор общих средних имеет вид
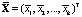 ,
,
где 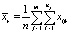 , r = 1, 2,…,k.
, r = 1, 2,…,k.
Результаты наблюдений описываются линейной моделью
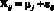 ,
,
или в векторной форме
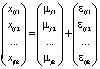 ,
,
где εijr – неизвестные одинаково распределенные случайные величины, характеризующие случайную ошибку, r = 1, 2,…,k.
Нулевая гипотеза в многомерном случае имеет вид
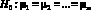 ,
,
где 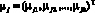 – k-мерные векторы математических ожиданий зависимых переменных, j = 1, 2,…,m, то есть требуется проверить выполнение равенств для соответствующих компонент векторов
– k-мерные векторы математических ожиданий зависимых переменных, j = 1, 2,…,m, то есть требуется проверить выполнение равенств для соответствующих компонент векторов 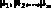 .
.
Важнейшим преимуществом проведения однократной процедуры MANOVA для k-мерного вектора зависимых переменных 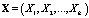 вместо проведения k процедур ANOVA отдельно для каждой из зависимых переменных Xr, r = 1, 2,…,k, является учет корреляции зависимых переменных друг с другом, что позволяет учесть все связи, скрытые в массивах многомерных числовых данных [2]. Кроме того, многомерный дисперсионный анализ является первым этапом на пути к решению проблемы классификации исследуемых объектов, а также предварительным шагом перед проведением процедуры снижения размерности данных путем исключения наименее важных признаков. Еще одним достоинством MANOVA является тот факт, что он менее чувствителен к условию нормальности исходных данных, чем ANOVA. Поэтому его применяют вместо ANOVA еще и для анализа повторных данных, для которых не выполняется условие сферичности.
вместо проведения k процедур ANOVA отдельно для каждой из зависимых переменных Xr, r = 1, 2,…,k, является учет корреляции зависимых переменных друг с другом, что позволяет учесть все связи, скрытые в массивах многомерных числовых данных [2]. Кроме того, многомерный дисперсионный анализ является первым этапом на пути к решению проблемы классификации исследуемых объектов, а также предварительным шагом перед проведением процедуры снижения размерности данных путем исключения наименее важных признаков. Еще одним достоинством MANOVA является тот факт, что он менее чувствителен к условию нормальности исходных данных, чем ANOVA. Поэтому его применяют вместо ANOVA еще и для анализа повторных данных, для которых не выполняется условие сферичности.
В отличие от одномерного случая вместо межгрупповой и внутригрупповой сумм квадратов SSH и SSE рассматриваются их обобщения – межгрупповая и внутригрупповая матрицы H и E (симметричные квадратные матрицы порядка k), определяемые следующим образом [12]:
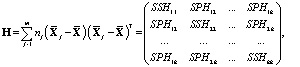
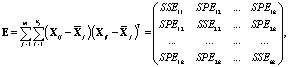
где 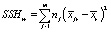 – межгрупповые суммы квадратов (Hypothesis Sums of Squares),
– межгрупповые суммы квадратов (Hypothesis Sums of Squares),
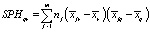 – межгрупповые суммы произведений (Hypothesis Sums of Products),
– межгрупповые суммы произведений (Hypothesis Sums of Products),
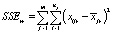 – внутригрупповые суммы квадратов (Error Sums of Squares),
– внутригрупповые суммы квадратов (Error Sums of Squares),
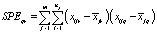 – внутригрупповые суммы произведений (Error Sums of Products),
– внутригрупповые суммы произведений (Error Sums of Products), 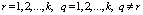 .
.
Для проверки нулевой гипотезы используются четыре статистических критерия [2, 12], приведенных в табл. 3. Все критерии – это скалярные величины, рассчитанные с помощью матриц H и E и основанные на различных подходах к определению критических статистик. Критические значения критериев можно найти в специальных таблицах [12]. В табл. 3 также приведены выражения для критериев через собственные значения 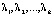 матрицы
матрицы 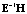 или матрицы
или матрицы 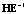 (собственные значения обеих матриц совпадают, но собственные векторы различны!).
(собственные значения обеих матриц совпадают, но собственные векторы различны!).
Таблица 3
Статистические критерии для MANOVA
|
Статистический критерий |
Формула |
Критическая область |
Выражение критерия через собственные значения матрицы |
|
Лямбда Уилкса (Wilks’ Lambda) |
|
|
|
|
След Хотеллинга (Hotelling’s Trace) |
|
|
|
|
След Пиллая (Pillai’s Trace) |
|
|
|
|
Максимальный корень по методу Роя (Roy’s Largest Root) |
где λ1 – наибольшее собственное значение матрицы |
|
|
Данные статистические критерии можно аппроксимировать F-статистикой Фишера со степенями свободы df1, df2 [2, 12]. Соответствующие формулы приведены в табл. 4.
Таблица 4
Аппроксимация критериев F-статистикой
|
Статистический критерий |
Соответствующая аппроксимирующая F-статистика со степенями свободы df1, df2 |
|
Лямбда Уилкса (Wilks’ Lambda) |
где
|
|
След Хотеллинга (Hotelling’s Trace) |
где
|
|
След Пиллая (Pillai’s Trace) |
где
|
|
Максимальный корень по методу Роя (Roy’s Largest Root) |
Ввиду отсутствия удовлетворительной аппроксимации критерия F-статистикой используется ее приблизительная «верхняя граница»:
где
|
Необходимо отметить, что максимальный корень по методу Роя является более мощным критерием по сравнению с тремя другими только в том случае, если векторы средних значений коллинеарны между собой [12]. Это возможно в ситуации, когда наибольшее собственное значение l1 существенно превосходит (в несколько раз) все остальные собственные значения. В остальных случаях его можно не принимать во внимание.
Анализ потребления продуктов питания
Показатели душевого потребления основных продуктов питания входят в число критериев оценки уровня жизни населения в регионе. Неоднородность потребления продуктов в регионах Российской Федерации объясняется различиями в доходах, уровнем развития сельского хозяйства в регионе, степенью обеспеченности региона определенным видом продукта, климатическими особенностями, наконец, исторически сложившимися традициями в питании в конкретном регионе. Например, спрос на мясо и мясопродукты выше в регионах с высокими среднедушевыми доходами; в регионах со средним уровнем доходов и высоким уровнем развития сельхозпроизводства высокий уровень потребления всех продуктов питания обеспечивается более низкими ценами из-за конкуренции сельхозпроизводителей [3] и т.д. Возникают закономерные вопросы: существенны ли различия в потреблении продуктов питания в регионах России и существенно ли меняется потребление с течением времени?
Статистические данные по потреблению основных продуктов питания в регионах Российской Федерации за разные временные промежутки анализировались во многих работах [1, 3, 4, 6–9], в том числе и с применением одномерного дисперсионного анализа [5, 10]. Как правило, в подобных исследованиях регионы (или федеральные округа) сравниваются по уровню потребления друг с другом или с рациональными нормами питания отдельно по каждому из основных продуктов питания, проводится разбиение регионов на кластеры, делаются попытки построить уравнения регрессии и дать прогноз. Мы же попробуем сравнить между собой федеральные округа по уровню потребления совокупности всех основных продуктов одновременно. Представляется, что такой подход является обоснованным в силу существующих взаимосвязей (соотношений) между уровнем потребления разных видов продуктов: недостаточное потребление одного вида продукта компенсируется избыточным потреблением другого (например, мясо – картофель), или увеличенное потребление одного влечет увеличенное потребление другого сопутствующего продукта (например, ягоды – сахар).
В статье рассматривается анализ потребления основных продуктов питания в различных округах Российской Федерации по данным Росстата за 2014 год. Изучается влияние территориального фактора – федерального округа – на восьмимерный вектор показателей потребления
X = (X1, X2,…, X8),
где X1 – душевое потребление мяса и мясопродуктов (кг за год),
X2 – душевое потребление молока и молочных продуктов (кг за год),
X3 – душевое потребление яиц (шт за год),
X4 – душевое потребление сахара (кг за год),
X5 – душевое потребление картофеля (кг за год),
X6 – душевое потребление овощей и бахчевых культур (кг за год),
X7 – душевое потребление растительного масла (кг за год),
X8 – душевое потребление хлебных продуктов (кг за год).
Исходные данные частично представлены в табл. 5.
Таблица 5
Исходные данные (по данным Росстата)
|
Продукты питания |
|||||||||
|
Округ |
Регион |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
ЦФО |
Белгородская область |
97 |
261 |
318 |
47 |
119 |
110 |
13,8 |
139 |
|
ЦФО |
Брянская область |
64 |
208 |
230 |
34 |
155 |
100 |
11,2 |
114 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
ДФО |
Чукотский авт. округ |
51 |
109 |
147 |
34 |
59 |
26 |
17,8 |
61 |
Таким образом, в переводе на язык математической статистики, изучается влияние территориального фактора, имеющего восемь уровней (по числу федеральных округов), на вектор показателей потребления X = (X1, X2,…, X8). Число наблюдений (объемы выборок 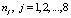 ) на каждом уровне фактора различно, так как в каждом федеральном округе разное число регионов.
) на каждом уровне фактора различно, так как в каждом федеральном округе разное число регионов.
Перечисленные продукты питания хотя и слабо, но коррелируют между собой. Корреляционная матрица по данным за 2014 год выглядит следующим образом (табл. 6).
Таблица 6
Корреляционная матрица
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
|
X1 |
1 |
0,342 |
0,224 |
0,268 |
– 0,004 |
– 0,028 |
0,140 |
0,147 |
|
X2 |
0,342 |
1 |
0,335 |
0,104 |
0,020 |
0,165 |
0,085 |
0,222 |
|
X3 |
0,224 |
0,335 |
1 |
0,293 |
0,092 |
0,230 |
0,241 |
0,126 |
|
X4 |
0,268 |
0,104 |
0,293 |
1 |
– 0,008 |
0,244 |
0,238 |
0,371 |
|
X5 |
– 0,004 |
0,020 |
0,092 |
– 0,008 |
1 |
0,171 |
– 0,074 |
0,333 |
|
X6 |
– 0,028 |
0,165 |
0,230 |
0,244 |
0,171 |
1 |
0,043 |
0,218 |
|
X7 |
0,140 |
0,085 |
0,241 |
0,238 |
– 0,074 |
0,043 |
1 |
– 0,025 |
|
X8 |
0,147 |
0,222 |
0,126 |
0,371 |
0,333 |
0,218 |
– 0,025 |
1 |
Несмотря на то, что метод MANOVA не очень чувствителен к требованию многомерной нормальности, проверим, нет ли очевидных свидетельств того, что распределение рассматриваемой генеральной совокупности существенно отличается от нормального. Для этого рекомендуется [12], во-первых, проверить на нормальность компоненты вектора X = (X1, X2,…, X8), во-вторых, визуально проанализировать диаграммы рассеяния для всех возможных пар компонент вектора X. Если облако рассеяния для какой-то пары переменных отличается от эллиптического, то есть основание сомневаться в нормальной распределенности генеральной совокупности.
Каждая из рассматриваемых переменных X1, X2,…, X8, взятая по отдельности, имеет распределение, близкое к нормальному, что подтверждается наблюдаемыми частотами распределения каждой переменной, приведенными в табл. 7.
Таблица 7
Наблюдаемые частоты
|
Переменные |
||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
|
Номер интервала |
Частоты |
|||||||
|
1 |
3 |
1 |
1 |
6 |
3 |
2 |
7 |
1 |
|
2 |
8 |
4 |
4 |
8 |
6 |
3 |
13 |
0 |
|
3 |
18 |
14 |
7 |
17 |
17 |
36 |
24 |
6 |
|
4 |
26 |
19 |
14 |
20 |
25 |
28 |
19 |
20 |
|
5 |
17 |
22 |
25 |
15 |
15 |
6 |
9 |
30 |
|
6 |
5 |
14 |
17 |
7 |
7 |
4 |
4 |
18 |
|
7 |
1 |
4 |
11 |
4 |
4 |
0 |
2 |
3 |
|
8 |
2 |
2 |
1 |
3 |
3 |
1 |
2 |
2 |
Диаграммы рассеяния для рассматриваемых переменных – показателей потребления – похожи на показанную на рисунке диаграмму для переменных X1 и X2. Как видно, облако рассеяния имеет форму, близкую к эллиптической. Таким образом, можно принять, что выборка извлечена из многомерной генеральной совокупности, имеющей распределение, близкое к нормальному.
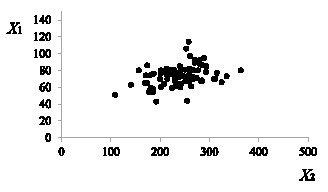
Диаграмма рассеяния переменных X1 и X2
Одним из условий применимости многомерного дисперсионного анализа является равенство ковариационных матриц рассматриваемых групп данных, что проверяется многомерным критерием М-Бокса. В нашем случае данный критерий невозможно применить ко всей совокупности данных, так как число наблюдений в некоторых выборках меньше, чем размерность вектора X, а именно: в Юго-Восточном, Северо-Кавказском и Уральском федеральных округах число регионов равно 6, 7 и 4 соответственно, что меньше, чем число основных продуктов питания.
Применим метод MANOVA к статистическим данным. Проведенные расчеты подтверждают существенность влияния территориального фактора на потребление всех продуктов питания в совокупности. Значения статистических критериев, соответствующая аппроксимирующая F-статистика и ее p-значение даны в табл. 8.
Таблица 8
Результаты расчетов
|
Статистический критерий |
Значение критерия |
Значение аппроксимирующей F-статистики |
p-значение F-статистики |
|
Лямбда Уилкса |
0,116 |
3,114 |
8,05×10-11 |
|
След Хотеллинга |
2,783 |
3,145 |
1,64×10-11 |
|
След Пиллая |
1,716 |
2,883 |
4,03×10-10 |
|
Максимальный корень по методу Роя |
0,939 |
8,333 |
< 0,001 |
Так как для всех четырех критериев p-значение существенно меньше 0,05, то гипотеза о несущественности влияния территориального фактора на уровень потребления продуктов питания отвергается. Таким образом, территориальный фактор оказывает значимое влияние на потребление всей совокупности продуктов. Это означает, что рассматриваемые данные по разным федеральным округам нельзя объединять в одну многомерную генеральную совокупность, следовательно, нельзя их использовать для построения уравнения множественной регрессии, а также сомнительно, что можно применять к ним метод главных компонент.
Если в рамках многомерного дисперсионного анализа гипотеза о несущественности влияния фактора отвергается, то рекомендуется провести k процедур однофакторного дисперсионного анализа, чтобы проанализировать, какие из зависимых переменных вносят наиболее существенный вклад в неоднородность данных. В табл. 9 даны результаты проверки гипотезы о влиянии территориального фактора на уровень потребления каждого из продуктов питания, взятых по отдельности, проведенной с помощью однофакторного дисперсионного анализа по данным за 2014 год.
Таблица 9
Результаты ANOVA для компонент вектора Х
|
Зависимые переменные (продукты питания) |
||||||||
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
|
|
Значение F-критерия |
1,679 |
4,538 |
2,213 |
2,601 |
2,511 |
4,474 |
0,5685 |
1,7134 |
|
p-значение критерия |
0,1278 |
0,0003 |
0,0429 |
0,0189 |
0,0229 |
0,0004 |
0,7791 |
0,1191 |
Полученные результаты свидетельствуют о том, что территориальный фактор не оказывает влияние на потребление трех продуктов питания (мясопродукты, растительное масло и хлебопродукты) при уровне значимости 0,05. Потребление остальных основных продуктов питания существенно различается по федеральным округам.
Если рассмотреть вектор потребления X, включающий только три продукта: мясопродукты, растительное масло и хлебопродукты, и применить многомерный дисперсионный анализ для проверки значимости влияния территориального фактора, то результаты будут следующими (табл. 10).
Таблица 10
Результаты расчетов для трехмерного вектора Х
|
Статистический критерий |
Значение критерия |
Значение аппроксимирующей F-статистики |
p-значение F-статистики |
|
Лямбда Уилкса |
0,669 |
1,439 |
0,103 |
|
След Хотеллинга |
0,444 |
1,451 |
0,098 |
|
След Пиллая |
0,365 |
1,424 |
0,109 |
|
Максимальный корень по методу Роя |
0,294 |
3,028 |
0,008 |
Так как p-значение первых трех критериев превышает 0,05, то гипотезу об отсутствии влияния территориального фактора на потребление данных трех продуктов питания можно принять.
Применение MANOVA к повторным данным
Воспользуемся методом многомерного дисперсионного анализа для выяснения, существенно ли влияет территориальный фактор на изменение потребления продуктов с течением времени. Для этого используем статистические данные Росстата за 2004–2014 годы с шагом 2 года по каждому из основных продуктов питания по отдельности. Фрагмент массива исходных данных по переменной X1 (мясо и мясопродукты) представлен в табл. 11.
Таблица 11
Исходные повторные данные для переменной Х1
|
Душевое потребление мяса и мясопродуктов (кг в год) |
|||||||
|
Округ |
Регион |
2004 |
2006 |
2008 |
2010 |
2012 |
2014 |
|
ЦФО |
Белгородская область |
66 |
80 |
88 |
92 |
97 |
97 |
|
ЦФО |
Брянская область |
58 |
60 |
60 |
61 |
62 |
64 |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
ДФО |
Чукотский авт. округ |
37 |
40 |
50 |
53 |
51 |
51 |
Таблица 12
Преобразованные данные
|
Прирост душевого потребления мяса и мясопродуктов (кг за 2 года) |
||||||
|
Округ |
Регион |
2004–2006 |
2006–2008 |
2008–2010 |
2010–2012 |
2012–2014 |
|
ЦФО |
Белгородская область |
14 |
8 |
4 |
5 |
0 |
|
ЦФО |
Брянская область |
2 |
0 |
1 |
1 |
2 |
|
… |
… |
… |
… |
… |
… |
… |
|
ДФО |
Чукотский авт. округ |
3 |
10 |
3 |
– 2 |
0 |
Таблица 13
Результаты расчетов для повторных данных
|
Статистические критерии |
|||||
|
Продукт |
L |
|
V |
q |
|
|
Мясные продукты |
Значение критерия |
0,597 |
0,564 |
0,475 |
0,287 |
|
F-статистика |
1,060 |
1,054 |
1,064 |
2,907 |
|
|
p-значение |
0,383 |
0,390 |
0,376 |
0,010 |
|
|
Молочные продукты |
Значение критерия |
0,423 |
0,992 |
0,753 |
0,464 |
|
F-статистика |
1,842 |
1,853 |
1,799 |
4,710 |
|
|
p-значение |
0,004 |
0,003 |
0,005 |
< 0,001 |
|
|
Яйца |
Значение критерия |
0,493 |
0,821 |
0,617 |
0,479 |
|
F-статистика |
1,488 |
1,534 |
1,429 |
4,862 |
|
|
p-значение |
0,043 |
0,031 |
0,059 |
< 0,001 |
|
|
Сахар |
Значение критерия |
0,725 |
0,342 |
0,304 |
0,176 |
|
F-статистика |
0,647 |
0,640 |
0,656 |
1,783 |
|
|
p-значение |
0,940 |
0,945 |
0,935 |
0,104 |
|
|
Картофель |
Значение критерия |
0,355 |
1,337 |
0,834 |
0,926 |
|
F-статистика |
2,268 |
2,498 |
2,032 |
9,397 |
|
|
p-значение |
< 0,001 |
< 0,001 |
0,001 |
< 0,001 |
|
|
Овощи и бахчевые |
Значение критерия |
0,364 |
1,203 |
0,865 |
0,605 |
|
F-статистика |
2,208 |
2,249 |
2,121 |
6,135 |
|
|
p-значение |
< 0,001 |
< 0,001 |
< 0,001 |
< 0,001 |
|
|
Растительное масло |
Значение критерия |
0,508 |
0,778 |
0,598 |
0,455 |
|
F-статистика |
1,421 |
1,454 |
1,377 |
4,618 |
|
|
p-значение |
0,065 |
0,052 |
0,081 |
0,000 |
|
|
Хлебные продукты |
Значение критерия |
0,441 |
0,944 |
0,719 |
0,475 |
|
F-статистика |
1,747 |
1,763 |
1,703 |
4,819 |
|
|
p-значение |
0,008 |
0,006 |
0,009 |
< 0,001 |
|
Преобразуем исходные данные: вместо душевого потребления рассмотрим двухгодичный прирост душевого потребления (табл. 12).
К преобразованным данным для всех восьми продуктов питания применим многомерный дисперсионный анализ. Результаты расчетов – значения критериев, аппроксимирующая F-статистика и ее p-значения – представлены в табл. 13.
Таким образом, на протяжении рассматриваемого периода времени территориальный фактор не оказывал существенного влияния на изменение уровня потребления мясных продуктов, сахара и растительного масла и оказывал весомое влияние на изменение потребления яиц, молочных продуктов, картофеля, овощей и хлебных продуктов. То есть можно считать, что изменение потребления мясных продуктов, сахара и растительного масла в течение 10-летнего периода в 2004–2014 годах было однородным на всей территории страны, а уровень потребления остальных продуктов изменялся по-разному в различных федеральных округах. Отметим, что характер изменения уровня потребления с течением времени в данной статье не рассматривается.
Заключение
Группы экономических многомерных данных перед их объединением в одну многомерную совокупность следует проверять на однородность с помощью многомерного дисперсионного анализа. Такая проверка была проведена для статистических данных об уровне потребления основных продуктов питания в регионах Российской Федерации, объединенных в группы по территориальному признаку (федеральные округа).
С помощью многомерного дисперсионного анализа удалось выяснить, что уровень потребления основных продуктов питания существенно различается в различных федеральных округах, поэтому рассматриваемые группы данных нельзя объединять в одну многомерную генеральную совокупность. Если же рассматривать совокупность продуктов, включающую только мясные продукты, хлебные продукты и растительное масло, то тогда потребление можно считать однородным.
Также оказалось, что изменение уровня потребления мясных продуктов, сахара и растительного масла с течением времени однородно по всей территории страны, для других продуктов питания это изменение неоднородно.
Полученные выводы можно использовать в качестве предварительной информации, предшествующей дальнейшему применению многомерных статистических методов для анализа рассматриваемых данных.
Библиографическая ссылка
Макжанова Я.В., Швед Е.В. АНАЛИЗ ПОТРЕБЛЕНИЯ ПРОДУКТОВ ПИТАНИЯ С ИСПОЛЬЗОВАНИЕМ МЕТОДА МНОГОМЕРНОГО ДИСПЕРСИОННОГО АНАЛИЗА (MANOVA) // Фундаментальные исследования. 2017. № 3. С. 149-159;URL: https://fundamental-research.ru/ru/article/view?id=41411 (дата обращения: 20.02.2026).




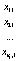
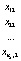
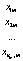
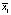
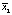
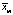
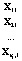
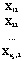
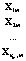
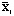
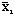
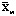
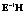
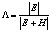
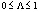
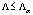
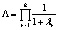
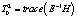
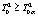
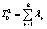
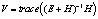
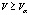
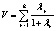
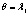 или
или 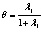 ,
,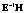
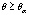
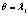 или
или 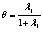
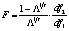 ,
,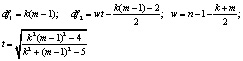
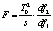 ,
,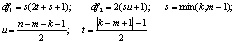
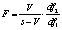 ,
,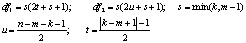
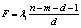 ,
,