Качество электрической энергии является составляющей электромагнитной совместимости и определяется совокупностью характеристик. Снижение качества электрической энергии приводит к причинению вреда электрооборудованию, повышает энергоемкость технологических процессов и воздействует на здоровье людей. Для предотвращения таких последствий необходимо проведение методических, технических и организационных мероприятий. Методические мероприятия включают в себя снижение уровня кондуктивных помех, вносимых электрооборудованием потребителя электроэнергии в систему электроснабжения предприятия и электрические сети энергосистем.
Колебания напряжения являются одним из показателей качества электрической энергии. Они вызываются потребителями электроэнергии, имеющими электрическую нагрузку резкопеременного характера. Уровень допустимых кондуктивных помех нормировался раньше ГОСТ 13109-87, а затем ГОСТ 13109-97. В этих стандартах колебания напряжения характеризовались двумя показателями: размахом изменения напряжения и дозой колебаний (дозой фликера). В 2015 году в действие введен новый стандарт ГОСТ 32144-2013, в котором колебания напряжения характеризуются только одним показателем – дозой фликера.
Рассчитать размах изменения напряжения проще, чем дозу фликера. В связи с этим до последнего времени наибольшее развитие получили методики расчета размахов напряжения электрической сети, питающей различные потребители с резкопеременной нагрузкой [1, 9]. Аналитические методы расчета дозы фликера также предлагались рядом авторов [5, 7], но широкого распространения в практике проектирования они не получили. В настоящее время развитие известных и разработка новых методов расчета дозы фликера в связи с вводом в действие ГОСТ 32144-2013 стали актуальны. Исследования в этом направлении проводятся рядом авторов, например [8].
Ниже описывается предлагаемая авторами методика расчета дозы фликера, возникающего в электрических сетях, питающих асинхронные электродвигатели при стохастическом характере изменения резкопеременных электрических нагрузок. Методика разработана на примере фанерного производства.
Расчет дозы фликера включает в себя выполнение следующих этапов работы, представленных на рис. 1.
Для выполнения первого этапа проектировщику необходимо иметь математические модели электрических нагрузок электроприводов с резкопеременной нагрузкой. Для создания таких моделей исследованы электрические нагрузки электроприводов фанерного производства, работающих в повторно-кратковременном режиме. Результаты исследований показали, что электрические нагрузки основного производства изменяются случайным образом и имеют резкопеременный характер. Графики нагрузок имеют точки экстремума (максимальные и минимальные значения), изменение нагрузок происходит с большой частотой [6]. Выбросы нагрузки электропривода имеют случайную амплитуду и случайную продолжительность. Графики нагрузок активной P(t) и реактивной Q(t) мощностей исследуемых потоков можно классифицировать как периодические нестационарные потоки.
Отсутствие стационарности существенно затрудняет исследование и дальнейшее использование этих графиков. Поэтому авторы статьи предлагают рассматривать эти графики как импульсные случайные процессы со случайными амплитудами, временем цикла и продолжительностью включения. Как показано в [3, 10 ,11], такие процессы являются стационарными, ординарными.
Нами предложено рассматривать графики нагрузок в виде точек экстремумов соответствующих графиков активной и реактивной мощностей, соединенных прямыми линиями. Для расчета дозы фликера необходимо знать численные значения точек экстремумов этих графиков. В связи с этим предлагается описывать графики активной P(t) и реактивной Q(t) мощностей решетчатыми моделями, интерполируемыми сплайн-функциями первой степени.
Например, для графика активной мощности сплайн-функция имеет вид
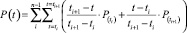 , (1)
, (1)
где n – число циклов, измеренных в результате опыта;
ti – момент появления i-го экстремума;
ti+1 – момент появления (i +1)-го экстремума;
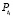 ,
, 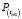 – значение нагрузки в точке экстремума в момент времени ti и ti+1 соответственно.
– значение нагрузки в точке экстремума в момент времени ti и ti+1 соответственно.
При анализе электромагнитной совместимости электродвигателей с питающей их сетью нет необходимости знать законы распределения их электрических нагрузок. Для решения этой задачи достаточно знать их основные числовые характеристики – математические ожидания и дисперсию или среднее квадратическое отклонение.
Математические ожидания и средние квадратические отклонения графиков электрических нагрузок также предлагается описывать решетчатыми моделями интерполированными сплайн-функциями первой степени.
В качестве примера на рис. 2 и 3 представлены полигоны математического ожидания M[P] и среднего квадратического отклонения σ[P] активной мощности главного привода механизма электроприемника барабанной рубильной машины «Дробилка шпона» фанерного производства. Значения по оси ординат даны в процентах от среднего значения активной мощности в период работы рассматриваемого механизма.

Рис. 1. Этапы расчета дозы фликера
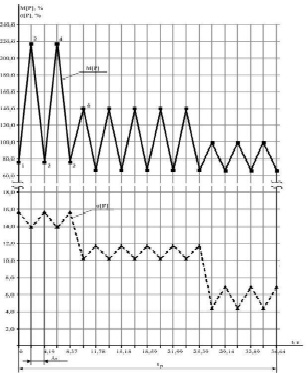
Рис. 2. Полигоны математического ожидания и среднего квадратического отклонения активной мощности рабочего цикла нагрузочной диаграммы электроприемника барабанной рубильной машины «Дробилка шпона» фанерного производства
Напряжения сети в узлах электрической сети, в какой-либо момент времени t = ti, определяют по известному выражению
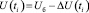 , (2)
, (2)
где
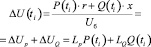 , (3)
, (3)
где Uб – напряжение на источнике питания, В,
r, x – сопротивления электрической сети, Ом,
LP, LQ – линейные операторы активной и реактивной мощностей.
Таким образом, случайные функции P(t) и Q(t) связаны с потерей напряжения ΔU(ti) линейными операторами LP и LQ, и напряжение U(ti), также является случайным процессом, который предлагается описывать решетчатой моделью. Числовые характеристики напряжения в узлах решетчатой модели предлагается определять по полученным авторами формулам
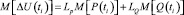 , (4)
, (4)
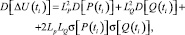 (5)
(5)
где ti – моменты времени, соответствующие вершинам сплайна,
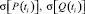 – среднее квадратическое отклонение функций P(t) и Q(t) в узлах сплайна.
– среднее квадратическое отклонение функций P(t) и Q(t) в узлах сплайна.
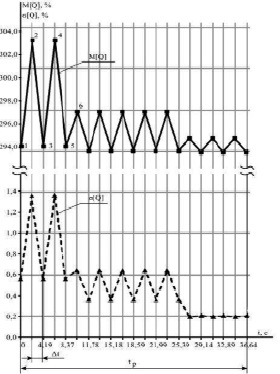
Рис. 3. Полигоны математического ожидания и среднего квадратического отклонения реактивной мощности рабочего цикла нагрузочной диаграммы электроприемника барабанной рубильной машины «Дробилка шпона» фанерного производства
По формулам (4) и (5) определяют числовые характеристики потери напряжения ΔU(ti) в узлах сплайна. Количество экстремумов в графике напряжения равно количеству экстремумов в графике активной мощности, а продолжительность импульсов напряжения Δt равна продолжительности импульсов активной мощности.
По графику изменения напряжения определяются числовые характеристики размахов напряжения δU(ti),
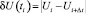 , (6)
, (6)
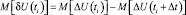 , (7)
, (7)
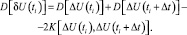 (8)
(8)
Поскольку случайные величины ΔU(ti) и 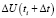 для фанерного производства являются независимыми, то корреляционная функция
для фанерного производства являются независимыми, то корреляционная функция
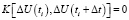 .
.
При этом формула (8) примет вид
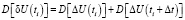 . (9)
. (9)
Дозу фликера авторы рассматривают как случайную величину, которая характеризуется основными числовыми характеристиками: математическим ожиданием 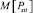 и дисперсией
и дисперсией 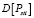 для каждого момента времени ti. Используя аналитический метод расчета, предложенный в [4, 5] и основные положения теории вероятности [2], получены следующие выражения для вычисления
для каждого момента времени ti. Используя аналитический метод расчета, предложенный в [4, 5] и основные положения теории вероятности [2], получены следующие выражения для вычисления 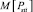 и
и 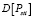 ,
,
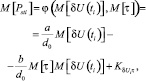 (10)
(10)
где τ – длительность размаха (колебания) напряжения, c,
a, b – коэффициенты, полученные при аппроксимации кривой, определяющей значение коэффициента эквивалентности (FЭ), зависящего от формы колебаний напряжения,
d0 – допустимый размах колебаний напряжения, %,
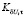 – корреляционный момент,
– корреляционный момент,
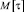 – математическое ожидание длительности размаха (колебания) напряжения, с.
– математическое ожидание длительности размаха (колебания) напряжения, с.
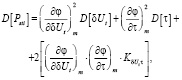 (11)
(11)
где
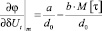 ;
;
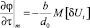 .
.
Величина математического ожидания 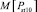 и дисперсии
и дисперсии 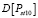 дозы фликера за интервал времени 10 минут, с учетом формул (2, 4, 5), предлагается вычислять по формулам
дозы фликера за интервал времени 10 минут, с учетом формул (2, 4, 5), предлагается вычислять по формулам
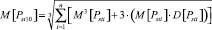 , (12)
, (12)
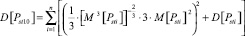 . (13)
. (13)
Зная численные значения величин 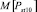 и
и 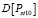 , возможно решить вопросы соответствия требованиям [4], а также выбора методов и параметров устройств для снижения колебаний напряжения.
, возможно решить вопросы соответствия требованиям [4], а также выбора методов и параметров устройств для снижения колебаний напряжения.
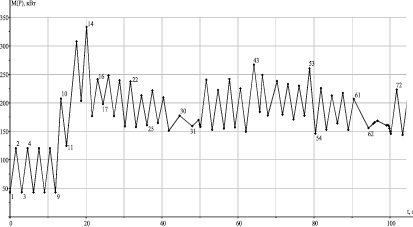
Рис. 4. Фрагмент математической модели группового графика сплайн-функции математического ожидания электрической нагрузки главных приводов механизмов, получающих питание от первой секции шин
В качестве примера использования предложенной методики ниже приводится расчет дозы фликера для секции шин трансформаторной подстанции, питающей фанерное производство. От данной секции получают питание четыре механизма: два лущильных станка, рубительная машина, барабанная рубительная машина «Дробилка карандашей».
Математические модели электрических нагрузок перечисленных механизмов получены на основании выполненных экспериментальных исследований [10]. По разработанной авторами методике, реализованной в виде программы для ЭВМ [11], была получена математическая модель группового графика нагрузки. На рис. 4 приведен фрагмент математического ожидания активной мощности M(P) группового графика нагрузки. Аналогично, авторами были получены групповые графики для математического ожидания реактивной мощности M(Q) и для дисперсии активной D(P) и реактивной D(Q) мощностей.
Ниже приводится пример расчета для двух точек экстремумов (точки 1 и 2, рис. 4) графика напряжения.
В таблице приведены параметры математической модели группового графика нагрузки для экстремумов в точках 1 и 2.
По формуле (4), производится расчет математического ожидания потери напряжения M[ΔU] в точках 1 и 2 группового графика, В,
в точке 1,
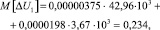
в точке 2,
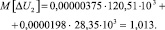
В расчетах принято активное сопротивление – r = 0,0015 Ом; реактивное сопротивление x = 0,00791 Ом; напряжение – Uб = 400, В; линейный оператор активной мощности 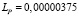 ; линейный оператор реактивной мощности,
; линейный оператор реактивной мощности, 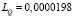 .
.
Математическое ожидание напряжения электрической сети M[ΔU] определяется по формуле (2), для момента времени в точке экстремума 1, В,
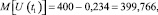
для момента времени в точке экстремума 2, В,
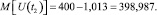
Математическое ожидание размаха напряжения (формула (7)), В,
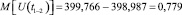 .
.
Математическое ожидание размаха напряжения, %,
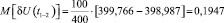 .
.
Дисперсия потери напряжения D[ΔU] в точках экстремума по формуле 5, В2,
в точке 1
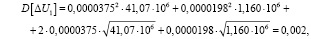
в точке 2
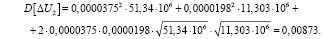
Дисперсия размаха напряжения (формула 8), В2,
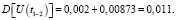
Параметры точек экстремумов группового графика нагрузки
|
Точки экстремумов, i |
Математическое ожидание активной мощности, M(Pi), кВт |
Математическое ожидание реактивной мощности, M(Qi), квар |
Дисперсия активной мощности, D(Pi), кВт2 |
Дисперсия реактивной мощности, D(Qi), квар2 |
|
1 |
42,96 |
3,67 |
41,07 |
1,16 |
|
2 |
120,51 |
28,35 |
51,34 |
11,303 |
Дисперсия размаха напряжения, %,
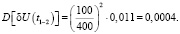
Аналогичным образом производится расчет числовых характеристик для остальных точек экстремумов группового графика напряжения электроприводов, получаемых питание от первой секции шин.
Используя полученные в ходе расчетов данные, применяя формулы (10–13), рассчитываются числовые характеристики кратковременной дозы фликера.
Математическое ожидание дозы фликера для размаха 1–2,
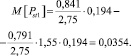
Дисперсия дозы фликера для размаха 1–2,
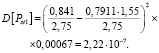
Используя программу, написанную авторами для автоматизации расчетов (проходит процедуру регистрации), производится расчет математического ожидания и дисперсии дозы фликера для остальных размахов. А также данная программа позволяет получить величину кратковременной дозы фликера для интервала времени 10 минут, которая составляет: математическое ожидание – 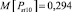 , дисперсия –
, дисперсия – 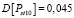 .
.
Выводы
1. Для расчета колебаний напряжения сети и дозы фликера, создаваемых асинхронными электродвигателями с повторно-кратковременным режимом работы и случайной нагрузкой, предлагается описывать электрические нагрузки и напряжения сети решетчатыми моделями, а их математические ожидания и дисперсии интерполировать сплайн-функциями первой степени.
2. Случайная величина дозы фликера является функцией двух случайных аргументов – размаха изменения напряжения и длительности импульса напряжения. Учитывая это, авторами предложены математические выражения для расчета математического ожидания и дисперсии дозы фликера по числовым характеристикам размаха изменения напряжения и длительности импульса напряжения.
3. Предложенную методику расчета дозы фликера рекомендуется использовать для решения методических вопросов и разработки технических мероприятий обеспечения электромагнитной совместимости асинхронных электродвигателей, имеющих резкопеременный характер нагрузки, с питающей их электрической сетью.
Библиографическая ссылка
Черепанов В.В., Калинина Е.А. РАСЧЕТ КРАТКОВРЕМЕННОЙ ДОЗЫ ФЛИКЕРА, ВОЗНИКАЮЩЕЙ ПРИ СТОХАСТИЧЕСКОМ ХАРАКТЕРЕ ИЗМЕНЕНИЯ ЭЛЕКТРИЧЕСКИХ НАГРУЗОК // Фундаментальные исследования. 2016. № 11-5. С. 960-967;URL: https://fundamental-research.ru/ru/article/view?id=41284 (дата обращения: 14.12.2025).



