Одним из эффективных способов повышения долговечности строительных конструкций зданий и сооружений является их антикоррозионная защита с помощью полимерных покрытий, в качестве которых применяются лакокрасочные материалы (ЛКМ) на основе различных синтетических смол. Наибольшее применение в качестве вяжущих ЛКМ находят эпоксидные смолы.
Полимерные покрытия, наносимые по бетонным и металлическим поверхностям, во время эксплуатации очень часто подвергаются негативному воздействию жидких агрессивных сред, повышенных температур и других агрессивных факторов [1–9, 16, 17]. В результате воздействия агрессивных сред у полимерных покрытий, наряду с ухудшением свойств самого материала, снижается адгезионная прочность, а также изменяются декоративные свойства. Это, с одной стороны, обусловливается частичным разрушением физических связей, вклад которых в деформационно-прочностные свойства полимеров весьма существенен, а с другой – выпотеванием и обесцвечиванием отдельных компонентов ЛКМ.
Для улучшения декоративных свойств полимерные покрытия окрашивают различными органическими и неорганическими пигментами, а для повышения их физико-механических свойств и снижения их стоимости в составы ЛКМ добавляют наполнители.
Защитные покрытия должны обладать требуемыми декоративными свойствами, которые должны сохраняться в процессе их эксплуатации. Основными видами старения покрытий вследствие ухудшения декоративных свойств являются: изменение цвета, потеря блеска, появление на поверхности пленки белесоватости.
В настоящее время физико-механические свойства и долговечность эпоксидных защитных покрытий декоративного назначения исследованы недостаточно полно. В литературе не приводятся сравнительные исследования свойств эпоксидных композитов, отверждаемых полиэтиленполиамином и аминофенольным отвердителем, окрашенных и наполненных различными пигментами и наполнителями.
Цель настоящих исследований заключалась в установлении влияния пигментов и наполнителей на стойкость образцов из эпоксидных композитов после выдерживания в условиях климатического старения. Эта задача решалась за счет применения современной испытательной и компьютерной техники.
Стойкость полимерных покрытий оценивалась по изменению показателей твердости, ударной прочности и цветостойкости. Твердость на поверхности образцов определялась инструментальным индентированием. Данная методика разработана сотрудниками ГЦКИ ВИАМ им. Г.В. Акимова [10]. При инструментальном индентировании происходит непрерывное внедрение наконечника в испытуемый образец под действием плавно возрастающей нагрузки с последующим ее снятием и регистрацией зависимости перемещения наконечника от нагрузки. Прослеживая полный цикл нагружения и снятия испытательной нагрузки, определялись значения твердости. При исследовании ударной прочности материалов использовался метод ASTMD 7136 [11]. Для нанесения удара применяли вертикальный копер фирмы Coesfeld, оснащенный полусферическим бойком массой 2,3 кг с диаметром наконечника 10 мм. Высота падения ударного бойка составляла 50 мм. Датчик скорости движения бойка был установлен на расстоянии от 3 до 6 мм над поверхностью образца. Для предотвращения повторного соприкосновения ударника с образцом копер оснащен системой антиотскока.
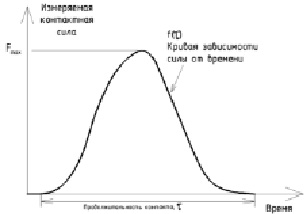
Рис. 1. Модельная кривая зависимости силы ударника от времени
В процессе испытаний фиксировались глубина отпечатка, размеры и площадь зоны повреждения F1, Fmax, E1, Emax. Энергию удара Ei, Дж, определяли по формуле
Ei = CE•h, (1)
где CE = 6,7 – коэффициент нормирования энергии удара на толщину образца, Дж/мм; h – толщина образца, мм.
В момент удара регистрировалась зависимость контактной силы от времени. Пример такой зависимости приведен на рис. 1.
Из зависимости контактной силы от времени была определена величина импульса ударника J, при котором происходило разрушение образца:
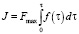 , (2)
, (2)
где Fmax – максимальная сила, зафиксированная в процессе разрушения образца, τ – продолжительность контакта ударника с образцом.
При исследовании цветостойкости использована цветовая модель RGB (Red – красный, Green – зеленый, Blue – синий). Данная модель имеет широкое применение как в компьютерных программных средах (например, MATLAB, Visual C#), так и в различных прикладных исследованиях [12–15], в которых использовалась средняя яркость отдельных составляющих кодов RGB, их изменение по горизонтальному и вертикальному размерам изображений исследуемых образцов.
В данной работе за оценку качества цветовой поверхности принята средняя яркость поверхности отсканированных изображений образцов. Яркость (Bright) изображения рассчитывается по следующей известной формуле:
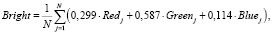 (3)
(3)
где Red, Green, Blue – составляющие кода RGB, N – число пикселей изображения.
Практически, составляющие красного, зеленого и синего берутся для каждого пикселя изображения. При этом предполагается, что геометрические размеры испытуемых образцов имеют одинаковые размеры. Нередко на практике образцы для различных испытаний вырезают из одной пластины. Поэтому возможны расхождения в геометрических, и, следовательно, размерах отсканированных изображений. В наших исследованиях была предусмотрена операция приведения размеров образцов к одному наименьшему размеру. В частности, язык программирования C# на платформе .NET позволяет это сделать без ущерба качества изображения. Возможные малые погрешности рассматриваются в специальных руководствах и здесь не рассматриваются. Во всяком случае, можно отметить, что средние значения кодов RGB имеют отличия в 10–12 знаке после десятичной точки относительно своего исходного размера. Приведение к одному размеру можно осуществлять на основе обрезки изображений. Но в таком случае возможна потеря информации о свойствах на краях образцов. Это еще один довод в пользу программного изменения размеров изображений образцов с сохранением их свойств, в частности средней яркости. Средняя яркость, рассчитанная по приведенной формуле, учитывает особенности световосприятия человеческого зрения – чувствительность человеческого глаза к различным частям спектра.
Составы композиций, принятые для исследований, отличались процентным содержанием в них вяжущего, отвердителей (полиэтиленполиамин и аминофенольный отвердитель), наполнителей (портландцемент и строительный гипс) и пигментов – зеленый (глауконитовый), желтый (железноокислый), оранжевый (свинцовый крон). Образцы изготавливались в виде круглой пластины, диаметром 170 мм и толщиной 10 мм. Составы образцов приведены в табл. 1.
Показатели физико-механических свойств и яркости исследуемых полимерных композитов приведены в табл. 2.
Сравнение полученных результатов показывает следующее. Существует различие показателей в зависимости от используемых компонентов – у композиций с АФ-2 выше модуль упругости и яркость, но твердость и ударная прочность выше у составов, отвержденных ПЭПА. Модуль упругости и твердость выше у состава, наполненного портландцементом, в то же время яркость и ударная прочность больше у материалов, содержащих в качестве наполнителя строительный гипс. Интересные результаты получены при исследовании физико-механических показателей пигментированных составов. Среди сравниваемых материалов более высокие показатели характерны для составов с оранжевым пигментом, а более низкие показатели – с желтым. В то же время сравнение показателей яркости свидетельствует о более высоких их значениях для составов с желтым пигментом.
Различные добавки приводят к различной средней яркости исследуемых образцов (табл. 2). Это дает основание предположить определенную корреляционную связь как между типом добавки, такими показателями, как модуль упругости и твердость вдавливания, с одной стороны, так и определенной зависимости между ними и средней яркостью образцов.
Результаты сканирования контрольных образцов приведены на рис. 2.
Изменения средней яркости контрольных образцов показаны на рис. 3, рис. 4.
На рис. 3, рис. 4 нумерация кривых соответствует табл. 2, в которой испытуемый образец ЭД-20 + АФ-2 кодируется как первый образец.
Образцы испытывались после выдерживания в условиях воздействия ультрафиолетового облучения, переменной влажности и солевого тумана (открытая площадка), повышенной влажности и солевого тумана (под навесом) Черноморского побережья как и в [16, 17]. После испытания образцов, выдержанных в условиях воздействия агрессивных сред получены значения коэффициентов стойкости. Показатели образцов, выдержанных в агрессивных средах, сравнивались с показателями контрольных образцов, хранившихся в помещении испытательной лаборатории. Коэффициенты стойкости образцов, рассчитанные по показателям твердости, модуля упругости, ударной прочности и яркости, приведены в табл. 3.
Таблица 1
Исследуемые составы
|
№ п/п |
Компоненты |
Содержание массовых частей в составах |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
1 |
Эпоксидная смола |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
|
2 |
Полиэтиленполиамин |
10 |
– |
– |
– |
– |
– |
– |
|
3 |
Аминофенольный отвердитель |
– |
10 |
10 |
10 |
10 |
10 |
10 |
|
4 |
Портландцемент |
– |
– |
100 |
– |
– |
– |
– |
|
5 |
Строительный гипс |
– |
– |
– |
100 |
– |
– |
– |
|
6 |
Зеленый пигмент (глауконитовый) |
– |
– |
– |
– |
2 |
– |
– |
|
7 |
Желтый пигмент (железноокислый) |
– |
– |
– |
– |
– |
2 |
– |
|
8 |
Оранжевый пигмент (свинцовый крон) |
– |
– |
– |
– |
– |
– |
2 |
Таблица 2
Результаты исследований контрольных образцов
|
Условия выдерживания образцов |
Состав |
E, МПа |
H, МПа |
Максимальная контактная сила при ударе бойка, Н |
Среднее значение яркости образца |
||
|
Модуль упругости |
Станд. откл. |
Твердость вдавливания |
Станд. откл. |
||||
|
Образцы, выдержанные в помещении лаборатории |
ЭД-20 + ПЭПА |
6,18 |
0,84 |
399 |
8,5 |
3326 |
67,83 |
|
ЭД-20 + АФ-2 |
7,76 |
0,75 |
210,6 |
19,6 |
2688 |
83,68 |
|
|
ЭД-20 + АФ-2 + + строительный гипс |
6,72 |
0,86 |
377,6 |
11,6 |
5395 |
122,77 |
|
|
ЭД-20 + АФ-2 + портландцемент |
10,16 |
0,72 |
462,6 |
3,57 |
3855 |
61,09 |
|
|
ЭД-20 + АФ-2 + зеленый пигмент |
6,35 |
0,86 |
401,3 |
9,24 |
2599 |
61,23 |
|
|
ЭД-20 + АФ-2 + + оранжевый пигмент |
7,02 |
0,79 |
419,5 |
12,46 |
3695 |
71,04 |
|
|
ЭД-20 + АФ-2 + + желтый пигмент |
3,87 |
0,76 |
371,9 |
11,7 |
2920 |
100,47 |
|

Рис. 2. Изображения поверхности контрольных образцов
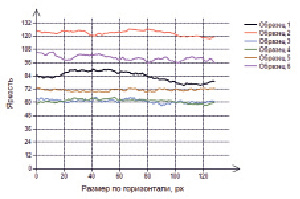
Рис. 3. Средняя яркость контрольных образцов по ширине
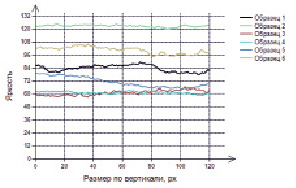
Рис. 4. Средняя яркость контрольных образцов по высоте
Таблица 3
Коэффициенты стойкости исследуемых образцов
|
№ п/п |
Состав образца |
Относительные значения к контрольным образцам |
|||||||
|
Показатели образцов, выдержанных на открытой площадке |
Показатели образцов, выдержанных под навесом |
||||||||
|
Модуль упругости |
Твердость вдавливания |
Максимальная контактная сила |
Среднее значение яркости |
Модуль упругости |
Твердость вдавливания |
Максимальная контактная сила |
Среднее значение яркости |
||
|
1 |
ЭД-20 + ПЭПА |
0,932 |
0,967 |
0,638 |
0,876 |
0,940 |
0,874 |
0,875 |
0,786 |
|
2 |
ЭД-20 + АФ-2 |
0,958 |
0,935 |
0,729 |
0,837 |
0,781 |
0,986 |
0,882 |
0,803 |
|
3 |
ЭД-20 + АФ-2 + строительный гипс |
0,946 |
0,960 |
0,664 |
0,902 |
0,924 |
0,889 |
0,868 |
0,898 |
|
4 |
ЭД-20 + АФ-2 + портландцемент |
0,963 |
0,933 |
0,712 |
1,045 |
0,628 |
0,844 |
0,880 |
1,023 |
|
5 |
ЭД-20 + АФ-2 + зеленый пигмент |
0,946 |
0,960 |
0,768 |
0,984 |
0,940 |
0,941 |
0,788 |
0,923 |
|
6 |
ЭД-20 + АФ-2 + оранжевый пигмент |
0,978 |
0,954 |
0,769 |
0,915 |
0,700 |
0,823 |
0,809 |
1,042 |
|
7 |
ЭД-20 + АФ-2 + желтый пигмент |
0,943 |
0,919 |
0,869 |
0,773 |
0,994 |
0,925 |
0,902 |
0,924 |
Из анализа результатов исследования (табл. 3) можно выделить следующие результаты. После выдерживания образцов всех рассмотренных составов, как на открытой площадке, так и под навесом происходит уменьшение показателей модуля упругости, твердости и яркости на поверхности образцов, а также ударной прочности материалов. Значения коэффициентов стойкости при этом различаются в зависимости от состава лакокрасочных материалов и условий испытания.
Так, сравнение составов, отвержденных полиэтиленполиамином и аминофенольным отвердителем, показывает, что модуль упругости образцов, выдержанных на открытой площадке с ПЭПА ниже, а под навесом, наоборот, в большей степени понизился показатель у материалов, отвержденных АФ-2. Ударная же прочность материалов понизилась в меньшей степени с АФ-2, чем ПЭПА, при обоих условиях экспозиции образцов.
Рассмотрение зависимостей изменения исследуемых показателей у составов с тремя видами пигментов показывает также различие их поведения при выдерживании в условиях климатических воздействий различного типа. При общем характере снижения модуля упругости всех составов из результатов видно, что по стойкости в условиях открытой площадки композиты в зависимости от типа пигмента по убыванию располагаются в следующем порядке – оранжевый, зеленый, желтый, а в случае экспозиции образцов под навесом другое расположение – желтый, зеленый, оранжевый. Для ударной прочности получен следующий порядок расположения пигментов по влиянию на исследуемые показатели: желтый, оранжевый, зеленый при обоих условиях экспозиции образцов. Данные результаты объясняют различную стойкость декоративных составов в зависимости от природы пигмента в средах с различными комплексами воздействий.
Требует тщательного анализа механизм поведения составов, наполненных строительным гипсом и портландцементом. Из результатов исследования следует, что у составов, наполненных портландцементом, падение показателя твердости является более значительным. Падение модуля упругости при выдерживании под навесом также больше у составов в случае их наполнения портландцементом. Ударная прочность образцов в меньшей степени понизилась у композитов, наполненных портландцементом. Изменение средней яркости у составов с портландцементом изменилось в сторону увеличения под навесом и на открытой площадке, что, возможно, объясняется как выравниванием поверхности с течением времени, так и ее осветлением.
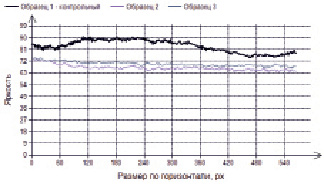
Рис. 5. Средняя яркость по ширине образца ЭД-20 + АФ-2
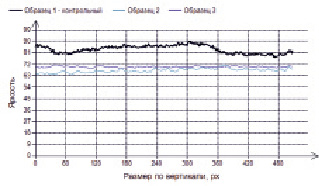
Рис. 6. Средняя яркость по высоте образца ЭД-20 + АФ-2
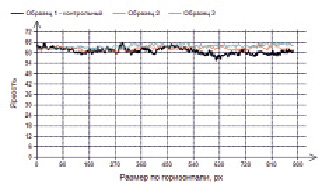
Рис. 7. Средняя яркость по ширине образца ЭД-20 + АФ-2 + портландцемент
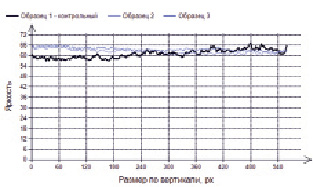
Рис. 8. Средняя яркость по высоте образца ЭД-20 + АФ-2 + портландцемент
Анализ показателя средней яркости исследуемых образцов базируется на подходе, примененном в работах [12–15]. Среднее арифметическое значение яркости может изменяться как по горизонтальному размеру образцов, так и по его вертикали, что влечет за собой определенные отклонения, возможно от желаемого цвета поверхности. При этом дополнительное усреднение каждой кривой даст среднюю яркость по всем пикселям данного изображения. Некоторые примеры изменения средней яркости приведены на рис. 5–8.
На рис. 5–8 график средней яркости контрольного образца – это образец, хранившийся в исследовательской лаборатории архитектурно-строительного факультета Национального исследовательского Мордовского государственного университета имени Н.П. Огарёва.
Образец 2 – отсканированный образец, выдержанный в течение 24 месяцев под навесом на Черноморском побережье. Образец 3 – отсканированный образец, выдержанный также в течение 24 месяцев на открытой площадке Черноморского побережья. Цвета кривых на диаграммах взяты условно для отличия от кривой средней яркости контрольного образца.
Разработанная программа позволяет в автоматизированном режиме получать значения средней яркости для образцов, выбираемых пользователем.
Имеются аналогичные диаграммы для всех типов образцов, приведенные в табл. 2.
Сравнительные показатели образцов из табл. 3 представлены на рис. 9–12, которые сравнивают между собой коэффициенты стойкости, модули упругости, твердости вдавливания, максимальной контактной силы, средней яркости в относительных единицах в зависимости от номера состава образцов. Эти результаты испытаний получены для образцов, выдержанных на открытой площадке и под навесом Черноморского побережья.
Проверим предположение, что между данными в таблице относительных коэффициентов стойкости (табл. 3) существует корреляционная связь. В связи с этим рассчитаем множественные коэффициенты корреляции при линейной регрессионной зависимости между переменными – показателями образцов. Для этого сведем в табл. 4 показатели образцов, выдержанные на открытой площадке и под навесом, матрицу регрессоров, информационную матрицу и значения средней яркости, принятого в качестве функции отклика или исследуемого показателя.
В матрицу регрессоров заложены значения показателей образцов с различной рецептурой (см. табл. 3, табл. 4). Для расчета коэффициентов множественной регрессионной модели принято следующее нормальное уравнение [18]:
(XT•X)•B = XT•Y, (4)
где Т – символ транспонирования, Y – исследуемый показатель (например, средняя яркость).
Если модель наблюдений (матрица Х) полного ранга, то решение нормального уравнения можно осуществить методом Гаусса. В противном случае приходится применять псевдообращение Мура – Пенроуза [19], т.е. разрешить нормальное уравнение, умножив его на псевдообратную матрицу Мура – Пенроуза:
B = (XT•X)–•XT•Y, (5)
где символ «–» означает псевдообращение Мура – Пенроуза.
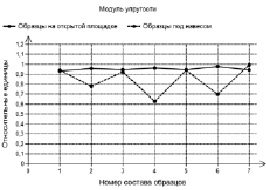
Рис. 9. Сравнение модулей упругости
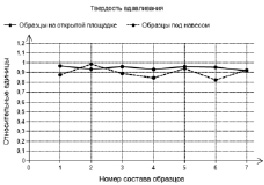
Рис. 10. Сравнение твердости вдавливания
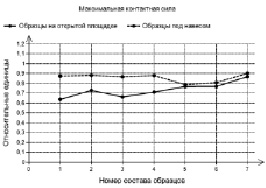
Рис. 11. Сравнение максимальной контактной силы
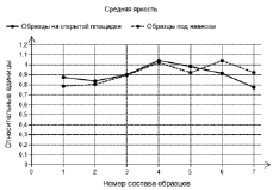
Рис. 12. Сравнение средней яркости
Таблица 4
Расчет схемы уравнения регрессии между показателями образцов
|
Показатели образцов, выдержанные на открытой площадке и под навесом |
Значения матрицы регрессоров Х |
Средняя яркость, значения функции отклика, исследуемого показателя Y |
||
|
Модуль упругости |
Твердость вдавливания |
Максимальная контактная сила |
||
|
0,9320 |
0,9670 |
0,6380 |
1,0000 0,9320 0,9670 0,6380 |
0,8760 |
|
0,9580 |
0,9350 |
0,7290 |
1,0000 0,9580 0,9350 0,7290 |
0,8370 |
|
0,9460 |
0,9600 |
0,6640 |
1,0000 0,9460 0,9600 0,6640 |
0,9020 |
|
0,9630 |
0,9330 |
0,7120 |
1,0000 0,9630 0,9330 0,7120 |
1,0450 |
|
0,9460 |
0,9600 |
0,7680 |
1,0000 0,9460 0,9600 0,7680 |
0,9840 |
|
0,9780 |
0,9540 |
0,7690 |
1,0000 0,9780 0,9540 0,7690 |
0,9150 |
|
0,9430 |
0,9190 |
0,8690 |
1,0000 0,9430 0,9190 0,8690 |
0,7730 |
|
0,9400 |
0,8740 |
0,8750 |
1,0000 0,9400 0,8740 0,8750 |
0,7860 |
|
0,7810 |
0,9860 |
0,8820 |
1,0000 0,7810 0,9860 0,8820 |
0,8030 |
|
0,9240 |
0,8890 |
0,8680 |
1,0000 0,9240 0,8890 0,8680 |
0,8980 |
|
0,6280 |
0,8440 |
0,8800 |
1,0000 0,6280 0,8440 0,8800 |
1,0230 |
|
0,9400 |
0,9410 |
0,7880 |
1,0000 0,9400 0,9410 0,7880 |
0,9230 |
|
0,7000 |
0,8230 |
0,8090 |
1,0000 0,7000 0,8230 0,8090 |
1,0420 |
|
0,9940 |
0,9250 |
0,9020 |
1,0000 0,9940 0,9250 0,9020 |
0,9240 |
|
Информационная матрица XT•X |
Коэффициенты уравнения регрессии |
|||
|
14,0000 12,5730 12,9100 11,1530 12,5730 11,4527 11,6346 9,9745 12,9100 11,6346 11,9348 10,2603 11,1530 9,9745 10,2603 8,9831 |
2,1926 – 0,2282 – 0,7523 – 0,4828 |
|||
Когда регрессионная модель создана, то можно вычислить аппроксимирующую кривую и рассчитать остаточную дисперсию Docm относительно тех же точек, которыми определена, например, средняя яркость. Обозначим выборочную дисперсию исследуемого показателя через D. Тогда множественный коэффициент корреляции () можно рассчитать по следующей формуле [19]:
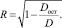 (6)
(6)
Проведенные расчеты сведены в табл. 5.
Как видно из приведенных расчетов, имеется достаточно высокая корреляционная связь между показателями образцов, выдержанных на открытой площадке и под навесом.
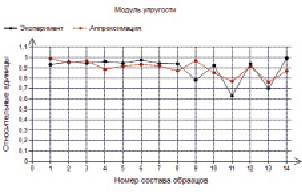
Рис. 13. Аппроксимация показателя «Модуль упругости»
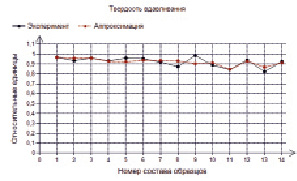
Рис. 14. Аппроксимация показателя «Твердость вдавливания»
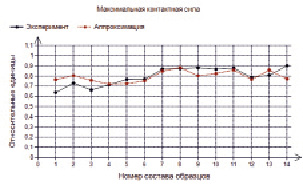
Рис. 15. Аппроксимация показателя «Максимальная контактная сила»
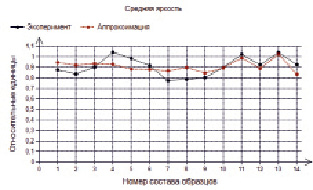
Рис. 16. Аппроксимация показателя «Средняя яркость»
Таблица 5
Коэффициенты линейной регрессионной модели
|
№ п/п |
Свойства |
Значения коэффициентов регрессионной модели |
Значения множественных коэффициентов корреляции |
|||
|
b0 |
b1 |
b2 |
b3 |
|||
|
1 |
Модуль упругости |
0,5255 |
0,9335 |
– 0,2550 |
– 0,3135 |
K1 = 0,7798 |
|
2 |
Твердость вдавливания |
1,1123 |
0,1470 |
– 0,2186 |
– 0,1627 |
K2 = 0,7176 |
|
3 |
Максимальная контактная сила |
2,1297 |
– 0,1609 |
– 0,8761 |
– 0,4186 |
K3 = 0,7940 |
|
4 |
Средняя яркость |
2,1926 |
– 0,2282 |
– 0,7523 |
– 0,4828 |
K4 = 0,8183 |
Для наглядности приведем сравнительные диаграммы табличных данных и аппроксимирующих функций (рис. 13–16).
Приведенные диаграммы аппроксимации построены на основе рассчитанных коэффициентов уравнений регрессии. Например, аппроксимирующая кривая средней яркости (Y) будет определяться уравнением
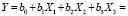
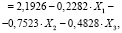 (7)
(7)
где Y – вектор значений средней яркости, – векторы значений модуля упругости, твердости вдавливания, максимальной контактной силы, взятые из табл. 3.
Дисперсия значений исследуемого показателя (например, средней яркости) будет определять собой остаточную дисперсию, которая входит в формулу множественного коэффициента корреляции.
Проведенный анализ показывает достаточно высокую корреляционную зависимость между показателями образцов, которые выдерживались на открытой площадке и под навесом Черноморского побережья. Как и предполагалось, средняя яркость более существенно зависит от показателей модуля упругости, твердости вдавливания, максимальной контактной силы.
Выводы
1. С применением современной испытательной и компьютерной техники исследована стойкость полимерных покрытий на основе эпоксидных связующих в условиях воздействия ультрафиолетового облучения, переменной влажности и солевого тумана, при экспозиции образцов на Черноморском побережье.
2. Предложен метод оценки декоративных свойств с помощью разработанной программы на языке C# в среде разработке Microsoft Visual Studio 2015. Пиксельная обработка изображений отсканированных образцов с целью получения массивов средней яркости проводилась на основе небезопасного кода (unsafe) с помощью указателей с использованием библиотечных классов Bitmap, BitmapData, их методов и свойств.
3. Получены количественные зависимости стойкости эпоксидных композитов от вида отвердителя (полиэтиленполиамин и АФ-2), наполнителя (портландцемент и строительный гипс) и пигмента (желтый, оранжевый и зеленый) по показателям твердости, модуля упругости, ударной прочности и цвета. Выявлены лакокрасочные и тонкозернистые составы с улучшенными показателями твердости, ударной прочности, цветостойкости и требуемой деформативности.
4. Выполнен корреляционный анализ взаимосвязи относительной стойкости полученных результатов по различным видам испытаний и найдены аппроксимирующие функции. Установлена достаточно высокая корреляционная связь между показателями образцов, выдержанных в условиях ультрафиолетового облучения, переменной влажности, солевого тумана (открытая площадка морского побережья) и повышенной влажности, солевого тумана (воздушные условия «под навесом» морского побережья).
5. Эпоксидные композиты, составленные с применением вышеуказанных компонентов, обладают повышенными показателями физико-химического сопротивления и могут быть использованы в качестве защитных покрытий по строительным конструкциям, клеевых составов и в качестве связующих для полимербетонов.
Библиографическая ссылка
Ерофеев В.Т., Смирнов И.В., Воронов П.В., Афонин В.В., Каблов Е.Н., Старцев О.В., Старцев В.О., Медведев И.М. ИССЛЕДОВАНИЕ СТОЙКОСТИ ПОЛИМЕРНЫХ ПОКРЫТИЙ В УСЛОВИЯХ ВОЗДЕЙСТВИЯ КЛИМАТИЧЕСКИХ ФАКТОРОВ ЧЕРНОМОРСКОГО ПОБЕРЕЖЬЯ // Фундаментальные исследования. 2016. № 11-5. С. 911-924;URL: https://fundamental-research.ru/ru/article/view?id=41277 (дата обращения: 10.03.2026).



