Метод многочастотной электроимпедансной томографии (ЭИТ) основан на использовании нелинейной зависимости проводимости σ и диэлектрической проницаемости ε биологических тканей от частоты инжектируемого тока, что позволяет получать дополнительную информацию, например оценить соотношение внутриклеточной и межклеточной жидкостей [4]. Для практической реализации данного метода необходимы технические и программные средства проведения измерений на поверхности биологического объекта (БО) и обработки результатов, которые позволят реконструировать и визуализировать картину распределения электрических параметров в томографическом сечении. При этом появляется возможность идентифицировать отдельные внутренние структуры и физиологические процессы, протекающие в БО. Для решения задач многочастотной ЭИТ предлагается применить теорию натурно-модельного подхода, предложенного в [1]. В этой связи необходимо проведение исследований применимости данного подхода и определения его ограничений.
Цель исследования
Целью исследования является определение условий, требуемых для применения натурно-модельного подхода для реконструкции проводимости биологического объекта.
Материалы и методы исследования
Для достижения поставленной цели построена компьютерная модель исследуемой области БО, применены численные методы: метод конечных элементов, реализованный в программном пакете Femm 4.2, метод оптимизации Хука – Дживса. Для объяснения полученных результатов построена поверхность, отражающая зависимость невязки значений потенциалов на электродах.
Важнейшей составляющей ЭИТ является обратная задача реконструкции распределения удельных электрических характеристик в объеме исследуемого БО. Существенное влияние на результат такой реконструкции оказывает выбор математической модели электромагнитного поля. В общем случае оно описывается уравнениями Максвелла (в дифференциальной форме) [6]:
, 
,
, 
,
, 
, 
,
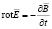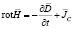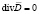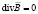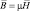где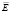 
– напряженность электрического поля, 
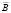– магнитная индукция, 
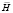– напряженность магнитного поля, 
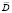– вектор электрического смещения, 
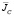– плотность наводимых полем токов проводимости, μ – магнитная проницаемость, t – время. Здесь учтено, что в области исследуемого объекта свободные заряды отсутствуют.
При инжектировании гармонического тока I потенциал φi, измеряемый на каждом электроде после окончания переходных процессов, будет являться синусоидальным сигналом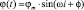 
, где φm – амплитуда тока,ω – круговая частота, связанная с частотой по формуле 
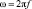, Φ – смещение фазы относительно тока источника. Для получения полной информации о потенциале в этом случае необходимо использовать фазочувствительный вольтметр [1]. Система уравнений Максвелла сводится к уравнению Лапласа относительно комплексной амплитуды 
скалярного электрического потенциала:
, (*)
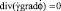где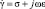 
– комплексная удельная проводимость, j – мнимая единица.
Применительно к решению обратных задач идентификации, к которым относится задача реконструкции проводимости, натурно-модельный подход сводится к поиску значений параметров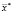 
системы, доставляющих минимум функционалу невязки 
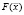. При этом поиск осуществляется согласно некоторому итерационному алгоритму, задающему движение от начального приближения 
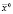к вектору оптимальных значений 
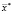, причем на каждой итерации производится решение прямой задачи расчета поля для каждого вектора значений параметров 
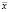[2].
В основу работы положено проведение численных экспериментов. Для решения прямой задачи согласно уравнению (*) использовался программный пакет конечноэлементного анализа Femm 4.2. В качестве минимизируемого функционала F была выбрана невязка амплитуд потенциалов на электродах при различных конфигурациях инжектирующих электродов:
,
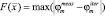где m – номер измерения, φmeas – результат измерения потенциалов в искомой точке, φiter – результат измерения потенциалов на текущей итерации.
Так как вычисление значений потенциалов на электродах выполняется численно с помощью стороннего программного пакета, то для минимизации функционала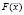 
возможно использовать только методы минимизации нулевого порядка, не требующие знания частных производных 
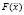по каждому варьируемому параметру. В силу этих причин в работе использовался метод конфигураций (метод Хука – Дживса) [3], являющийся методом нулевого порядка многомерной оптимизации. Метод конфигураций представляет собой комбинацию исследующего поиска с циклическим изменением переменных и ускоряющего поиска по образцу и позволяет найти безусловный минимум целевой функции 
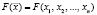n переменных. Исследующий поиск направлен на выявление локального поведения целевой функции в текущей точке и определение направления убывания, вдоль которого затем выполняется движение на этапе ускоряющего поиска.
Алгоритм метода конфигураций заключается в следующем
1. Задаются: начальная точка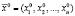 
; минимальные значения шагов εi > 0, i = 1,…, n, при достижении которых алгоритм завершается; начальные значения шагов по направлениям Δi > δi, i = 1,…, n; коэффициент уменьшения шага α > 1; ускоряющий множитель λ > 0, используемый на этапе ускоряющего поиска. Счетчик итераций k = 0, в качестве направления исследующего поиска выбирается координатный вектор, соответствующий первой координате i = 1, в качестве базовой точки исследующего поиска выбирается начальная точка 
.
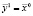2. Выполняется исследующий поиск по выбранному координатному направлению i.
2.1. Производится шаг в сторону возрастания xi на величину Δi. Если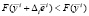 
, где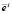 
– орт, соответствующий выбранному направлению i, то шаг считается удачным, 
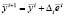и выполняется переход к пункту 3.
2.2. Если в пункте 2.1 шаг неудачен, то производится шаг в сторону убывания xi на величину Δi. Если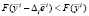 
, где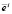 
– орт, соответствующий выбранному направлению i, то шаг считается удачным, 
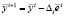и выполняется переход к пункту 3.
2.3. Если в пунктах 2.1 и 2.2 шаги неудачны, то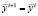 
.
3. Выполняется проверка условий.
3.1. Если i < n, то исследующий поиск по направлениям продолжается (i =i + 1, переход к пункту 2).
3.2. Если i = n, то проверяется успешность исследующего поиска: если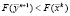 
, переход к пункту 4, иначе – к пункту 5.
4. Полагают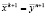 
, после чего проводится поиск по образцу: 
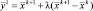и выполняется переход к следующей итерации k =k + 1 и исследующему поиску i = 1 (на пункт 2).
5. Проверка условий завершения работы алгоритма.
5.1. Если величины шагов по каждому координатному направлению не превышают заданную величину Δi ≤ δi, i = 1,…, n, то решение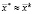 
найдено.
5.2. Если некоторые Δi > δi, то они уменьшаются: Δi = Δi/α. Затем выполняется переход к следующей итерации: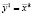 
, 
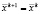, k =k + 1, i = 1 и исследующий поиск выполняется заново с уменьшенными значениями шагов (на пункт 2).
Результаты исследования и их обсуждение
Приведенный алгоритм метода Хука – Дживса был реализован в виде скрипта в среде Octave. Для решения прямой задачи электроимпедансной томографии применялся пакет моделирования Femm 4.2, в котором автоматически задавалась и решалась серия плоскопараллельных задач. Пример одной из задач и визуализация результатов вычисления представлены на рис. 1. Область расчета D0 (модель фантома) представляет собой круг диаметром 17 см с включенной неоднородностью D1 в виде круга диаметром 4 см. Реализованный скрипт предусматривает возможность указания неточечных электродов с заданным радиусом, однако реализация процесса получения результатов моделирования для контура занимает много больше времени для выбранного пакета моделирования. Поэтому при моделировании использовались точечные электроды. Реализована следующая стратегия получения измерительных данных. Электрод E1 обозначается как точка с нулевым потенциалом, электрод E2 обозначается как точечный источник тока силой 5 мА. Измеряются потенциалы φ1..φ16 на электродах E1..E16. Далее электрод E2 обозначается как точка с нулевым потенциалом, электрод E3 – как источник тока. Измеряются потенциалы φ1..φ16 на электродах E1..E16 относительно общей точки. И так далее до тех пор, пока электрод E16 будет обозначен как точка с нулевым потенциалом, а электрод E1 – как источник тока. В итоге для числа электродов N = 16 получается 256 измеренных значений. Нумерация электродов – с 12 часов, движение по часовой стрелке.
Проводимости подобластей были зафиксированы σ0 = 1,47 См/м, σ1 = 10–6 См/м. Данные значения проводимости соответствуют биологическим тканям – мышечной и костной. В качестве относительных диэлектрических проницаемостей были заданы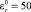 
и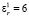 
. Частота инжектируемого тока была принята равной 1 кГц. Варьируемыми параметрами модели были координаты центра области неоднородного включения 
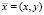. В качестве источника данных об измеренных значениях потенциалов на электродах выступали результаты решения прямой задачи моделирования поля с координатами центра включения 
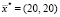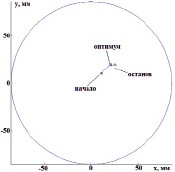
, мм. Реализованный алгоритм приводил к верному результату не во всех случаях, соответствующих разным начальным приближениям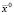 
. Так, при движении от точки 
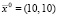мм, начальном шаге Δ = (10, 10) мм, коэффициенте уменьшения шага α = 2 и ускоряющем множителе λ = 2, минимальных значениях шагов δ = (1, 1) мм) алгоритм останавливался в искомой точке 
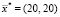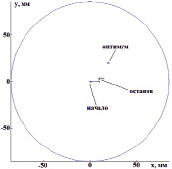
мм, потратив на движение 6 итераций (рис. 2, а). При движении из другой начальной точки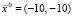 
мм и тех же значениях параметров, применение алгоритма приводило к неправильному результату – точке 
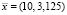мм.
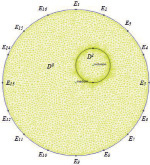
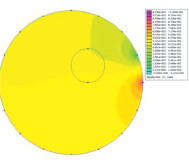
Рис. 1. Область расчета модельной задачи и визуализация результатов расчета
а)
б)
Рис. 2. Траектории поиска решения методом Хука – Дживса применительно к задаче реконструкции проводимости БО. Удачный поиск (а), неудачный поиск (б)
а)
б)
в)
г)
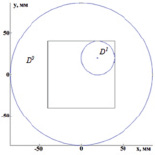
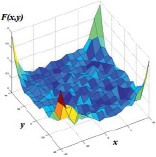
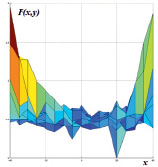
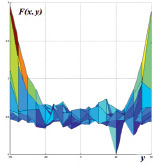
Рис. 3. Область построения диаграммы (а). Диаграмма зависимости невязки значений потенциалов на электродах от координат центра области, занимаемой включением (б, в, г )
Полученные результаты могут быть объяснены с помощью диаграммы зависимости невязки значений потенциалов на электродах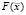 
от координат 
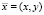центра области D1, занимаемой включением. На рис. 3, а показана область построения диаграммы. Из диаграммы на рис. 3, б видно, что функционал F(x, y) имеет глобальный минимум в точке 
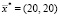мм и множество локальных минимумов. В угловых точках рассмотренной области наблюдается значительный рост невязки, что вызвано приближением неоднородности D1 к границе фантома. Таким образом, только при таком выборе начального приближения 
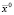, когда оно находится близко к искомой точке 
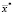, алгоритм будет приводить к правильному результату. В противном случае метод будет останавливаться в одной из точек локального минимума.
Выводы
Полученные результаты могут быть обобщены на методы поиска (оптимизации) в целом, так как, исходя из знания только локальной информации, невозможно гарантированно прийти в точку глобального минимума. Таким образом, предлагаемый натурно-модельный подход не рекомендуется применять для таких постановок, когда в процессе решения обратной задачи предполагается смещать границы внутренних структур БО. В этом случае необходимо использовать специальные методы регуляризации [5], так как последние не включают в себя этап решения прямой задачи. Использование готовых программных решений, предназначенных для моделирования поля (решения прямой задачи), также является затруднительным в этом случае, что требует разработки специальных программ. Следовательно, для реализации натурно-модельного подхода, сводящегося при решении обратных задач идентификации к таким методам поиска, необходимо разработать алгоритмы определения начальных значений электрических характеристик в томографическом сечении. Кроме того, данный подход может быть применен также и на других этапах решения обратной задачи многочастотной электроимпедансной томографии.
Работы выполняются при поддержке Российского фонда фундаментальных исследований в рамках гранта «мол_а_дк» № 16-38-60173.
Библиографическая ссылка
Алексанян Г.К., Денисов П.А., Кучер А.И. ИССЛЕДОВАНИЕ ПРИМЕНИМОСТИ НАТУРНО-МОДЕЛЬНОГО ПОДХОДА ДЛЯ ЗАДАЧ РЕКОНСТРУКЦИИ ПОЛЯ ПРОВОДИМОСТИ ПРИ МНОГОЧАСТОТНОЙ ЭЛЕКТРОИМПЕДАНСНОЙ ТОМОГРАФИИ // Фундаментальные исследования. – 2016. – № 11-5. – С. 895-899;URL: https://fundamental-research.ru/ru/article/view?id=41274 (дата обращения: 18.04.2024).