При решении ряда прикладных задач, например, задачи теории дифракции акустических и электромагнитных волн, возникает необходимость решения СЛАУ с комплексной матрицей коэффициентов ленточной структуры. При решении одномерных задач в качестве метода решения сеточных уравнений с матрицей ленточного вида используется экономичный метод прогонки. В случае двух и большего числа пространственных измерений существуют варианты метода прогонки, которые не являются экономичными, поэтому разработка итерационного метода решения сеточных уравнений актуальна.
Итерационные методы решения сеточных уравнений
При решении уравнений сеточными методами возникает необходимость решения системы линейных алгебраических уравнений следующего вида:
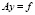 , (1)
, (1)
где 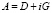 , G – самосопряженный положительно определенный оператор (
, G – самосопряженный положительно определенный оператор (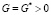 ), D – диагональный, положительно определенный оператор. Уравнения вида (1) рассматривались ранее [1–3], причем предполагалось, что оператор A имеет вид
), D – диагональный, положительно определенный оператор. Уравнения вида (1) рассматривались ранее [1–3], причем предполагалось, что оператор A имеет вид
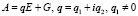 .
.
Поставим задачу разработки адаптивного метода решения СЛАУ (1) для случая 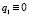 . Такая постановка связана с тем, что применение адаптивных методов не требует априорной информации об операторе задачи. Для решения системы (1) используем нестационарный двухслойный итерационный процесс:
. Такая постановка связана с тем, что применение адаптивных методов не требует априорной информации об операторе задачи. Для решения системы (1) используем нестационарный двухслойный итерационный процесс:
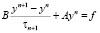 ,
, 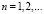 (2)
(2)
где B – положительный самосопряженный оператор, 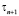 – итерационный параметр.
– итерационный параметр.
Из формулы (2) выразим 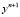 :
:
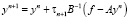 . (3)
. (3)
Обозначим 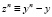 погрешность решения уравнения на n-м шаге. Уравнение (3) в терминах погрешности zn на n-м шаге для погрешности примет вид
погрешность решения уравнения на n-м шаге. Уравнение (3) в терминах погрешности zn на n-м шаге для погрешности примет вид
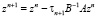 .
.
Оптимизация итерационного параметра τ
Для получения оценок скорости сходимости будем использовать Эрмитову норму: 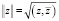 , где
, где 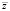 – вектор, комплексно сопряженный вектору z.
– вектор, комплексно сопряженный вектору z.
Введем обозначение 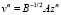 . Вследствие того, что действительная часть оператора
. Вследствие того, что действительная часть оператора 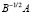 положительно определена, он не вырожден, из сходимости последовательности vn к нулю следует сходимость последовательности zn к нулю. Запишем норму вектора v на (n + 1)-м итерационном слое:
положительно определена, он не вырожден, из сходимости последовательности vn к нулю следует сходимость последовательности zn к нулю. Запишем норму вектора v на (n + 1)-м итерационном слое:
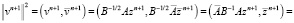
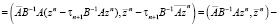
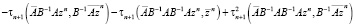 .
.
Обозначим 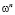 вектор поправки (
вектор поправки (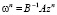 ), тогда последнее равенство примет вид
), тогда последнее равенство примет вид
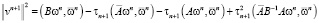 .
.
С учетом равенства 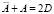 норму вектора погрешности запишем в следующем виде:
норму вектора погрешности запишем в следующем виде:
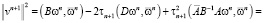
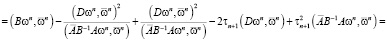
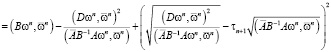 .
.
Норма вектора погрешности минимальна в случае, когда
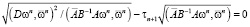 .
.
Следовательно,
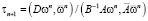 . (4)
. (4)
Выбор оптимального оператора предобуславливателя B
Представим знаменатель (4) в виде
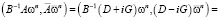
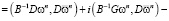
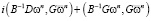 .
.
Мнимая часть последнего выражения равна нулю, так как оператор 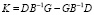 – кососимметричный. С учетом введенного обозначения последнее выражение примет вид
– кососимметричный. С учетом введенного обозначения последнее выражение примет вид
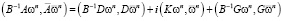 .
.
Подставляя его в формулу (4), получим значение итерационного параметра 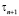 :
:
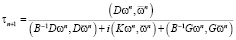 . (5)
. (5)
Оценим скорость сходимости разработанного алгоритма.
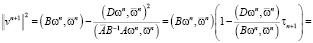
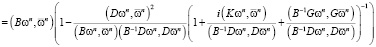 .
.
Заметим, что в силу неравенства Коши-Буняковского
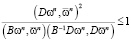 ,
,
причем равенство достигается при B = D.
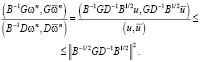
Минимум полученной оценки достигается при B = D, так как:
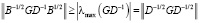 ,
,
где 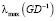 – максимальное собственное число оператора GD–1. Выражение
– максимальное собственное число оператора GD–1. Выражение
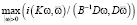
принимает минимальное нулевое значение при B = D. Таким образом, для обеспечения максимальной скорости сходимости метода в качестве оператора B нужно использовать диагональный оператор D. С учетом этого выражение (5) для 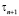 , при котором скорость сходимости максимальна, примет вид
, при котором скорость сходимости максимальна, примет вид
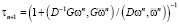 . (6)
. (6)
Скорость сходимости метода
Оценка скорости сходимости разработанного алгоритма с учетом равенства B = D имеет вид
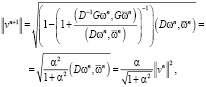
где 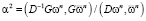 .
.
Оценим α:
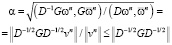 .
.
При решении прикладных задач, как правило, 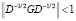 . Норма оператора
. Норма оператора 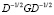 зависит от шага дискретизации по временной переменной. В работе [7] показана зависимость погрешности от шага дискретизации по временной переменной для уравнения диффузии, при этом следует следить за выполнением условия монотонности явной схемы.
зависит от шага дискретизации по временной переменной. В работе [7] показана зависимость погрешности от шага дискретизации по временной переменной для уравнения диффузии, при этом следует следить за выполнением условия монотонности явной схемы.
Алгоритм метода решения сеточных уравнений с матрицей коэффициентов вида A = D + iG
1) Задаем матрицы G, D и вектор f.
2) Задаем начальное приближение решения yn при n = 0, допустимое значение погрешности решения (нормы вектора поправки).
3) Считаем вектор поправки w по формуле 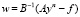 , B = D.
, B = D.
4) Находим векторы 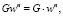
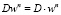 ,
, 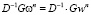 .
.
5) Выполняем комплексное сопряжение для векторов 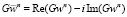 ,
, 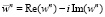 .
.
6) Вычисляем скалярные произведения 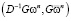 и
и 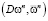 .
.
7) Рассчитываем итерационный параметр 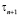 по формуле:
по формуле:
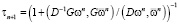 .
.
8) Находим приближенное решение на следующей итерации 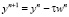 .
.
9) Если норма вектора поправки больше заданного значения, то наращиваем n и возвращаемся в пункт 3.
10) Конец работы алгоритма.
Пример использования метода для решения задачи бегущей волны
Для описания распространения звуковых пучков в квазиоптическом приближении используют уравнение [1, 2]:
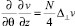 (7)
(7)
с начальным условием:
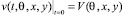
и граничными условиями периодичности сигнала [3]:
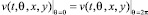 ,
,
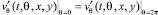 ;
;
симметричности:
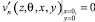 ;
;
отсутствия энергии в бесконечно удаленной точке:
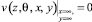 ,
,
где 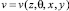 – величина скорости частиц среды, θ – время в сопровождающей системе координат, z – нормированное расстояние, N – параметр уравнения, характеризующий дифракцию волнового пучка,
– величина скорости частиц среды, θ – время в сопровождающей системе координат, z – нормированное расстояние, N – параметр уравнения, характеризующий дифракцию волнового пучка, 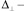 поперечный лапласиан.
поперечный лапласиан.
Решение задачи (7) находится методом гармоник (тригонометрическая интерполяция). Функцию скорости частиц среды можно представить усеченным рядом Фурье, полученным в результате применения тригонометрической интерполяции:
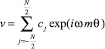 , (8)
, (8)
где ω – частота первой гармоники, m – номер гармоники, N – количество дискретных значений величины скорости частиц среды на период. Так как функции 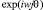 для различных j линейно независимы, то получим уравнение
для различных j линейно независимы, то получим уравнение
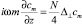 .
.
Для построения решения разностной схемы вводится равномерная сетка:
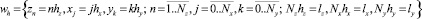 ,
,
где n, j, k – индексы по направлениям z, x, y соответственно; hz, hx, hy – шаги по направлениям z, x, y соответственно; Nz, Nx, Ny – количество узлов сетки по направлениям z, x, y соответственно; lx, ly, lz – размеры расчетной области.
Дискретный аналог оператора диффузионного переноса 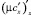 , учитывающий частичную заполненность ячеек в случае граничных условий в форме Неймана, имеет вид
, учитывающий частичную заполненность ячеек в случае граничных условий в форме Неймана, имеет вид
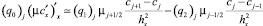 ,
,
где qi – коэффициенты, описывающие заполненность контрольных областей [6].
Дискретный аналог задачи распространения звуковых пучков запишем в виде
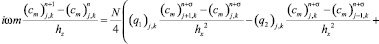
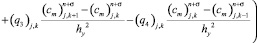 , (9)
, (9)
где σ – весовой коэффициент схемы [4].
В работе [8] рассмотрена конечно-разностная аппроксимация данного уравнения на основе схем с весами и доказана его устойчивость в случае σ ≥ 0,5. Решение уравнения (7) сеточными методами существенно менее трудозатратно по сравнению с решением исходной волновой задачи [5]. Решение дискретной задачи (9) сводится к решению сеточного уравнения с оператором вида A = D + iG. Рассмотрены гармонические пучки с начальным гауссовским распределением:
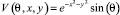 .
.
На рисунке представлено решение задачи при следующих параметрах: N = 0,025, lx = 0,5, ly = 0,5, lz = 0; 0,25; 0,5; 1. Показано сечение .
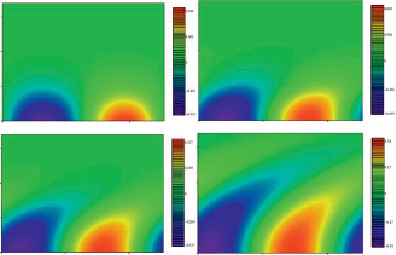
Решения задачи распространения звуковых пучков
Рисунок иллюстрирует, как с ростом z происходит диффузия амплитуды поля в поперечном направлении к оси пучка и трансформация первоначально плоского волнового фронта в квазисферический.
Заключение
В работе предложен вариант метода минимальных поправок в случае комплексной матрицы коэффициентов. Получено выражение для оптимального вида оператора предобуславливателя B. Получена теоретическая оценка скорости сходимости. Рассмотрен пример применения предложенного метода. Показано, что теоретическая оценка скорости сходимости хорошо согласуется с реальной погрешностью решения.
Работа выполнена при финансовой поддержке РФФИ по проектам № 15-07-08626, №15-07-08408, № 16-3716-37-00129, № 15-01-08619.
Библиографическая ссылка
Чистяков А.Е., Сухинов А.И., Кузнецова И.Ю., Проценко С.В., Яковенко И.В. РАЗРАБОТКА АДАПТИВНОГО МЕТОДА МИНИМАЛЬНЫХ ПОПРАВОК ДЛЯ РЕШЕНИЯ СИСТЕМЫ СЕТОЧНЫХ УРАВНЕНИЙ С ОПЕРАТОРОМ СПЕЦИАЛЬНОГО ВИДА // Фундаментальные исследования. 2016. № 11-4. С. 746-751;URL: https://fundamental-research.ru/ru/article/view?id=41249 (дата обращения: 13.03.2026).



