Электроконвекция (ЭК) – это движение раствора, вызванное воздействием электрического поля на пространственный заряд, локализованный вблизи межфазной ионоселективной границы. Явление ЭК имеет значение в большом количестве практических приложений, таких как электромембранные устройства опреснения и разделения, аналитической химии, микро-/ нанофлюидики [9]. Установлено, что имеется экономическая целесообразность функционирования таких систем в сверхпредельных токовых режимах [9]. Экспериментальные [1, 13] и теоретические исследования [5, 12, 14] показывают, что основным механизмом сверхпредельного переноса ионов в мембранных системах является электроконвекция.
Для описания ЭК С.С. Духин и Н.А. Мищук ввели понятия электроосмоса первого и второго родов [2, 4]. Электроосмос первого рода возникает в результате действия внешнего электрического поля на равновесный двойной электрический слой (ДЭС), который существует даже при отсутствии электрического тока. Электроосмос второго рода вызван действием электрического поля на расширенную область пространственного заряда (ОПЗ), возникающую при сверхпредельных плотностях тока.
В мембранных системах без вынужденного течения выделяют два режима ЭК. В случае искривленной или электрически неоднородной поверхности при допредельных токах, тангенциальное электрическое поле вызывает стабильный электроосмотический перенос, описанный в работах Духина и Мищук [4, 6, 7]. В случае однородных идеально селективных мембран в отсутствие вынужденного течения жидкости такой режим не реализуется: ЭК появляется в результате гидродинамической неустойчивости при сверхпредельных токах, что показали И. Рубинштейн и Б. Зальцман [12].
В мембранных системах с вынужденным течением, например, электродиализных каналах (ЭД), концентрация распределяется неравномерно по длине канала: по мере продвижения раствора между мембранами концентрация электролита уменьшается, а толщина диффузионного слоя увеличивается. В отличие от механизма, описанного Духиным и Мищук, тангенциальная сила, необходимая для электроосмоса первого рода, возникает не вследствие электрической неоднородности поверхности, а вследствие неоднородности продольного распределения концентрации [15]. В этом режиме допредельных токов объемная сила локализуется на сравнительно небольшом расстоянии от мембраны, где из-за условия прилипания вязкостные силы играют важную роль. Вклад ЭК в повышение массопереноса становится значительным только при напряжениях, соответствующих i > ilim, когда развивается неравновесная ЭК (электроосмос второго рода). В этом случае толщина ОПЗ резко возрастает по сравнению с равновесным двойным слоем и становится порядка сотен нанометров [14]. На таких расстояниях роль вязкостных сил снижается. Поэтому основной вклад в развитие сверхпредельного переноса принадлежит электроосмосу второго рода.
Таким образом, развитие электроконвекции определяется структурой ДЭС у поверхности мембран. Толщина области ДЭС для реальных систем – малая величина, для нее характерны большие значения градиентов концентрации, электрического потенциала и скорости, поэтому ее численное описание требует значительных вычислительных затрат [10]. Для оптимизации математической электроконвекции в мембранных системах необходим анализ граничных условий у поверхности. Целью данного исследования является оценка точности и эффективности граничных условий первого и второго родов (условия Дирихле и Неймана) на концентрацию противоионов у поверхности ионоселективных мембран.
Математическая модель
Рассмотрим двумерную модель массопереноса в камере обессоливания (КО) ЭД ячейки, содержащей анионообменную (АОМ) и катионообменную (КОМ) мембраны (рис. 1). Здесь х – поперечная в отношении вынужденного течения координата, изменяющаяся от 0 (граница с АОМ) до Н (граница с КОМ); y – продольная координата, изменяющаяся от 0 (вход в канал) до L (выход из канала).
Математическая модель включает систему сопряженных уравнений Нернста–Планка–Пуассона–Навье–Стокса, которая для бинарного электролита записывается следующим образом [15]:
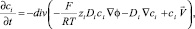
i = 1, 2, (1)
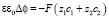 , (2)
, (2)
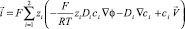 , (3)
, (3)
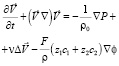 , (4)
, (4)
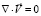 (5)
(5)
где Di, zi и ci – коэффициент диффузии, зарядовое число и молярная концентрация i-го иона, соответственно; φ – электрический потенциал; t – время; 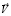 – скорость потока раствора; ρ0 – плотность раствора (предполагается постоянной); P – давление; ε0 – электрическая постоянная; ε – относительная диэлектрическая проницаемость раствора электролита (предполагается постоянной); ν – кинематическая вязкость; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура. Здесь P,
– скорость потока раствора; ρ0 – плотность раствора (предполагается постоянной); P – давление; ε0 – электрическая постоянная; ε – относительная диэлектрическая проницаемость раствора электролита (предполагается постоянной); ν – кинематическая вязкость; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура. Здесь P, 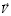 , φ,
, φ, 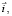 c1 и c2 – неизвестные функции t, x и y.
c1 и c2 – неизвестные функции t, x и y.
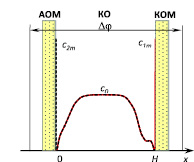
Рис. 1. Схематичные концентрационные профили в КО ЭД ячейки с АОМ и КОМ. c0 – входная концентрация раствора электролита, c1m и c2m – концентрации катионов у поверхности КОМ и анионов у поверхности АОМ, Δφ – полный скачок потенциала (СП)
Электрический режим определяется заданием СП Δφ между двумя эквипотенциальными плоскостями, проходящими параллельно мембранам в КК слева и справа от центральной КО. При расчете вольтамперной характеристики (ВАХ) электродиализного канала скорость развертки Δφ во времени равнялась 0,01 В/с, что обеспечивало квазистационарный режим.
На условных границах АОМ/раствор (x = 0, y∈[0, L]) и раствор/КОМ (x = H, y∈[0, L]) для концентрации противоионов мы применяли два типа условий. Граничное условие первого рода (условие Дирихле), изначально использованное И. Рубинштейном и Л. Штильманом [11]: концентрация противоионов задается постоянной, в N раз больше концентрации в объеме раствора (Na для АОМ, Nc для КОМ). Указывается, что это условие асимптотически верно для Nc >> 1 [11].
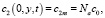
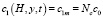 . (6)
. (6)
Условие второго рода (условие Неймана) [15]:
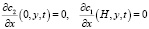 . (7)
. (7)
При использовании условия (6), предполагается, что условная граница раствор/мембрана проходит между диффузной и компактной частями ДЭС, то есть граница перемещается в положение, соответствующее минимальному значению концентрации противоионов в обедненном растворе. Обоснование условия (7) следует из условия квазиравномерного распределения плотности пространственного заряда (КРЗ), предложенного М.Х. Уртеновым и соавт. [14]. Согласно этому условию градиент плотности пространственного заряда считается малым. Предположение КРЗ приводит к корректному описанию распределения концентрации противоионов и коионов везде в неподвижном диффузионном слое, кроме квазиравновесной части ДЭС [14].
На этих же границах задаются значения электрического потенциала. Мембраны предполагаются непроницаемыми для коионов. Скорость жидкости на границах раствор/мембрана принимается равной нулю (условие прилипания). Таким образом,
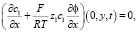 (8)
(8)
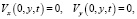 (9)
(9)
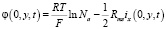 , (10)
, (10)
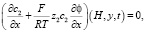 (11)
(11)
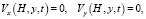 (12)
(12)
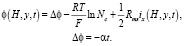 (13)
(13)
Здесь α – скорость развёртки СП; c0 – концентрация в объеме раствора как в КО, так и в камере концентрирования (КК). φ(0, y, t) рассчитывается как сумма омических сопротивлений раствора в левой КК и в объеме АОМ, к которой прибавляется сумма двух межфазных СП на АОМ, уравнение (10); Rms/2 – омическое сопротивление этой части системы. Межфазные СП находятся из соотношений Доннана без учета градиента концентрации в мембране. Аналогично получается уравнение (13) для φ(Н, y, t). Вычитая уравнение (13) из (10), можно получить следующее выражение для СП между эквипотенциальными плоскостями, изображенными на рис. 1 [15]:
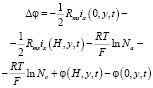
из которого видно, что Δφ представляет собой сумму следующих слагаемых:
1) омических СП в частях системы, в которых не происходит концентрационная поляризация и имеющих суммарное сопротивление Rms;
2) доннановских СП на межфазных границах обеих мембран (это слагаемое исключает влияние СП в отбрасываемой части ДЭС при применении условия второго рода);
3) СП в КО между точками x = 0 и x = H.
Условия на входе в канал (x∈[0, H], y = 0), на выходе (x∈[0, H], y = L) и при t = 0 аналогичны условиям, принятым в [15].
Средняя плотность тока в канале вычисляется по формуле
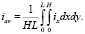 (14)
(14)
Плотность тока нормирована на предельную плотность тока, определяемую уравнением Левека [8]:
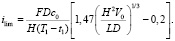 (15)
(15)
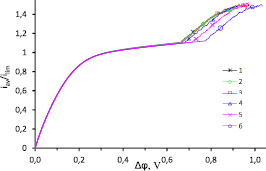
Рис. 2. а – ВАХ, рассчитанные для c0 = 1 моль/м3 при разных значениях Nc: 1 – 100; 2 – 10; 3 – 1; 4 – 0,1; 5 – 0,01; 6 – условие (7)
Таблица 1
Значения порогового СП Δφcr при различных значениях Nc
|
Nc |
Условие первого рода (6) |
Условие второго рода (7) |
||||
|
100 |
10 |
1 |
0,1 |
0,01 |
||
|
Δφcr, В |
0,662 |
0,664 |
0,664 |
0,675 |
0,714 |
0,775 |
Сформулированная задача решена методом конечных элементов с помощью пакета Comsol Multiphysics 5.1. Алгоритм решения описан в [3]. Уравнения реализованы с помощью следующих модулей Comsol: поля концентраций анионов и катионов – Transport of Diluted Species; поле электрического потенциала – Poisson Equation’s; уравнение Навье-Стокса – Laminar Flow. Для вычисления этих полей используется раздельный алгоритм решения (Segregated solver): каждый шаг по времени разделяется на подшаги, на первом из которых рассчитываются концентрации и потенциал электрического поля, на втором – компоненты скорости и давление. Каждый шаг итеративно выполняется до достижения заданной точности.
Для корректного решения в ДЭС использовалась неравномерная вычислительная сетка: плотность сетки увеличивалась в областях у АОМ и КОМ, для которых характерны большие значения градиента полей концентраций, потенциала и скорости.
Все вычисления выполнены с помощью процессора Intel Core i7-4930K CPU.
Результаты исследования и их обсуждение
Расчеты проведены для следующих значений параметров: межмембранное расстояние (ширина канала) H = 0,5 мм, длина канала L = 2 мм, средняя скорость вынужденного течения раствора V0 = 0,8 мм/с, входная концентрация раствора электролита c0 = 1 моль/м3, температура T = 298 K, плотность раствора электролита ρ0 = 1002 кг/м3, коэффициент динамической вязкости η = 0,8937·10-3 Па·с, коэффициент диффузии катионов и анионов, соответственно, D1 = 1,33·10-9 м2/с, D2 = 2,05·10-9 м2/с, отношения концентрации противоионов на границе с АОМ и КОМ к ее значению на входе в канал Na и Nc устанавливались равными 100; 10; 1; 0,1; 0,01.
Рассчитанные ВАХ приведены на рис. 2, кривые 1–5 рассчитаны с использованием условия первого рода (6), кривая 6 рассчитана с граничным условием второго рода (7). Из рис 2 видно, что все ВАХ имеют подобное поведение и отличаются пороговым СП перехода к неустойчивому режиму Рубинштейна-Зальцмана Δφcr (табл. 1).
При этом ВАХ для Nc = 100, 10 и 1 ВАХ малоразличимы; при Nc = 0,1 пороговое значение СП Δφсr немного больше, при Nc = 0,01 – еще больше. Пороговое значение СП Δφсr кривой 6 заметно больше остальных случаев. В этом случае отношение Nc зависит от приложенного СП и координаты y. Так, при Δφ = 0,8 В Nc колеблется от 0,0003 до 0,0018 вдоль поверхности мембраны, за исключением небольшой области у входа в канал.
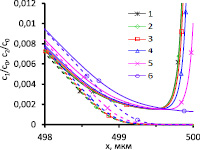 а)
а) 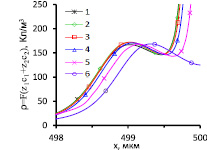 б)
б)
Рис. 3. а) – безразмерные концентрационные профили вблизи поверхности КОМ (сплошные линии – концентрации катионов, пунктирные линии – концентрации анионов) в сечении y = 1800 мкм, б) – плотность пространственного заряда в том же сечении. Расчет для c0 = 1 моль/м3 при СП Δφ = 0,65 В, и различных Nc: 1 – 100; 2 – 10; 3 – 1; 4 – 0,1; 5 – 0,01; 6 – условие (7)
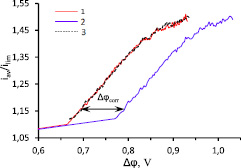
Рис. 4. Фрагмент ВАХ, рассчитанных для: 1 – условия первого типа (6) с Na = Nc = 1; 2 – условия второго типа (7); 3 – скорректированный расчет по условию (7)
В [14] на основе решения краевой задачи для уравнений НПП в одномерном случае установлено, что значение локальных максимумов плотности пространственного заряда с высокой точностью не зависит от граничной концентрации противоионов. Вычисления для Nc = 100; 10; 1; 0,1; 0,01 и для условия (7) показали, что значения локальных максимумов при Δφ = 0,65 В, меньшем чем Δφсr, отличаются не больше чем на 3 % (рис. 3). Тем не менее, пороговое напряжение перехода к неустойчивому режиму Рубинштейна-Зальцмана зависит от Nc, так как оно влияет на локализацию пространственного заряда: для Nc = 100, 10 и 1 они приблизительно совпадают, а для Na = Nc = 0,1 и 0,01 имеется небольшой сдвиг по направлению к мембране, а для условия (7) – значительный сдвиг (то есть максимум ОПЗ находится ближе к границе с условием прилипания, где вязкостные силы больше). Расстояние локализации ОПЗ от поверхности мембраны с ростом приложенного СП увеличивается и при некотором пороговом значении (зависящем от Nc) становится достаточным для того, чтобы действие поверхностных вязких сил не подавляло развитие ЭК.
а)
б)
в)
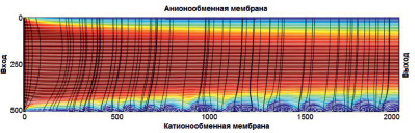
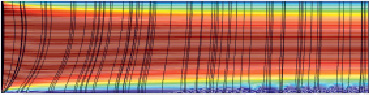
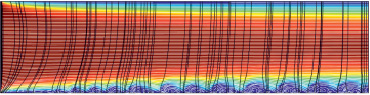
Рис. 5. Распределение концентрации катионов (показано различными цветами), линии течения раствора (белые линии), линии электрического тока (черные линии): а) расчет по условию первого рода (6) при Δφ = 0,8 В; б) расчет по условию второго рода (7) при Δφ = 0,8 В; в) расчет по условию (7) при Δφ + Δφcorr = 0,895 В
Таким образом, в случае применения условия первого типа (6) при Nc ≥ 1 величина Nc на результаты вычислений не влияет и для упрощения вычислений целесообразно принимать Nc = Nа = 1. Большей оптимизации вычислений можно добиться применением условия второго рода (7), так как ВАХ, рассчитанные с условием первого рода (6) и условием второго рода (7), в сверхпредельном состоянии обладают подобным поведением. Сдвинув сверхпредельную часть ВАХ расчета с условием (7) на корректирующий СП Δφcorr = 0,095 В, мы получили результат, очень близкий к результату расчета с условием первого типа (6) (рис. 4).
На рис. 5 показаны течения раствора электролита, рассчитанные по условию (6) при Δφ = 0,8 В, по условию (7) при Δφ = 0,8 В, и по условию (7) при Δφ + Δφcorr = 0,895 В.
Для оценки погрешности вычислений использовался следующий тест сходимости: на некоторой вычислительной сетке (состоящей из N1 элементов) проводились вычисления и рассчитывалась усредненная по времени безразмерная плотность тока при Δφ = 0,8 В (когда в канале уже развито электроконвективное вихревое течение), 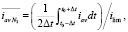
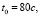
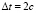 . Затем улучшается сетка (N2 элементов), еще раз проводятся вычисления и рассчитывается величина
. Затем улучшается сетка (N2 элементов), еще раз проводятся вычисления и рассчитывается величина 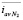 . Определяется относительная погрешность вычисления средней плотности тока
. Определяется относительная погрешность вычисления средней плотности тока 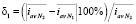 . Указанные действия выполнялись до тех пор, пока δm ≤ 0,4 %, где m – номер расчета. Условие остановки расчета с условием первого типа (6) было выполнено при Nm = 97249 и для условия второго типа (7) при Nm = 67289. Это связано с тем, что при использовании условия второго типа из рассмотрения исключается область с большим градиентом концентрации у поверхности мембраны. Отметим, что для условия второго типа (7) средний ток рассчитывался при СП Δφ + Δφcorr = 0,895 В. Применение условия второго типа (7) позволило получить решение той же точности, что и условие первого типа (6), сократив количество элементов сетки на 31 %.
. Указанные действия выполнялись до тех пор, пока δm ≤ 0,4 %, где m – номер расчета. Условие остановки расчета с условием первого типа (6) было выполнено при Nm = 97249 и для условия второго типа (7) при Nm = 67289. Это связано с тем, что при использовании условия второго типа из рассмотрения исключается область с большим градиентом концентрации у поверхности мембраны. Отметим, что для условия второго типа (7) средний ток рассчитывался при СП Δφ + Δφcorr = 0,895 В. Применение условия второго типа (7) позволило получить решение той же точности, что и условие первого типа (6), сократив количество элементов сетки на 31 %.
На рис. 6 приведены зависимость затрат времени на расчет одной секунды от величины СП Δφ для расчетов с условиями первого и второго родов. Видно, что в обоих случаях временные затраты становятся значительными при СП больше порогового Δφсr и увеличиваются с ростом СП. При этом временные затраты для условия второго рода (7) меньше, чем затраты для условия первого рода (6).
Учитывая эти особенности вычислений, предлагается следующий алгоритм численного решения модели:
1. Выполнить расчёт с условием первого рода до порогового скачка Δφcr 1.
2. Выполнить расчет с условием второго рода до требуемого значения плотности тока, определить Δφcr 2.
3. Определить корректирующий СП Δφcorr = Δφcr 2 – Δφcr 1.
4. Результаты расчета с условием второго типа рассматривать с учетом поправки Δφcorr.
Так как вычислительные затраты до порогового СП Δφcr малы (менее 1 % от полного времени расчета от 0 до 0,9 В), применение предложенного алгоритма позволяет сократить вычислительные затраты: время расчета по предложенному алгоритму от 0 до СП Δφk + Δφcorr = 0,995 В по сравнению со временем расчета по условию первого рода до Δφk = 0,9 В меньше на 45 % (см. табл. 2).
Таблица 2
Полное время расчета для условий первого и второго родов
|
Погрешность, δ |
Количество элементов сетки, N |
Время расчета от 0 до 90 с, ttot, ч |
|
|
Условие первого типа (6) |
0,4 % |
97249 |
85,5 |
|
Условие второго типа (7) |
0,4 % |
67289 |
46,2 |
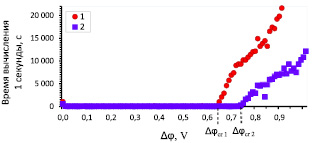
Рис. 6. Зависимость вычислительных затрат времени на одну секунду от величины СП. 1 – расчет с условием первого рода; 2 – с условием второго рода
Заключение
Анализ граничных условий первого и второго рода показал, что ВАХ для этих условий имеют подобное поведение и отличаются пороговым СП. При этом в случае применения условия первого рода (6) при Nc ≥ 1, величина Nc на результаты вычислений не влияет. Поэтому для упрощения вычислений целесообразно принимать Nc = 1. Большей оптимизации вычислений можно добиться применением условия второго рода (7), так как оно позволяет значительно сократить количество элементов вычислительной сетки и повысить производительность вычислений математической модели массопереноса в мембранных системах с учетом электроконвекции и вынужденного течения.
Библиографическая ссылка
Узденова А.М. МОДЕЛИРОВАНИЕ ЭЛЕКТРОКОНВЕКЦИИ В МЕМБРАННЫХ СИСТЕМАХ: АНАЛИЗ ГРАНИЧНЫХ УСЛОВИЙ У ПОВЕРХНОСТИ // Фундаментальные исследования. 2016. № 12-5. С. 1010-1017;URL: https://fundamental-research.ru/ru/article/view?id=41208 (дата обращения: 10.03.2026).
DOI: https://doi.org/10.17513/fr.41208



