Задачи линейного программирования транспортного типа широко распространены в практических исследованиях оптимизации различных экономических задач [1]. Однако существующие методы их решения нетривиальны и требуют специальной теоретической подготовки [1–3], как и вообще при решении любых других задач линейного программирования. В настоящее время существуют компьютерные программы, позволяющие решать подобные задачи с любым количеством переменных. Но для правильного использования этих программ и анализа найденного решения необходимо освоить хотя бы простейшие методы решения задач с малым числом переменных.
Авторам удалось построить простой универсальный метод решения задач линейного программирования с помощью исключения переменных в системе линейных неравенств, используя таблицы Гаусса [4, 5]. Данная работа демонстрирует применение этого метода к решению транспортных задач.
Решение транспортной задачи с правильным балансом
Пусть исходная таблица имеет вид:
|
bj ai |
10 |
12 |
8 |
|
17 |
3 х11 |
5 х12 |
2 х13 |
|
13 |
4 х21 |
1 х22 |
7 х23 |
где xij – объёмы перевозок от i-го поставщика к j-му потребителю, ai – запасы поставщиков, bj – запросы потребителей. Числа рядом с xij указывают стоимость cij перевозки единицы груза. Переменные xij должны удовлетворять следующим ограничениям:
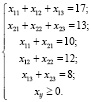 (1)
(1)
Приведём систему (1) к разрешённому виду, используя таблицы Жордана-Гаусса [2, 3].
В итоге решение системы (1) имеет вид:
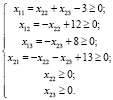 (2)
(2)
Целевая функция 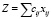 является суммой затрат на перевозку всех грузов и должна быть минимальна:
является суммой затрат на перевозку всех грузов и должна быть минимальна: 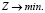
С учётом (2):
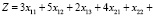
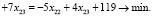 (3)
(3)
Как показано в [4], система неравенств, обеспечивающая Zmin, объединяет (2), (3) и выглядит следующим образом:
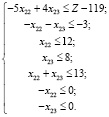 (4)
(4)
Исключаем переменные в системе (4) с помощью таблиц Гаусса, как в [4]:
Заметим, что в табл. 2 вычеркнуты автоматически выполняющиеся неравенства-следствия, например 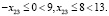
Таблица 1
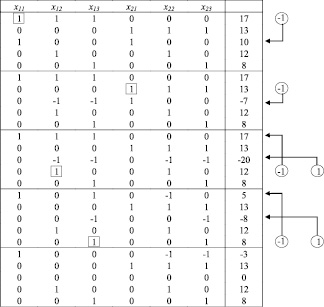
Таблица 2
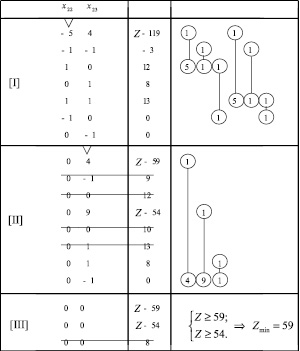
Подставляя Z = 59 в подтаблицу II, получим:
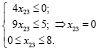 .
.
Подставляя Z = 59 и x23 = 0 в подтаблицу I, найдём:
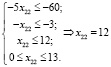 .
.
С учётом (2) окончательное решение данной транспортной задачи таково:
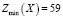 при
при 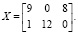
В общем случае т поставщиков и п потребителей (начало табл. 3) выглядит так:
Таблица 3
|
x11 |
x12 |
… |
x1n |
x21 |
x22 |
… |
x2n |
… |
xm1 |
xm2 |
… |
xmn |
|
|
1 |
1 |
… |
1 |
0 |
0 |
… |
0 |
… |
0 |
0 |
… |
0 |
a1 |
|
0 |
0 |
… |
0 |
1 |
1 |
… |
1 |
… |
0 |
0 |
… |
0 |
a2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
0 |
0 |
0 |
… |
0 |
… |
1 |
1 |
… |
1 |
am |
|
1 |
0 |
… |
0 |
1 |
0 |
… |
0 |
… |
1 |
0 |
… |
0 |
b1 |
|
0 |
1 |
… |
0 |
0 |
1 |
… |
0 |
… |
0 |
1 |
… |
0 |
b2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
1 |
0 |
0 |
… |
1 |
… |
0 |
0 |
… |
1 |
bn |
Нетрудно проверить, что в окончательной подтаблице табл. 3 первая строка заменится на:
|
1 |
0 |
… |
0 |
0 |
– 1 |
… |
– 1 |
… |
0 |
– 1 |
… |
– 1 |
a1 – (b2+…+bn), |
а строка с b1 будет состоять из одних нулей:
|
x11 |
x12 |
… |
x1n |
x21 |
x22 |
… |
x2n |
… |
xm1 |
xm2 |
… |
xmn |
|
|
1 |
0 |
… |
0 |
0 |
– 1 |
… |
– 1 |
… |
0 |
– 1 |
… |
– 1 |
a1 – (b2 +…+ bn) |
|
0 |
0 |
… |
0 |
1 |
1 |
… |
1 |
… |
0 |
0 |
… |
0 |
a2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
0 |
0 |
0 |
… |
0 |
… |
1 |
1 |
… |
1 |
am |
|
0 |
1 |
… |
0 |
0 |
1 |
… |
0 |
… |
0 |
1 |
… |
0 |
b2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
0 |
0 |
… |
1 |
0 |
0 |
… |
1 |
… |
0 |
0 |
… |
1 |
bn |
С помощью этой подтаблицы легко выписываются соотношения типа (2)–(4).
Решение транспортной задачи с неправильным балансом
Рассмотрим случай, когда запросы потребителей больше запасов поставщиков:
|
bj ai |
16 |
14 |
10 |
|
17 |
3 х11 |
5 х12 |
2 х13 |
|
13 |
4 х21 |
1 х22 |
7 х23 |
Ограничения на переменные таковы:
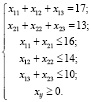 (5)
(5)
Выражая из равенств (5), например,
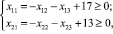 (6)
(6)
преобразуем целевую функцию
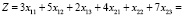
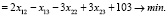 (7)
(7)
В итоге исходная система неравенств (5)–(7) рассматриваемой задачи выглядит так:
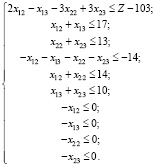 (8)
(8)
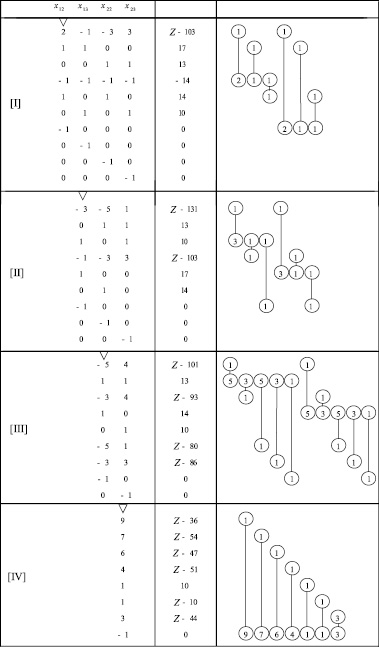
Далее, последовательно, исключая переменные x12, x13, x22, x23 (табл. 4), найдём решение задачи (8):
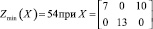 .
.
Столь же просто составляется система неравенств для транспортной задачи с ограничениями на пропускную способность типа
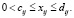
В этом случае к неравенствам вида (4), (8) добавляются ещё такие:
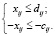
При этом неравенство – xij ≤ 0 следует откинуть, как выполняющееся автоматически.
Таблица 4
Библиографическая ссылка
Кравчук С.П., Кравчук И.С., Швед Е.В. РАЗРАБОТКА СПЕЦИАЛЬНОГО МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ СИСТЕМЫ ОПТИМИЗАЦИИ ЛОГИСТИЧЕСКИХ ЗАТРАТ НА ОСНОВЕ МЕТОДА НЕРАВЕНСТВ // Фундаментальные исследования. 2016. № 12-5. С. 998-1003;URL: https://fundamental-research.ru/ru/article/view?id=41206 (дата обращения: 15.02.2026).



