Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Рашоян Г.В. 1

---

1 Институт машиноведения им. А.А. Благонравова Российской академии наук (ИМАШ РАН)

В данной работе рассмотрим подход к структурному анализу и синтезу роботов параллельной структуры, основанный на математическом аппарате групп винтов и понятии взаимности винтов. В статье приведены результаты синтеза роботов параллельной структуры с различным числом степеней свободы, соответствующие различным группам винтов. Для этого на основе принципа статико-кинематической аналогии были указаны силовые винты, взаимные ортам осей неприводных кинематических пар соответствующей соединительной цепи. В свою очередь, одновременно определяются кинематические винты выходного звена робота, взаимные с силовыми винтами кинематических подцепей. Решения задач синтеза проиллюстрированы практическими решениями. Замкнутые группы винтов могут быть восьми видов. Наибольший интерес представляют собой трехчленные группы винтов, четырехчленные группы и шестичленные группы винтов. Трехчленные группы винтов соответствуют поступательно-направляющим механизмам, сферическим механизмам и плоским механизмам. Четырехчленная группа соответствует движению робота SCARA. Шестичленная группа включает все возможные движения. В статье представлены примеры механизмов, соответствующих данным группам.

Статья в формате PDF

0 KB

робот

параллельная структура

группа винтов

взаимный винт

1. Ганиев Р.Ф., Глазунов В.А. Манипуляционные механизмы параллельной структуры и их приложения в современной технике // ДАН. – 2014. – Т. 459. – № 4. – С. 1–4.

2. Глазунов В.А., Аракелян В., Брио С., Рашоян Г.В. Скоростные и силовые критерии близости к сингулярностям манипуляторов параллельной структуры // Проблемы машиностроения и надежности машин. – 2012. – № 3. – С. 10–17.

3. Глазунов В.А., Данилин П.О., Левин С.В., Тывес Л.И., Шалюхин К.А. Разработка механизмов параллельной структуры с кинематической и динамической развязкой // Проблемы машиностроения и надежности машин. – 2010. – № 2. – С. 23–32.

4. Глазунов В.А.,Колискор А.Ш., Крайнев А.Ф. Пространственные механизмы параллельной структуры. М.: Наука, 1991. 96 с.

5. Глазунов В.А., Чунихин А.Ю. Развитие механизмов параллельной структуры // Проблемы машиностроения и надежности машин. – 2014. – № 3. – С. 37–43.

6. Носова Н.Ю., Глазунов В.А., Палочкин С.В., Терехова А.Н. Синтез механизмов параллельной структуры с кинематической развязкой // Проблемы машиностроения и надежности машин. – 2014. – № 35. – С. 34–40.

7. Briot S., Glazunov V., Arakelian V. Investigation on the Effort Transmission in Planar Parallel Manipulators // Tr. ASME Journal of Mechanisms and Robotics. – 2013. – Vol. 5.

8. Glazunov V., Laryushkin P., Kheylo S. 3-DOF Translational and Rotational Parallel Manipulators // New Trends in Mechanism and Machine Science. Theory and Application in Engineering. Editors: F. Viadero and M. Ceccarelli. – Springer Dordrecht Heidelberg New York London. ISSN 2211-0984. 2012. – P. 199–207.

9. Rashoyan G.V., Lastochkin A.B., Glazunov V.A. Kinematic Analysis of a Spatial Parallel Structure Mechanism with a Circular Guide // Journal of Machinery Manufacture and Reliability. – 2015. – Vol. 44, № 7. – Р. 54–60. Allerton Press, Inc.

10. Glazunov V., Nosova N., Ceccarelli M. Kinematics of a 6 DOFs Manipulator with a Interchangeable Translation and Rotation Motions // Recent Advances in Mechanism Design for Robotics. Proceedings of the 3rd IFToMM Symposium on Mechanism Design for Robotics // Springer International Publishing Switzerland. ISSN 2211-0984. – 2015. – P. 407–416.

11. Kheylo S., Glazunov V. Kinematics, Dynamics, Control and Accuracy of Spherical Parallel Robot // Advances on Theory and Practice of Robots and Manipulators. Proceedings of ROMANSY 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. – Springer Cham Heidelberg New York Dordrecht London. ISSN 2211-0984. – 2014. – P. 133–140.

12. Kong X., Gosselin C., Type Synthesis of Parallel Mechanisms. – Springer, 2007.

13. Kozyrev A., Glazunov V. Finite Element Modeling and Analysis of an Izoglide -Type Parallel Manipulator to Determine its Rigidity/Stiffness // New Trends in Mechanism and Machines Sciences. – 2015. Springer. – Vol. 24. – P. 203–210.

14. Laryushkin P., Glazunov V., Demidov S. Singularity Analysis of 3-DOF Translational Parallel Manipulator // Advances on Theory and Practice of Robots and Manipulators. Proceedings of ROMANSY 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators. – Springer Cham Heidelberg New York Dordrecht London. ISSN 2211-0984. – 2014. – P. 47–54.

15. Merlet, J.-P., Parallel Robots (Second Edition). – Springer, 2006.

В данной работе рассматриваются различные подходы к структурному синтезу пространственных манипуляционных механизмов параллельной структуры, воспринимающих нагрузку подобно пространственным фермам. Один подход основан на аппарате замкнутых групп винтов. При этом все кинематические цепи налагают одинаковые связи.

Другой подход характеризуется тем, что кинематические цепи налагают разные связи, в совокупности обеспечивающие требуемые движения выходного звена. Приводятся примеры данных механизмов, рассматриваются их действующие модели.

В данной работе ставится задача создать алгоритм структурного синтеза многоподвижных одноконтурных кинематических цепей, основанный на применении алгебры Ли над группами движений, выраженной в виде замкнутых групп винтов. Нужно получить возможные структуры одноконтурных цепей с заданной подгруппой движения. Должна быть получена методика синтеза параллельных роботов, основанная на объединении групп кинематических винтов одноконтурных кинематических цепей по траекториям движений выходного звена.

Роботы параллельной структуры [1, 4, 5, 12, 15], обладающие уникальными свойствами в смысле грузоподъемности и быстродействия, могут быть описаны наиболее эффективным образом на основе теории винтов [3]. При этом каждой кинематической паре ставится в соответствие единичный винт – орт, расположенный вдоль оси. Для анализа силовых винтов, передаваемых на рабочий орган, следует определить винты, взаимные ортам осей неприводных пар.

Подобное рассмотрение применяется для анализа близости к особым положениям при выяснении, насколько то или иное положение соответствует предельным значениям углов давления [2, 8, 7]. При этом целесообразно уяснить, как сила передается на подвижную платформу, каков угол между линией силы и скоростью, которая будет иметь место при заторможенных приводах, всех, кроме одного.

Данная проблематика примыкает к проблеме построения роботов с кинематической развязкой, в которых каждый привод управляет движением лишь по одной координате [6]. На этой же основе строятся роботы параллельной структуры с различным числом степеней свободы и кинематических цепей [9–11, 13, 14].

В качестве алгоритма структурного синтеза может быть предложено применение модифицированной структурной формулы, которая предложена в 1991 г., для механизмов параллельной структуры [5]. Смысл этой формулы заключается в том, что твердое тело, двигаясь в пространстве, соответствующем той или иной замкнутой группе винтов, имеет l степеней свободы. l может быть равна шести, четырем, трем, двум и, как предельный случай, единице.

Каждая присоединяемая кинематическая цепь может налагать некоторые связи, число которых l – p, где p – количество подвижных кинематических пар.

В частном случае, когда l = 6, получаем структурную формулу

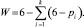
Здесь W – число степеней свободы; k – число кинематических цепей; pi – число одноподвижных кинематических пар.

В общем случае структурные формулы, соответствующие пространствам механизмов параллельной структуры, приобретают вид

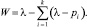
Здесь l – размерность пространства в котором функционирует механизм робота.

В данной работе приведем некоторые результаты, связанные с синтезом роботов параллельной структуры, соответствующих различным группам винтов. При этом всякий раз будут указаны силовые винты, взаимные ортам осей неприводных кинематических пар.

Рассмотрим применение групп винтов для построения роботов параллельной структуры. Вначале на этой основе представим поступательно-направляющий механизм (рис. 1). Каждая кинематическая цепь состоит из одной приводной поступательной пары, расположенной на основании, и, двух поступательных пар. Единичные винты, характеризующие положения осей указанных кинематических пар, имеют координаты (все винты имеют бесконечно большой параметр): K11 (0, 0, 0, 1, 0, 0), ..., K32 (0, 0, 0, k32x, k32y, 0), K33 (0, 0, 0, k33x, k33y, 0).

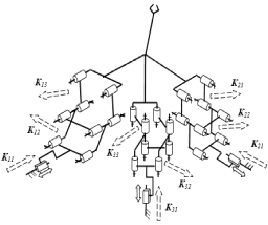
Рис. 1. Поступательно-направляющий механизм

Все три кинематические цепи налагают одинаковые связи. Силовые винты связей имеют координаты: Q1 (0, 0, 0, 1, 0, 0)...Q3 (0, 0, 0, 0, 0, 1). Кинематические винты выходного звена имеют координаты: Φ1 (0, 0, 0, 1, 0, 0), Φ2 (0, 0, 0, 0, 1, 0), Φ3 (0, 0, 0, 0, 0, 1).

Далее рассмотрим сферический механизм параллельной структуры (рис. 2). Каждая кинематическая цепь состоит из одной приводной вращательной пары и двух вращательных пар, причем оси всех пар пересекаются. Единичные винты, характеризующие положения кинематических пар: K11 (1, 0, 0, 0, 0, 0), K12 (k12x, k12y, k12z, 0, 0, 0), K13 (k13x, k13y, k13z, 0, 0, 0), K21 (0, 1, 0, 0, 0, 0), K22 (k22x, k22y, k22z, 0, 0, 0), K23 (k23x, k23y, k23z, 0, 0, 0), K31 (0, 0, 1, 0, 0, 0), K32 (k32x, k32y, k32z, 0, 0, 0), K33 (k33x, k33y, k33z, 0, 0, 0).

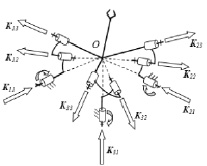
Рис. 2. Сферический механизм

Силовые винты связей имеют координаты: Q1 (1, 0, 0, 0, 0, 0), Q2 (0, 1, 0, 0, 0, 0), Q3 (0, 0, 1, 0, 0, 0). Кинематические винты выходного звена: Φ1 (1, 0, 0, 0, 0, 0), Φ2 (0, 1, 0, 0, 0, 0), Φ3 (0, 0, 1, 0, 0, 0).

Теперь рассмотрим плоский механизм параллельной структуры (рис. 3). В данном механизме две кинематические цепи содержат по три вращательные пары с параллельными осями, и одна кинематическая цепь содержит вращательную приводную пару и две поступательные пары. Единичные винты кинематических пар имеют координаты: K11 (0, 0, 1, 0, 0, 0), K12 (0, 0, 1, k12x, k12y, 0), K13 (0, 0, 1, k13x, k13y, 0), K21 (0, 0, 1, 0, 0, 0), K22 (0, 0, 1, k22x, k22y, 0), K23 (0, 0, 1, k23x, k23y, 0), K31 (0, 0, 1, 0, 0, 0), K32 (0, 0, 0, k32x, k32y, 0), K33(0, 0, 0, k33x, k33y, 0) .

Кинематические цепи налагают одинаковые связи. Силовые винты связей имеют координаты: Q1 (0, 0, 0, 1, 0, 0), Q2 (0, 0, 0, 0, 1, 0), Q3 (0, 0, 1, 0, 0, 0). Кинематические винты движения выходного звена: Φ1 (0, 0, 0, 1, 0, 0), Φ2 (0, 0, 0, 0, 1, 0), Φ3 (0, 0, 1, 0, 0, 0).

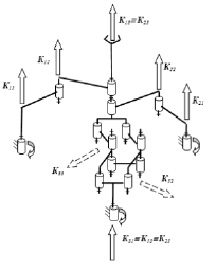
Рис. 3. Плоский механизм

Далее рассмотрим механизм параллельной структуры с четырьмя степенями свободы – три поступательных перемещения и вращение вокруг параллельных осей (рис. 4). Первая и вторая кинематические цепи состоят из одной приводной поступательной пары двух поступательных пар и вращательной пары. Третья кинематическая цепь содержит вращательную приводную пару, одну приводную поступательную пару, и две поступательные пары. Единичные винты кинематических пар имеют координаты: K11 (0, 0, 0, 1, 0, 0), K12 (0, 0, 0, 0, k12y, k12z), K13 (0, 0, 0, 0, k13y, k13z), K14 (0, 0, 1, 0, 0, 0), K21 (0, 0, 0, 0, 1, 0), K22 (0, 0, 0, k22x, 0, k22z), K23 (0, 0, 0, k23x, 0, k23z), K24 (0, 0, 1, 0, 0, 0), K31 (0, 0, 1, 0, 0, 0), K32 (0, 0, 0, 0, 0, 1), K33 (0, 0, 0, k33x, k33y, 0), K34 (0, 0, 0, k34x, k34y, 0).

Винты связей имеют координаты: Q1 (0, 0, 0, 1, 0, 0), Q2 (0, 0, 0, 0, 1, 0). Кинематические винты выходного: Φ1 (0, 0, 0, 1, 0, 0), Φ2 (0, 0, 0, 0, 1, 0), Φ3 (0, 0, 0, 0, 0, 1), Φ4 (0, 0, 1, 0, 0, 0).

Рассмотрим механизмы параллельной структуры с шестью степенями свободы и тремя соединительными кинематическими цепями 3 P-P-P-R-R-R (рис. 5). Каждая кинематическая цепь включает одну приводную поступательную пару, две поступательные пары, одну приводную вращательную пару и две неприводные вращательные пары. Оси всех вращательных пар пересекаются в точке O. Единичные винты кинематических пар: K11 (0, 0, 0, 1, 0, 0), K12 (0, 0, 0, 0, k12y, k12z), …, K34 (0, 0, 1, 0, 0, 0), К35 (k35x, k35y, k35z, 0, 0, 0), K36 (k36x, k36y, k36z, 0, 0, 0). Шесть кинематических винтов выходного звена: Φ1 (1, 0, 0, 0, 0, 0), Φ2 (0, 1, 0, 0, 0, 0), Φ3 (0, 0, 1, 0, 0, 0), Φ4 (0, 0, 0, 1, 0, 0), Φ5 (0, 0, 0, 0, 1, 0), Φ6 (0, 0, 0, 0, 0, 1).

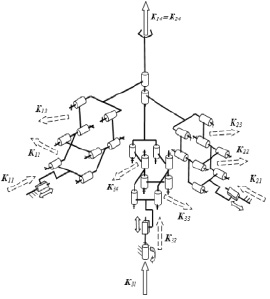
Рис. 4. Механизм с четырьмя степенями свободы

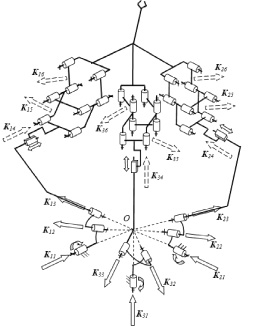
Рис. 5. Механизм с шестью степенями свободы

Далее рассмотрим механизм, в котором две кинематические цепи налагают по две связи (рис. 6), а третья кинематическая цепь связей не налагает. Первая и вторая кинематические цепи, как и в предыдущем случае. состоят из одной приводной вращательной пары (вращательный двигатель), расположенной на основании, одной промежуточной вращательной пары, расположенной с осью, параллельной оси вращательного привода и конечной цилиндрической двух подвижной пары (оси конечных цилиндрических пар двух цепей совпадают). Третья кинематическая цепь содержит одну вращательную приводную пару, установленную на основании, одну приводную поступательную пару (оси этих двух пар совпадают), а также два карданных шарнира, каждый из которых выполнен в виде двух вращательных кинематических пар с перпендикулярными пересекающимися осями, расположенными в горизонтальных плоскостях. 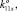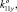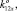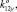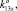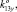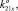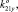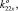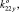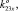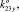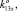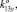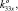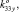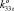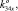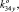Единичные винты, характеризующие положения осей указанных кинематических пар, имеют координаты: K11 (0, 0, 1, 0), K12 (0, 0, 1, 0), K13 (0, 0, 1, 0), K14 (0, 0, 0, 0, 0, 1), K21 (0, 0, 1, 0), K22 (0, 0, 1, 0), K23 (0, 0, 1, 0) = K13 (0, 0, 1, 0), K24 (0, 0, 0, 0, 0, 1) = K14 (0, 0, 0, 0, 0, 1), K31 (0, 0, 1, 0, 0, 0), K32 (0, 0, 0, 0, 0, 1), K33 (k33x, k33y, 0, ), K34 (k34x, k34y, 0, 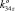), K35 (k35x, k35y, 0,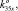 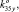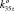), K36 (k36x, k36y, 0,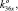 ). 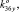Отметим, что k33x = k35x, k33y = k35y, k34x = k36x, k34y = k36y.

Винты K14, K24, K32 бесконечно большого параметра. Остальные винты нулевого параметра. Первая и вторая кинематические цепи налагают по две связи, которые могут считаться повторяющимися, они обусловливают число степеней свободы, равное четырем. Третья кинематическая цепь связей не налагает. Силовые винты связей, обусловленных кинематическими цепями, имеют координаты: Q1 (0, 0, 0, 1, 0, 0), Q2 (0, 0, 0, 0, 1, 0). Соответственно, все кинематические винты движения выходного звена вновь могут быть представлены как винты, взаимные указанным силовым винтам: Φ1 (0, 0, 0, 1, 0, 0), Φ2 (0, 0, 0, 0, 1, 0), Φ3 (0, 0, 0, 0, 0, 1), Φ4 (0, 0, 1, 0, 0, 0).

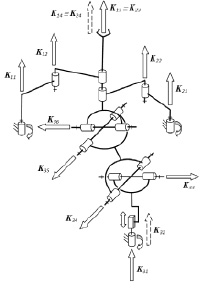
Рис. 6. Механизм с четырьмя степенями свободы и карданным валом

Рис. 7. Плоский механизм с тремя степенями свободы

Приведем примеры действующих моделей механизмов параллельной структуры. В Институте машиноведения им. А.А. Благонравова РАН были синтезированы плоские и пространственные системы (рис. 7, 8). В частности, был изготовлен плоский механизм с тремя степенями свободы (рис. 7) и тремя кинематическими цепями. Имеет место также сферический механизм (рис. 8) с кинематическими цепями, выполненными в виде дуг.

Рис. 8. Сферический механизм

Таким образом, на основании аппарата замкнутых групп винтов можно осуществить структурный синтез механизмов параллельной структуры.

Работа выполнена при поддержке Российского научного фонда, Соглашение № 16-19-001048.

Библиографическая ссылка