В настоящее время для изготовления значительной номенклатуры товаров широкого потребления используются детали в виде длинных тонкостенных труб диаметром 16…50 мм и толщинами стенок от 0,5 до 3 мм. Основными требованиями, предъявляемыми к таким трубам, являются низкая шероховатость (Ra 0,12 мкм… Ra 0,32 мкм), отклонения от круглости в пределах 0,1 мм при допуске на наружный диаметр трубы по 14 и более низким квалитетам точности.
Традиционные методы обработки длинных валов и тонкостенных труб сводятся к последовательному удалению припуска точением или наружным шлифованием с последующими отделочными методами для уменьшения высотных показателей шероховатости такими, как полирование, суперфиниширование и т.п. При этом в качестве исходных заготовок используются трубы в состоянии поставки прокатного производства, имеющие большие отклонения по наружному диаметру и по допуску круглости в пределах ±3 % от наружного диаметра трубы. Недостатками этих методов обработки являются высокая трудоемкость, низкая производительность, наличие нескольких последовательных операций, и высокая технологическая себестоимость [4]. Устранение имеющихся недостатков может быть решено на основе применения метода ротационного обкатывания полноконтактными роликами [2]. Этот метод применительно к тонкостенным трубам практически не применялся и по этой причине не исследован [3].
Ротационное обкатывание относится к методам обработки деталей поверхностным пластическим деформированием. Одним из определяющих факторов, оказывающих влияние на процесс деформирования, является площадь контакта, так как при одном и том же усилии, но при разных площадях контакта удельное давление может значительно отличаться [1]. Поэтому усилие деформирования может назначаться исходя из давления, которое необходимо обеспечить, и площади контакта, определяемой через геометрические параметры ролика, детали и их взаимного положения. В этой области различными авторами получен ряд зависимостей, которые предназначены для контакта деформирующих элементов шаровой, торовой или конической формы. Например, в работе [5] приводятся методика и результаты определения геометрических параметров и площади контакта при ППД наружных цилиндрических поверхностей вращения роликами конической формы (1). Сфера применения этой методики ограничена.
 [5]. (1)
[5]. (1)
Для подтверждения эффективности метода ротационного обкатывания тонкостенной трубы разработана расчетная схема обработки, показанная на рис. 1.
Деформирующие ролики установлены по отношению к оси детали на угол самозатягивания ω, соответствующий подаче. Зависимость угла самозатягивания и подачи можно определить по формуле
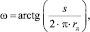 (2)
(2)
где s – подача головки на оборот; rd – наружный диаметр обрабатываемой тонкостенной трубы.
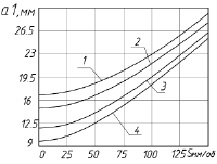
На рис. 2 показаны графики изменения величины угла установки деформирующих роликов от самоподачи.
Из представленных графиков видно, что с увеличением угла самозатягивания в пределах 0…45° подача изменяется в пределах вплоть до 100 мм/об. Такие величины подач на токарных станках отсутствуют. Поэтому при обработке ротационным обкатыванием можно использовать самоподачу.
Рассмотрим обкатывание трубы вогнутым роликом, образующая которого представляет дугу окружности радиуса Rop.
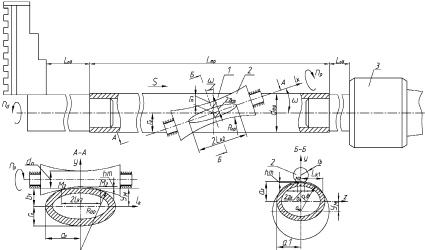
Рис. 1. Схема обработки тонкостенной трубы ротационным обкатыванием роликами с вогнутой образующей: 1 – обрабатываемая тонкостенная труба; 2 – деформирующий ролик; 3 – специальный задний центр; 4 – кулачок трехкулачкового патрона; 5 – вставка для центрирования трубы по оси совпадающей с осью вращения шпинделя станка и заднего центра
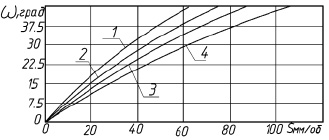
Рис. 2. Зависимости изменения угла самозатягивания от подачи при разных значениях радиусов обрабатываемой трубы: 1 – rd = 10 мм; 2 – rd = 12 мм; 3 – rd = 14 мм; 4 – rd = 17 мм
Деформирующие ролики в среднем сечении при обработке внедрены в обрабатываемую поверхность трубы на глубину hm, в результате чего происходит упругопластическая деформация поверхности трубы. В остальных сечениях ролика по его длине глубина внедрения в поверхность детали уменьшается и становится равной нулю в сечении ролика соответствующего началу и концу контакта.
Установим основные закономерности формирования контактной зоны между поверхностями ролика и детали. С точки зрения технологичности изготовления образующая рабочей поверхности обжимающего ролика должна быть дугой окружности с радиусом Rоp.
В этом случае изменение радиуса деформирующего ролика с вогнутой образующей по длине контакта можно вычислить из выражения
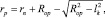 (3)
(3)
где rn – начальный радиус ролика в средней части контакта (начальный радиус); Rор – радиус образующей ролика; lk – текущая координата длины контакта.
Произведем сечение деформирующего ролика и детали двумя плоскостями перпендикулярными оси ролика (рис. 1).
При установке обжимающего ролика на угол самозатягивания ω в сечении на поверхности трубы как плоскостью Б-Б, так и плоскостью А-А (рис. 1) образуется эллипс. Малая полуось b1 в сечении плоскостью Б-Б равна
b1 = rd, (4)
большая полуось эллипса a1 в этом же сечении равна
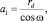 (5)
(5)
где rd – радиус обрабатываемой трубы; ω – угол самозатягивания; hm – максимальная глубина внедрения ролика в поверхность трубы.
Аналогично малая и большая полуоси эллипса образуемого в сечении А-А будут равны
b2 = rd; (6)
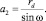 (7)
(7)
Как видно из представленных на рис. 3 графиков в сечении А-А большая полуось эллипса быстро уменьшается в зависимости от подачи, а в сечении Б-Б, наоборот, увеличивается.
Определим длину, ширину контакта и закон изменения полуширины контакта по его длине. Очевидно, что форма контакта между деформирующим роликом и трубой тоже будет представлять собой эллипс, а ее размеры будут зависеть от полуосей эллипсов, образуемых в сечениях Б-Б и А-А.
Для упрощения решения задачи заменим дугу эллипса дугой эквивалентной окружности с радиусом Rop. Этот эквивалентный радиус будет также представлять радиус образующей выпуклого деформирующего ролика. Расчетная схема для определения радиуса эквивалентной окружности и длины контакта между деформирующим роликом и поверхностью трубы представлена на рис. 4.
Предположим, что длина и ширина контакта между роликом и обрабатываемой трубой будут пропорциональны длинам больших полуосей с коэффициентом меньшим единицы.
Для определения полудлины контакта между роликом и трубой в каждом из сечений можно записать следующее выражение
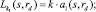 (8)
(8)
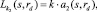 (9)
(9)
где k – упомянутый выше коэффициент пропорциональности меньший единицы; а1 – малая полуось эллипса, образуемая в сечении Б-Б, а2 – большая полуось эллипса, образуемая в сечении А-А.
Эти значения полуосей контактов являются одновременно координатами у1 и у2 точек М1 и M2 пересечения эллипсов, образуемых в сечениях тонкостенной трубы с эквивалентной окружностью.
Уравнения эллипсов в сечениях трубы плоскостями Б-Б и А-А можно записать в следующем виде:
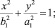
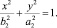 (10)
(10)
Из этих уравнений находим значение координат х1 и х2 точек М1 и М2 пересечения эллипсов в сечениях Б-Б и А-А с эквивалентными окружностями:
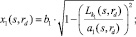 (11)
(11)
 а
а 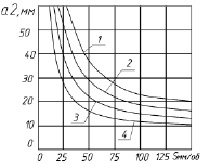 б
б
Рис 3. Изменение больших полуосей эллипсов, образуемых в сечениях ролика и детали плоскостями Б-Б (а) и А-А (б) в зависимости от подачи при разных диаметрах тонкостенной трубы: 1 – rd = 10 мм; 2 – rd = 12 мм; 3 – rd = 14 мм; 4 – rd = 17 мм
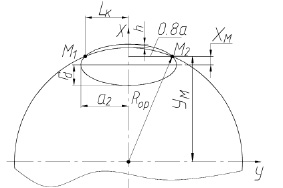
Рис. 4. Расчетная схема для определения радиуса эквивалентной окружности и полудлины контакта Lk в сечениях ролика и трубы плоскостями А-А и Б-Б
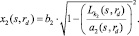 (12)
(12)
Из анализа расчетной схемы на рис. 4 находим значения ординат точек М1 и М2 пересечения эллипса с эквивалентной окружностью
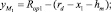 (13)
(13)
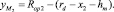 (14)
(14)
Из уравнений (13)–(14) находим радиусы эквивалентных окружностей
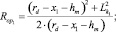 (15)
(15)
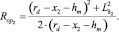 (16)
(16)
При пересечении двух окружностей, одна из которых внедрена в другую на величину hm, полуширина контакта в среднем сечении ролика может быть вычислена по формуле
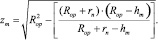 (17)
(17)
Тогда уравнение эллипса, определяющего контактную зону между роликом и обрабатываемой поверхностью, можно записать в виде
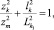 (18)
(18)
откуда получаем уравнение эллипса, определяющего закон изменения полуширины контакта между поверхностями ролика и трубы в виде
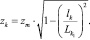 (19)
(19)
Для определения площади контакта, используя уравнение (19), можно написать следующую формулу:
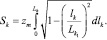 (20)
(20)
Полученные зависимости позволяют определять требуемый угол самозатягивания и длину контакта при пересечении деформирующего ролика с поверхностью обрабатываемой заготовки, что в свою очередь позволяет достигать полного перекрытия винтовых следов от деформирующих роликов.
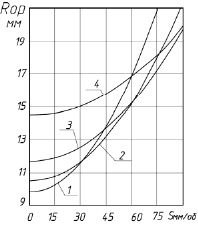
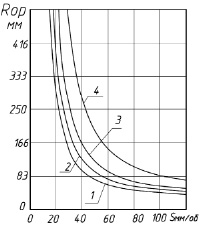
а б
Рис. 5. Изменение радиусов эквивалентных окружностей, образуемых в сечениях ролика и детали плоскостями Б-Б (а) и А-А (б), в зависимости от подачи при разных диаметрах тонкостенной трубы: 1 – rd = 10 мм; 2 – rd = 12 мм; 3 – rd = 14 мм; 4 – rd = 17 мм
Также результаты позволяют определить площадь контакта и рассчитать величину силы деформирования, необходимую для обработки поверхностным пластическим деформированием и одновременно не приводящую к возникновению остаточной деформации стенки тонкостенной трубы, через распределенные контактные напряжения.
Библиографическая ссылка
Лаврентьев А.М. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ КОНТАКТНОЙ ЗОНЫ ПРИ РОТАЦИОННОМ ОБКАТЫВАНИИ РОЛИКОМ С ВОГНУТОЙ ОБРАЗУЮЩЕЙ // Фундаментальные исследования. 2016. № 12-4. С. 742-747;URL: https://fundamental-research.ru/ru/article/view?id=41162 (дата обращения: 16.02.2026).



