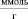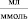ИССЛЕДОВАНИЕ СОРБЦИИ ИОНОВ МЕДИ (II) ПРИРОДНЫМ СОРБЕНТОМ

Пимнева Л.А. 1 Лебедева А.А. 1

1 Тюменский индустриальный университет

Представлены результаты исследований сорбции ионов меди из водных растворов каолинитовой глиной обработанным раствором NaCl.Определена структурная формула каолинитовой глины. Определены значения предельной статической сорбционной емкости каолинитовой глины, которая составляет 5,0 ммоль/г. Вычислены коэффициенты распределения ионов меди, значения которых уменьшаются с увеличением концентрации исходного раствора. Исследовано равновесие обмена ионов меди на каолинитовой глине методом построения изотерм при изменении температуры процесса от 298 К до 333 К. Описание сорбционного процесса проводилось моделями Ленгмюра, Фрейндлиха и Темкина. Расчеты показали, что наилучшим образом данные по сорбции описываются моделью Ленгмюра. Установлена природа взаимодействия ионов меди с каолинитовой глиной в солевой форме. Полученные значения энергии Гиббса имеют отрицательный знак – 10,25 (298 К); – 12,01 (313 К); – 14,71 (333 К) кДж/моль, что соответствует устойчивому закреплению ионов меди на поверхности каолинитовой глины.

Статья в формате PDF

0 KB

природный сорбент

сорбция

ионы меди

изотермы сорбции

количественные характеристики процесса сорбции

1. Бетехтин А.Г. Курс минералогии – учебное пособие / А.Г. Бетехтин. – М.: КДУ, 2007. – 720 С.

2. Воюцкий С.С. Курс коллоидной химии. / С.С. Воюцкий. – М.: Химия, 1976. – 512 с.

3. Иванова Е.С. Структура и сорбционные свойства Н-формы глины Луковского месторождения Псковской области / Е.С. Иванова, Ю.Ю. Гавриловская, В.Н. Пак // Сорбционные и хроматографические процессы. – 2014. – Т. 14. – Вып. 2. – С. 254–259.

4. Калюкова Е.Н. Адсорбция катионов марганца и железа природными сорбентами / Е.Н. Калюкова, В.Т. Письменко, Н.Н. Иванская // Сорбционные и хроматографические процессы. – 2010. – Т. 10. – Вып. 2. – С. 194–200.

5. Николаев Е.Н. Кинетика ионного обмена на смолах / Е.Н. Николаев //Кинетика и динамика физической адсорбции. – М., 1973. – С. 32–37.

6. Николаев Н.И. Кинетика сорбции ионов меди комплексующими карбоксильными ионообменниками / Н.И. Николаев, А.А. Эфендиев, А.Т. Шахтинская // ДАН СССР – 1977. – Т. 235, № 2. – С. 642–646.

7. Пимнева Л.А. Изотермы сорбции ионов бария, меди и иттрия накарбоксильном катионите КБ-4пх2 / Л.А. Пимнева, Е.Л. Нестерова // Современные наукоемкие технологии. – 2008. – № 4. – С. 15–20.

8. Танабе К. Твердые кислоты и основания. – М.: Мир, 1976. – 306 с.

9. Хурамшина И.З. Сорбционная доочистка медьсодержащих водных растворов / И.З. Хурамшин, А.Ф. Никифоров // Экология и промышленность России. – июнь 2013. – С. 29–31.

10. Шварценбах Г. Комплексометрическое титрование / Г. Шварценбах, Г. Флашка – М.: Химия, 1970. – 360 с.

В настоящее время серьезной проблемой является загрязнение природных вод промышленными стоками, что ухудшает экологическую обстановку. Сточные воды, как правило, представляют собой сложные гетерогенные системы, содержащие неорганические и органические вещества, находящиеся в растворенном, коллоидном и нерастворенном состояниях. Основной вклад в загрязнение вносят гальванические и травильные производства. Эти производства требуют большого количества воды [5] для промывки обрабатываемых деталей, в результате чего происходит сброс большого количества отходов [6]. В связи с этим ведется поиск эффективных и экологически выгодных методов очистки сточных вод от цветных и тяжелых металлов.

Каолинит как природный минерал известен давно [1], является главным составляющим всех глин. Основа – это водные алюмосиликаты Al₄[Si₄O₁₀][OH]₈ с небольшими примесями железа (III), магния, кальция, натрия, калия. Для каолинита характерна триклинная сингония а₀ = 5,14; b₀ = 8,90; c₀ = 14,45; β = 100 °12’ [1]. Цвет минерала от белого, нередко с желтым, буроватым, красноватым, иногда зеленоватым или голубоватым оттенком. Твердость около 1 по десятибалльной шкале. Удельный вес в пределах 2,58–2,60 г/см3. Каолинит не плавится, устойчив к HCl и HNO3, но при нагревании с H2SO4 легко разлагается. При нагревании выше 300 ° каолинит полностью разрушается.

В последнее время глинистые минералы являются объектами многочисленных исследований [3–6, 9] с целью использования их как местного сырья для решения региональных экологических проблем. Это связано с очисткой сточных вод различного происхождения. Использование местного сырья для извлечения цветных металлов из сточных вод характеризуется высокой экономичностью и малым расходом сорбента.

Цель – настоящей работы результаты исследований структуры и сорбционных свойств каолинитовой глины, которая может быть применена для очистки сточных вод от ионов меди.

Материалы и методы исследования

Природный сорбент каолинитовая глина представляет собой легкий порошок белого цвета с размерами частиц 2–20 мкм и насыпной плотностью 0,3 г/см3. На рис. 1 представлена СЭМ-микрофотография образца сорбента, полученная на сканирующем электронном микроскопе. По полученным данным основными его компонентами являются оксиды в количествах, представленных в табл. 1.

Атомное отношение алюминия к кремнию по представленным данным составляет ~ 1/2,4 и это соответствует максимальному числу и силе кислотных центров поверхности алюмосиликатного каркаса каолинитовой глины [8]. Активными центрами являются подвижные ионы Na⁺ и K⁺, принимающие участие в обмене на ионы тяжелых металлов.

Минералогический состав каолинитовой глины определяли рентгенофазовым анализом. На рис. 2 представлена рентгенограмма, снятая на дифрактометре «ДРОН-7» с медным анодом (λ = 1,5406 A).

Результаты рентгенофазового анализа дают дополнительные основания для предположения о высокой подвижности и обменной способности катионов Na⁺ и K⁺, удерживаемых на поверхности каолинитовой глины.

Изучение сорбции ионов меди (II) на каолинитовой глине проводили в статических условиях из сульфатных растворов с концентрациями от 0,01 до 0,24 ммоль/мл. Сорбент в солевой форме (обработанный раствором NaCl) в количестве 1 г заливали 50 мл растворами. Контакт сорбента с раствором продолжался до установления равновесия в течение 7 суток. Затем сорбент и раствор отделяли и анализировали на содержание ионов меди и измеряли рН среды. Концентрацию катионов меди в растворе определяли комплексонометрическим титрованием с трилоном Б в присутствии индикатора ПАН [10].

Результаты исследования и их обсуждение

По полученным экспериментальным данным рассчитали статическую емкость каолинитовой глины в солевой форме по меди (II) (ммоль/г)

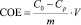pimn01.wmf ,

коэффициент распределения Кd, мл/г

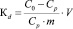pimn02.wmf , мл/г,

и степень сорбции α ( %)

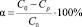pimn03.wmf ,

где C0 – концентрация меди в исходном растворе, ммоль/мл; Cp – равновесная (остаточная) концентрация извлекаемого иона в растворе, ммоль/мл; V – объем раствора, мл; m – масса сорбента, г. Результаты расчетов представлены в табл. 2.

Таблица 1

Содержание компонентов в составе каолинитовой глины

Содержание	SiO₂	Al₂O₃	Na₂O	K₂O	CaO	Fe₂O₃
% мас.	43,98	18,73	0,96	0,80	0,06	6,32
Число молей	0,732	0,180	0,015	0,007	0,009	0,057

pimnev1.tif

Рис. 1. СЭМ-микрофотография каолинита

pimnev2.tif

Рис. 2. Рентгенограмма образца каолинитовой глины

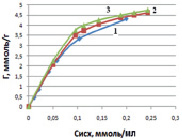
pimnev3.tif

Рис. 3. Зависимость величины сорбции ионов меди на модифицированной солевой форме каолинитовой глины при температурах, К: 298 (1); 313 (2); 333 (3)

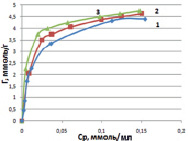
pimnev4.tif

Рис. 4. Изотермы сорбции ионов меди на каолинитовой глине в солевой форме (Na) при температурах, К: 298 (1), 313 (2), 333 (3)

Таблица 2

Коэффициент распределения, степень сорбции и статическая обменная емкость каолинитовой глины при извлечении ионов меди (II) из растворов при температуре 298 К

C_o, ммоль/мл	0,01	0,02	0,04	0,06	0,10	0,20	0,24
C_p, ммоль/мл	0,0025	0,0040	0,0065	0,0120	0,0365	0,1130	0,1545
К_d, мл/г	510,00	340,50	265,38	189,58	91,78	38,27	28,48
α, %	99,65	93,33	87,80	79,13	64,73	43,36	36,29
СОЕ, ммоль/г	0,45	0,85	1,73	2,28	3,35	4,33	4,40

Модифицированная каолинитовая глина, обработанная раствором NaCl, изменяет физико-химические свойства. При переводе природной формы каолинитовой глины в солевую форму происходит значительное увеличение положительного заряда поверхности. Последующие эксперименты показали, что выявленные изменения физико-химических свойств каолинитовой глины позволяют резко увеличить эффективность сорбции ионов меди на поверхности. На рис. 3 видно, что количество поглощенных ионов меди закономерно увеличивается с ростом концентрации в исходном растворе.

Более полную характеристику равновесия процесса сорбции можно получить с помощью изотерм. Вид изотерм показывает степень сродства сорбируемых ионов к сорбенту. Изотерма сорбции позволяет определить максимальную обменную емкость сорбента и рассчитать некоторые энергетические характеристики процесса. На изотермах сорбции, приведенных на рис. 4, виден резкий подъем в области малых равновесных концентраций меди. На этом отрезке наблюдается линейная зависимость количества сорбированных ионов меди от равновесной концентрации в растворе (отрезок Генри).

Для описания сорбционного процесса было использовано несколько моделей:

Ленгмюра:

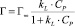
pimn04.wmf

или в линейной форме

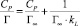
pimn05.wmf

где Г – количество сорбированной меди и Г∞ – величина предельной сорбции (ммоль/г), Cp – равновесная концентрация ионов меди в растворе (ммоль/мл), kL – концентрационная константа сорбционного равновесия, характеризующая интенсивность процесса сорбции, мл/ммоль;

Фрейндлиха:

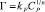
pimn06.wmf

или в логарифмической форме

pimn07.wmf

где kF и n – константы Фрейндлиха;

Темкина:

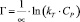
pimn08.wmf

или

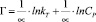
pimn09.wmf

где kT и ∞ – константы Темкина.

Модель изотермы Ленгмюра основана на том, что на поверхности катионита образуется мономолекулярный сорбционный слой и все активные места обладают равной энергией и энтальпией сорбции [2]. Модель Фрейндлиха используется для описания сорбции на гетерогенной поверхности [2]. Относительную сорбционную способность отражает константа kF, а интенсивность сорбционного процесса и распределение активных центров характеризует константа n. Если n = 1, то все сорбционные центры в сорбенте будут эквивалентны, при n > 1 энергия связи между сорбентом и сорбируемым ионом уменьшается по мере заполнения поверхности, а при n < 1 энергия связей возрастает. В этом случае в первую очередь происходит заполнение активных сорбционных положений с наименьшей энергией, что сопровождается непрерывным изменением энергии сорбции [7]. Энергия сорбции в изотерме Фрейндлиха находится в логарифмической зависимости от степени заполнения поверхности, в отличие от модели Темкина, в которой данная зависимость линейна.

Линейная обработка изотерм сорбции ионов меди из водных растворов на Na+ – форме каолинитовой глины представлены в табл. 3.

Результаты табл. 3 показывают, что наилучшим образом экспериментальные данные описываются моделью Ленгмюра. Полученные результаты подтверждают, что при сорбции ионов меди на солевой форме каолинитовой глине предельная сорбция Г∞ равна 5,0 ммоль/г, а константа сорбционного равновесия К равная 67,0 мл/ммоль (298 К), которая характеризует энергию взаимодействия ионов меди с поверхностью сорбента.

Значение константы n в уравнении Фрейндлиха больше 1, что свидетельствует о благоприятных условиях связанных с уменьшением энергии связи сорбент – сорбат по мере заполнения поверхности. Значение константы kF подтверждает легкость перехода сорбируемых ионов меди из раствора в фазу сорбента.

Таблица 3

Обработка изотерм сорбции ионов меди (II) по моделям

Т, К	Ленгмюра					Фрейндлиха			Темкина
Т, К			,	К,	Коэффициент корреляции	lgkF	1/n	Коэффициент корреляции	lgkT	1/α	Коэффициент корре-ляции
298	0,003	0,201	5,00	67,00	0,999	0,916	0,286	0,985	6,099	1,964	0,991
313	0,002	0,202	4,95	101,0	0,999	0,790	0,150	0,998	5,814	1,446	0,999
333	0,001	0,203	4,93	203,0	0,999	0,768	0,112	0,998	5,657	1,123	0,995

Свободную энергию Гиббса, кДж/моль, рассчитали по формуле

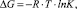
pimn15.wmf

где R – универсальная газовая постоянная, равная 8,314 Дж/моль•К; Т – температура, К; К – константа адсорбционного равновесия. Полученные значения энергии Гиббса имеют отрицательный знак – 10,25 (298 К); – 12,01 (313 К); – 14,71 (333 К) кДж/моль, что соответствует устойчивому закреплению ионов меди на поверхности каолинитовой глины.

Заключение

На основании приведенных исследований и полученных результатов можно сделать следующие выводы:

Изотермы сорбции ионов меди хорошо описываются различными моделями сорбции.

Определены значения предельной статической сорбционной емкости каолинитовой глины, которая составляет 5,0 ммоль/г, вычислены коэффициенты распределения, значения которых уменьшаются с увеличением концентрации ионов меди в растворе.

Рассчитаны значения энергии Гиббса 10,25 (298 К); 12,01 (313 К); 14,71 (333 К) кДж/моль.

Каолинитовая глина, переведенная в солевую форму, представляет собой перспективный природный сорбент для извлечения ионов меди из водных растворов.

Библиографическая ссылка

Пимнева Л.А., Лебедева А.А. ИССЛЕДОВАНИЕ СОРБЦИИ ИОНОВ МЕДИ (II) ПРИРОДНЫМ СОРБЕНТОМ // Фундаментальные исследования. 2016. № 12-2. С. 329-333;
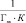
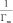
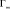URL: https://fundamental-research.ru/ru/article/view?id=41092 (дата обращения: 16.03.2025).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

«Современные проблемы науки и образования» список ВАК ИФ РИНЦ = 1,006

«Фундаментальные исследования» список ВАК ИФ РИНЦ = 1,674

«Современные наукоемкие технологии» список ВАК ИФ РИНЦ = 0,940

«Успехи современного естествознания» список ВАК ИФ РИНЦ = 0,775

«Международный журнал прикладных и фундаментальных исследований» ИФ РИНЦ = 0,593

«Международный журнал экспериментального образования» ИФ РИНЦ = 0,425

«Научное Обозрение. Биологические Науки» ИФ РИНЦ = 0,400

«Научное Обозрение. Медицинские Науки» ИФ РИНЦ = 0,801

«Научное Обозрение. Экономические Науки» ИФ РИНЦ = 0,871

«Научное Обозрение. Педагогические Науки» ИФ РИНЦ = 0,733