Под электромагнитным полем понимают особый вид материи, характеризующийся совокупностью взаимно связанных и взаимно обусловливающих друг друга электрического и магнитного полей [1].
Бегущее электромагнитное поле используется во многих электрических машинах и электромагнитных устройствах. При воздействии этого поля на проводящую среду в ней индуцируются токи и возникает тяговое усилие, направленное по направлению движения бегущего поля. На использовании электромагнитного поля основан принцип действия электрических машин как вращательного, так и возвратно-поступательного действия.
В Пермском национальном исследовательском политехническом университете (ПНИПУ) в течение ряда лет проводились инициативные научно-исследовательские работы по созданию и разработке вентильных линейных двигателей возвратно-поступательного движения с постоянными магнитами. Результаты этих исследований легли в основу проекта, выполненного авторами настоящей статьи в рамках работ по Постановлению Правительства РФ № 218 (договор № 02.G25.310068 от 23.05.2013 г.). В результате создан опытный образец цилиндрического линейного вентильного двигателя возвратно поступательного движения (ЦЛВД). Разработанный образец ЦЛВД предназначен для создания электропривода нового поколения для нефтедобычи как на существующих средне- и низкодебитных скважинах, так и для сверхглубоких скважин. ЦЛВД опускается в скважину и получает питание с помощью плоского армированного кабеля от электронного коммутатора, расположенного на поверхности земли рядом с устьем скважины. ЦЛВД в скважине создаёт возвратно-поступательное движение плунжерного насоса при управлении преобразователя от микропроцессорной системы, которая осуществляет необходимое число качаний и длину хода плунжера [4].
На основе разработанного ЦЛВД авторы статьи предполагают создать нефтяное оборудование нового поколения – погружной бесштанговый электронасосный агрегат возвратно-поступательного действия (ПБЭНА) с числовым программным управлением, который предназначен для замены традиционных станков-качалок, имеющих сегодня целый ряд принципиальных недостатков и не удовлетворяют требованиям перспектив развития нефтедобывающей отрасли. Например, глубина спуска плунжерного насоса станков-качалок не должна превышать 2000 метров из-за возможности обрыва штанг.
Создание ПБЭНА, позволяющего устранить недостатки традиционных станков-качалок (например, он может использоваться для скважин глубиной от 2000 м и более, выгодно и удобно добывать нефть в глубоких, наклонных, горизонтальных скважинах, а также малодебитных скважинах, на отмелях и морских нефтепромыслах), поэтому создание ЦЛВД является весьма важной научной и технической задачей, от решения которой зависит эффективность откачки пластовой жидкости на нефтепромыслах. В результате использования электропривода на основе ЦЛВД становится возможным дополнительно решить столетнюю сопутствующую проблему по клинообразному износу труб и штанг на станках-качалках, что серьезно осложняет ситуацию с нефтедобычей во всем мире. Кроме того, улучшится добыча «сложной» нефти.
Разработка ЦЛВД потребовала проведения достаточно глубоких научных исследований, создания опытных образцов и привела к необходимости разработки принципиально новых конструкций электропривода и созданию соответствующих научно обоснованных методик.
В настоящей статье рассматривается расчет электромагнитного поля, который использовался при разработке электропривода нового поколения на основе ЦЛВД для добычи нефти.
Расчет электромагнитного поля
В большинстве практических случаев решение конкретных задач расчета электромагнитного поля удобнее производить с помощью векторного потенциала магнитного поля 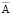 и скалярного потенциала электрического поля j.
и скалярного потенциала электрического поля j.
Эти потенциалы полностью характеризуют электромагнитное поле и после их определения расчет значений магнитной индукции 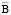 , напряженности электрического поля
, напряженности электрического поля 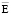 , напряженности магнитного поля
, напряженности магнитного поля 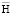 и плотности индуцированного тока
и плотности индуцированного тока 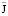 во всех точках среды не представляет особых трудностей.
во всех точках среды не представляет особых трудностей.
В настоящее время универсальная система дифференциальных уравнений для расчёта поля с помощью потенциалов 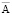 и j в электропроводящих средах отсутствует. Такое положение в значительной степени объясняется неоднозначностью понятия самого векторного потенциала. Действительно, магнитное поле в каждой точке среды полностью определяется векторами
и j в электропроводящих средах отсутствует. Такое положение в значительной степени объясняется неоднозначностью понятия самого векторного потенциала. Действительно, магнитное поле в каждой точке среды полностью определяется векторами 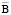 и
и 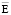 , которые могут быть определены бесчисленным множеством взаимосвязанных значений векторного и скалярного потенциалов.
, которые могут быть определены бесчисленным множеством взаимосвязанных значений векторного и скалярного потенциалов.
Поэтому сложность записи системы дифференциальных уравнений и трудоёмкость их решения в большей степени зависят от выбора калибровки или нормировки потенциалов, связывающих векторный и скалярный потенциалы. Удачный выбор калибровки позволяет получить достаточно простое уравнение для решения конкретного класса задач. Неудачный выбор, наоборот, может и чрезвычайно усложнить расчёт поля или привести вообще к неразрешимости задачи [2, 5].
Расчет осуществляется на базе основных уравнений электромагнитного поля [7].
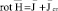 , (1)
, (1)
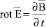 , (2)
, (2)
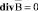 , (3)
, (3)
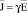 , (4)
, (4)
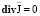 , (5)
, (5)
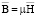 (6)
(6)
где J – плотность индуцированного в проводящей среде тока;
Jст – плотность стороннего тока, который создает электромагнитное поле;
μ – абсолютная магнитная проницаемость среды.
Реальные величины 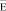 и
и 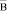 полностью определяют электромагнитное поле в проводящей среде. Для их нахождения очень часто используют векторный потенциал электромагнитного поля
полностью определяют электромагнитное поле в проводящей среде. Для их нахождения очень часто используют векторный потенциал электромагнитного поля  . Векторный потенциал это некоторая вспомогательная функция, с помощью которой очень часто бывает значительно проще определить основные величины, характеризующие электромагнитное поле. Обычно векторный потенциал подчиняют известному условию:
. Векторный потенциал это некоторая вспомогательная функция, с помощью которой очень часто бывает значительно проще определить основные величины, характеризующие электромагнитное поле. Обычно векторный потенциал подчиняют известному условию:
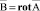 , (7)
, (7)
это уравнение не противоречит условию (3)
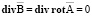 ,
,
так как дивергенция любого ротора равна нулю. Второе уравнение Максвелла (2) с учетом (7) можно записать в следующем виде:
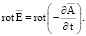 (8)
(8)
Так как левые и правые части уравнения (8) определяются операцией rot, то можно записать:
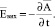 (9)
(9)
Данное выражение отражает вихревой характер напряженности электрического поля, которая возникает за счет изменения магнитного потока во времени. В общем случае напряженность электрического поля может иметь и потенциальную составляющую 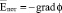 [3]. В этом выражении j скалярный потенциал электромагнитного поля, а общая напряженность электрического поля в проводящей среде равна вихревой и потенциальной составляющей
[3]. В этом выражении j скалярный потенциал электромагнитного поля, а общая напряженность электрического поля в проводящей среде равна вихревой и потенциальной составляющей
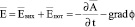 . (10)
. (10)
Из векторной алгебры известно, что ротор градиента любого скаляра равен нулю т.е. rotgradj = 0. Поэтому выражения (9) и (10) в равной степени удовлетворяют второму уравнению Максвелла (2), что не приводит к изменению значений магнитной индукции и напряженности электрического поля. Таким образом, с помощью уравнений (7) и (9) потенциалы поля могут быть определены только с точностью до градиента некоторого произвольного скаляра j. Инвариантность поля по отношению к этому классу преобразований его потенциалов называют калибровочной или градиентной инвариантностью [6]. То есть уравнение (2) может иметь бесконечное множество решений для определения E и B.
Для устранения указанной неопределенности при нахождении потенциалов их следует подчинять дополнительному условию, задаваемому специальной калибровкой или нормировкой потенциалов и однозначно определить значения E и B [6].
Плотность тока в проводящей среде согласно закону Ома в дифференциальной форме с учётом (10) можно представить в виде
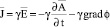 ,
,
где γ – электропроводность проводящей среды.
Калибровка потенциалов может быть получена на основании первого уравнения Максвелла (1) с учетом (6) и (7).
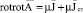 . (11)
. (11)
На основании (4) и (10) уравнение (11) запишем в следующем виде:
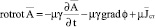 . (12)
. (12)
Согласно векторному анализу можем записать
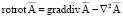 . (13)
. (13)
Поэтому уравнение (12) с учетом (13) запишем следующим образом:
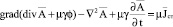 . (14)
. (14)
Так как величины 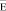 и
и 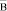 могут быть теоретически определены бесчисленным множеством взаимосвязанных значений
могут быть теоретически определены бесчисленным множеством взаимосвязанных значений  и j, т.е. значение j можно определять по произволу и все это должно удовлетворять уравнениям (8) и (12). Поэтому для того чтобы упростить уравнение (14) и связать однозначно
и j, т.е. значение j можно определять по произволу и все это должно удовлетворять уравнениям (8) и (12). Поэтому для того чтобы упростить уравнение (14) и связать однозначно 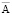 и j, калибровку потенциалов целесообразно записать в виде
и j, калибровку потенциалов целесообразно записать в виде
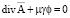 ,
,
откуда
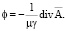 (15)
(15)
При введении калибровки (15) скалярный потенциал j из уравнения (14) исключается и устраняется неопределенность при определении 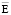 и
и 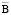 , а уравнение (14) значительно упрощается
, а уравнение (14) значительно упрощается
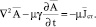 (16)
(16)
Уравнение (16) однозначно выражается только через векторный потенциал  и после его определения значение j достаточно просто найти из калибровки (15).
и после его определения значение j достаточно просто найти из калибровки (15).
В электропроводящих средах в общем случае принимать значение 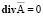 нельзя, кроме некоторых частных случаев. Это часто встречаемая ошибка при попытке получить уравнение электромагнитного поля с помощью векторного потенциала. В реальных условиях векторный потенциал электромагнитного поля имеет три составляющие, направленные по осям x, y, z в декартовой системе координат, поэтому калибровка (15) запишется в виде
нельзя, кроме некоторых частных случаев. Это часто встречаемая ошибка при попытке получить уравнение электромагнитного поля с помощью векторного потенциала. В реальных условиях векторный потенциал электромагнитного поля имеет три составляющие, направленные по осям x, y, z в декартовой системе координат, поэтому калибровка (15) запишется в виде
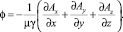 (17)
(17)
При решении двухмерных и трехмерных задач по расчету электромагнитного поля, когда векторный потенциал имеет две или три составляющих, скалярный потенциал j согласно (17) не может быть равен нулю.
В ряде частных случаев скалярный потенциал j можно положить равным нулю. При этом расчет электромагнитного поля сводится к определению векторного потенциала 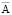 , на который должно быть наложено условие
, на который должно быть наложено условие 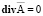 . Такое упрощение становится возможным, если векторный потенциал имеет только одну составляющую, направленную вдоль одной из координатных осей. Причем его величина от этой координаты не зависит. Правомерность такого подхода к решению задачи подтверждается исследованиями электромагнитного поля на базе одномерных моделей электрических машин с электропроводящей средой, имеющей неограниченные размеры. При ограниченных размерах электропроводящей среды свободное растекание токов становится невозможным, что обуславливает появление потенциальной составляющей электрического поля
. Такое упрощение становится возможным, если векторный потенциал имеет только одну составляющую, направленную вдоль одной из координатных осей. Причем его величина от этой координаты не зависит. Правомерность такого подхода к решению задачи подтверждается исследованиями электромагнитного поля на базе одномерных моделей электрических машин с электропроводящей средой, имеющей неограниченные размеры. При ограниченных размерах электропроводящей среды свободное растекание токов становится невозможным, что обуславливает появление потенциальной составляющей электрического поля
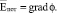
Следует отметить, что в электропроводящих средах кроме калибровки потенциалов (15) теоретически возможно применить бесчисленное множество различных калибровок, но непременным условием их применения должно быть значительное упрощение выражения (12) и выполнение условия 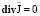 [1].
[1].
В данной статье рассматривается расчёт электромагнитного поля в изотропных неподвижных электропроводящих средах. Вопрос калибровки потенциалов поля в анизотропных средах изучен крайне недостаточно. В работе [2] рассматривается электромагнитное поле в анизотропной электропроводящей среде, неподвижной относительно системы координат. Магнитные проницаемости и электропроводности по двум координатным осям принимаются одинаковыми. В этом случае используется калибровочное уравнение вида
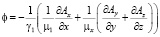 ,
,
где γ1 = γy = γz и μ1 = μy = μz.
Для других типов анизотропии и для сред движущихся относительно системы координат, калибровочные уравнения неизвестны. Указывается только то, что можно получить систему уравнений, в каждом из которых будут содержаться производные только одной из проекций вектора. При этом уравнения имеют четвёртый порядок и довольно громоздкий вид.
В общем случае для калибровки потенциалов целесообразно положить условие, заведомо справедливое во всех точках электропроводящей среды и независимое от анизотропии магнитных проницаемостей и электропроводимостей по координатным осям.
Как показали исследования, в качестве такого условия наиболее целесообразно использовать 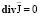 , которое с учётом уравнения
, которое с учётом уравнения 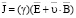 приводится к виду
приводится к виду
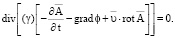
Все эти ограничительные условия значительно усложняют расчеты специальных электрических машин.
Заключение
На основе представленной методики коллективом авторов были разработаны методы расчета электромагнитных процессов в специальных электрических машинах, в частности в ЦЛВД [8], полностью удовлетворяющие требованиям по простоте, скорости расчета и точности. Разработана также микропроцессорная система управления цилиндрическим линейным вентильным двигателем возвратно-поступательного движения [4].
Результаты, представленные в статье, получены при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.310068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).
Библиографическая ссылка
Огарков Е.М., Ключников А.Т., Коротаев А.Д., Чирков Д.А. РАСЧЕТ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В НЕПОДВИЖНЫХ ЭЛЕКТРОПРОВОДЯЩИХ ИЗОТРОПНЫХ СРЕДАХ // Фундаментальные исследования. 2016. № 12-1. С. 91-95;URL: https://fundamental-research.ru/ru/article/view?id=41052 (дата обращения: 08.03.2026).



