Метод опорных элементов разработан с учетом отечественного и зарубежного опыта проектирования плана трассы. Он применен к принципам клотоидного трассирования, когда трасса, в геометрическом смысле, представляет последовательность соответствующим образом сопряженных отрезков круговых кривых, клотоид, отрезков клотоид и прямых.
Условимся называть опорными элементами трассы – круговые кривые и прямые, а связующими – клотоиды или отрезки клотоид, сопрягающие смежные опорные элементы [2].
Метод опорных элементов основан на принципе аналитической увязки смежных опорных элементов. Принципиальное отличие этого метода от ранее применяемых заключается в том, что определяющими элементами как при графической проработке, так и при аналитическом расчете трассы являются опорные элементы, то есть прямые и круговые кривые.
Предусмотрены различные типы и способы задания опорных элементов, представленные на рис. 1 [5].
При разработке метода опорных элементов рассмотрены всевозможные комбинации элементов трассы, которые могут встретиться в практике трассирования. На основе анализа этих комбинаций все расчетные случаи систематизированы в три группы, представленные на рис. 2, характеризующиеся определенным взаимным расположением опорных элементов и их видом. Для наглядного представления вида опорных элементов на расчетных схемах (см. рис. 2) условно показан один, наиболее распространенный, способ задания опорных элементов. В практике же могут быть использованы любые способы задания для соответствующего вида опорного элемента, которые представлены на рис. 1.
Математические зависимости расчета геометрии трассы по методу опорных элементов довольно сложны, отдельные блоки могут быть решены только итерационными методами. По этой причине проектирование трассы по предлагаемому методу целесообразно выполнять с использованием ЭВМ. В данной статье не представляется возможным показать весь алгоритм, поэтому продемонстрируем подход к решению задачи на примере одного расчетного случая 1–3 (см. рис. 3).
1. Вычисляют расстояние между центрами круговых кривых М1 и М4 с координатами ХМ1, YМ1 и ХМ4, YМ4:
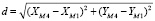 . (1)
. (1)
2. Проверяют правильность задания исходной информации. Если 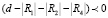 , то имеется ошибка в задании исходной информации и необходимо внести в нее изменения. Геометрически это представляется как пересечение круговых опорных элементов, задача в этом случае не имеет смысла. При
, то имеется ошибка в задании исходной информации и необходимо внести в нее изменения. Геометрически это представляется как пересечение круговых опорных элементов, задача в этом случае не имеет смысла. При 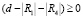 продолжают расчет.
продолжают расчет.
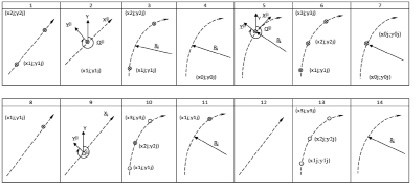
Рис. 1. Способы задания опорных элементов: 1–7 – фиксированные; 8–11 – полуфиксированные; 12–14 – свободные;  – фиксированные точки;
– фиксированные точки;  – приближенные точки
– приближенные точки
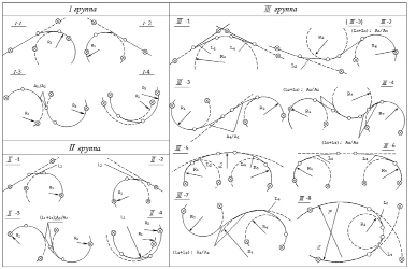
Рис. 2. Расчетные схемы метода опорных элементов
Из геометрических построений, приведенных на рис. 3:
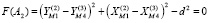 (2)
(2)
где 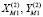 – координаты центра первой круговой кривой относительно системы
– координаты центра первой круговой кривой относительно системы 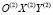 ;
;
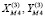 – координаты точки М4 относительно системы
– координаты точки М4 относительно системы 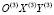 .
.
Введем следующие обозначения:
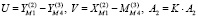 ,
,
тогда
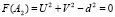 ,
,
где
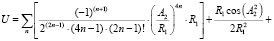
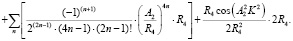
В данных и последующих формулах ряды, представленные в виде суммы, являются быстросходящимися. Количество членов ряда определяют из условия обеспечения требуемой точности расчетов [Е], то есть пока не будет выполнено условие 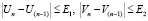 и т.д.
и т.д.
3. Уравнение F(A2) = 0 может быть решено относительно А2 только численными методами. В данном случае удобнее всего воспользоваться методом Ньютона, поскольку имеется возможность определить приближенное значение параметра А2, используя эмпирическую формулу.
Экспериментальные исследования, приведенные на компьютере с помощью специально разработанной программы, показали сходимость этого метода в области определения функций F(A2), для которой
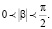
4. Для решения уравнения необходимо продифференцировать выражение F(A2) по (А2):
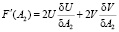 , (3)
, (3)
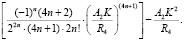
Первое приближенное значение параметра А2 можно определить по формуле
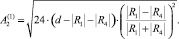 (4)
(4)
Затем вычисляют 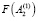 и
и 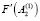 .
.
5. Приращение аргумента определим по формуле
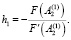 (5)
(5)
Далее находят второе приближение параметра первой ветви клотоиды 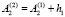 , вычисляют
, вычисляют 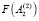 и
и 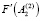 и т.д.
и т.д.
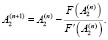 (6)
(6)
Расчет производят до тех пор, пока не будет выполнено условие
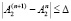 ,
,
где Δ – точность определения параметра. Затем определяют А3 по формуле
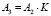 .
.
На рис. 3 показано правило знаков, геометрических характеристик в частной системе отсчета в зависимости от направления расчета трассы.
Проектирование трассы по методу опорных элементов можно осуществлять по материалам аэрофотосъёмки, топографическим планам или картам в абсолютной или условной системе координат. Данный метод может быть также использован при комплексном трассировании с применением цифровых моделей местности. Для этого в программах, реализующих метод опорных элементов, предусмотрен блок вычисления координат главных и промежуточных точек трассы с заданным интервалом между ними или точек, соответствующих определенному пикетажному положению. На топооснове по общепринятым принципам от руки или с помощью гибкой линейки с учетом всех ограничений намечают в первом приближении положение трассы автомобильной дороги. Полученную таким образом плавную кривую необходимо разложить на последовательность, состоящую из круговых кривых, клотоид и прямых, отвечающую определенным требованиям. Геометрические характеристики элементов должны находиться в определенных пределах, зависящих от конкретных условий и прежде всего от расчетной скорости, принятой для проектируемой дороги.
Регламентируются: отношения длин смежных элементов, величины и отношения радиусов смежных закруглений и зависимости параметров клотоид от величин радиусов закруглений, к которым они примыкают. Должны выдерживаться также определенные рекомендации по сочетанию элементов плана и по взаимной увязке их с элементами продольного профиля.
Рассмотрим несколько примеров применения предполагаемого метода.
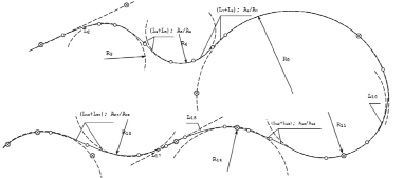
На рис. 4, а представлен участок лесной автомобильной дороги, запроектированной по методу опорных элементов с применением шаблонов круговых кривых.
На основе анализа условий, влияющих на проложение трассы, на топооснове наносят контрольные точки и от руки или с помощью гибкой линейки намечают предварительное положение трассы.
Анализируют полученную таким образом линию и устанавливают предварительную последовательность элементов без установления их величины и границ. Пользуясь шаблонами круговых кривых, определяют положение опорных элементов. В результате графической проработки трассы получают все данные, необходимые для расчета, и устанавливают ориентировочные границы элементов трассы, что дает возможность проектировщику уже на этом этапе работ отчетливо представлять всю геометрию трассы и проводить анализ выполнения предъявляемых к трассе требований.
a)

б)
Рис. 3. Пример проектирования трассы: а) с применением шаблонов; б) без применения шаблонов
а)
б)
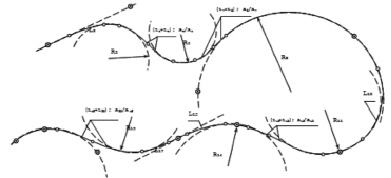
Рис. 4. Пример проектирования трассы: а) с применением шаблонов; б) без применения шаблонов
В зависимости от конкретных условий устанавливают последовательность расчетных случаев, способы задания опорных элементов и необходимые данные по связующим элементам.
Так, случай 1 группы наиболее целесообразно использовать в свободных условиях проложения трассы в плане, когда представляется возможным применять длины переходных кривых значительно большие, чем минимальные, которые рекомендуются нормами, а также для «увязки» на концах участков и вариантов [6].
Расчетные случаи II и III группы наиболее часто применяют в практике проектирования, поскольку с их использованием в лучшей степени можно контролировать геометрию трассы и строго выдерживать предварительную разбивку трассы на элементы, выполненную проектировщиком.
Расчетные случаи III группы могут быть применены как для расчета промежуточных участков трассы, так и для «увязки» в местах примыкания к существующим дорогам или ранее рассчитанным участкам трассы.
При проектировании с использованием шаблонов круговых кривых обычно используют способы задания опорных элементов [1, 3, 4, 8, 10].
Проектирование трассы по описанной выше технологии позволяет свести до минимума отклонения расчетной трассы от графически проработанной. Экспериментальным путем установлено, что эти отклонения, как правило, не превышают 1 мм в масштабе плана. Это является вполне удовлетворительным при проектировании автомобильных дорог в самых сложных условиях, где предъявляются жесткие требования к проложению трассы (в горной местности, при реконструкции дорог и т.д.).
На рис. 4, б показан пример проектирования трассы без применения шаблонов. Расчет трассы в этом случае целесообразно осуществлять по схемам II и III групп. Проработку трассы производят следующим образом. Сначала из всей последовательности элементов трассы (рис. 4, б), намеченной с помощью гибкой линейки, выделяют прямолинейные участки и задают их по способу 1, 8 или 12. Затем визуально отмечают точки с минимальным радиусом кривизны (22, 23, …, 2j) и точки перегиба трассы (02, 03, …, 0j). Положение крайних точек для каждого кругового элемента может быть намечено из условия, что 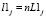 и
и 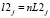 , причем на основании анализа проектной практики можно рекомендовать назначать величину коэффициента n дифференцировано от n = 0,2 в стесненных условиях проложения трассы до n = 0,5 в свободных условиях. Длины связующих элементов, а для S-образных закруглений суммарные длины двух смежных ветвей клотоид и соотношение их параметров могут определяться программно или задаваться проектировщиком [7, 9].
, причем на основании анализа проектной практики можно рекомендовать назначать величину коэффициента n дифференцировано от n = 0,2 в стесненных условиях проложения трассы до n = 0,5 в свободных условиях. Длины связующих элементов, а для S-образных закруглений суммарные длины двух смежных ветвей клотоид и соотношение их параметров могут определяться программно или задаваться проектировщиком [7, 9].
При проектировании лесных автомобильных дорог часто возникает необходимость перехода на самостоятельное трассирование по направлениям движения. Как известно, переход на разделительное трассирование по направлениям движения рекомендуется осуществлять на криволинейных участках в целях обеспечения плавного вида дороги, исключающего возможность неправильного ориентирования водителя относительно дальнейшего направления движения.
Подобным образом могут быть решены и другие проектные задачи, например увязка вариантов трассы на криволинейных участках, примыкания к криволинейным осям проектируемых и существующих сооружений и др. С применением метода опорных элементов может быть также рассчитана геометрия закруглений автомобильных дорог с автономным расчетом кромок и бровок по закономерностям клотоидной трассы. Как известно, на кривых малых радиусов устраивают уширения проезжей части. Обычно, эти уширения выполняют на протяжении переходной кривой пропорционально расстоянию от начала переходной кривой так, чтобы величины полного уширения были достигнуты к началу круговой кривой.
Выводы
В результате проведенного исследования можно сделать следующие выводы:
– метод опорных элементов, по сравнению с традиционным, позволяет существенно облегчить и упростить процесс графической проработки трассы, поскольку исключается необходимость использования шаблонов клотоидных кривых для подбора параметров;
– предусмотрено автоматическое выполнение ряда требований трассирования, расширились его возможности за счет увеличения набора расчетных схем.
Библиографическая ссылка
Козлов В.Г., Скрыпников А.В., Ломакин Д.В., Логойда В.С. МЕТОДОЛОГИЧЕСКОЕ ОБОСНОВАНИЕ ОСОБЕННОСТЕЙ ПРОЕКТИРОВАНИЯ ТРАССЫ ПО МЕТОДУ ОПОРНЫХ ЭЛЕМЕНТОВ // Фундаментальные исследования. 2016. № 12-1. С. 62-68;URL: https://fundamental-research.ru/ru/article/view?id=41047 (дата обращения: 08.03.2026).



