В современных конструкциях механических передач гиперболоидные передачи не нашли широкого применения. Это обусловлено в первую очередь тем, что изготовление гиперболоидных зубчатых колес представляет собой трудную технологическую задачу. Однако ряд конструктивных преимуществ позволяет найти им сферу применения, несмотря на существенно большие затраты на изготовление по сравнению с другими типами передач. В частности, в отличие от гипоидных передач, гиперболоидные позволяют передавать одинаковую мощность как в прямом, так и в реверсном направлении. В отличие от червячных передач, гиперболоидные могут иметь передаточные отношения в диапазоне от 0,2 до 5...10 (ограничения накладываются при оценке величин потерь на трение и по удельным нагрузкам в диапазоне приемлемых скоростей скольжения). Коэффициент полезного действия гиперболоидных передач оценивается в диапазоне до 0,96...0,98.
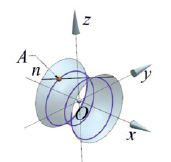
При моделировании боковой поверхности зубьев сопряженных гиперболоидных колес возможно использование подхода, позволяющего рассчитать гиперболоидные винтовые линии, заданные в сечениях делительного гиперболоида, гиперболоидов в основании и на вершине зуба. При моделировании с использованием сечения и трех направляющих. Для сопряженных колес согласованными винтовыми линиями будут линии, лежащие на делительных гиперболоидах. Уравнения этой линии, для обоих колес, работающих в паре, можно рассчитать кинематически, а также непосредственно смоделировать. В предположении, что делительные гиперболоиды колес образуются вращением линии n (рис. 1) вокруг каждой из перекрещивающихся осей колес передачи (на рисунке изображен один из гиперболоидов).
 а)
а) 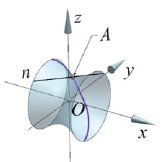 б)
б)
Рис. 1. Гиперболоидная винтовая линия при различных значениях скорости движения точки А вдоль линии n. Для а) скорость движения вдоль линии n, чем для б)
В предположении, что точка А движется по линии n со скоростью v(t), перекрещивающейся с осью x под углом β, а сама линия, образующая гиперболоид, вращается вокруг оси x с угловой скоростью ω(t), уравнение винтовой линии примет вид [7]:
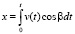 ;
;
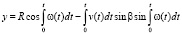 ; (1)
; (1)
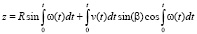 ,
,
где R – радиус гиперболоида в горловом сечении; β – угол перекрещивания оси x и линии n.
Для передачи, из условия равномерного вращения обоих колес пары, представляет интерес случай v = const и ω = const. Варьируя v при заданном значении ω, можно получать различные значения шага и, соответственно, угла подъема винтовой линии. Так как одна и та же точка A используется для расчета винтовых линий колес, работающих в паре, то эти винтовые линии будут использоваться для моделирования сопрягаемых боковых поверхностей зубьев. Моделирование боковых может осуществляться по сетке кривых: направляющими линиями будут винтовые линии, линиями сечений отрезки производящей линии [4]. Моделирование может осуществляться по сечениям в плоскостях, перпендикулярных оси вращения колеса [1, 3].
Для ортогональной передачи, при условии использования в качестве образующей отрезка прямой, заданной в нормальном сечении к боковой поверхности зуба, проведенном из горлового сечения, можно рассчитать частный вариант сопряженных боковых поверхностей зубчатых колес, работающих в паре, без расчета винтовой линии. В данном случае боковая поверхность зуба моделируется посечением и представляет собой линейчатую поверхность. Характер кривизны боковой поверхности зуба в горловом сечении меняется от вогнутой на выпуклую. Следовательно, расчет должен осуществляться для каждой половины боковой поверхности зуба по отдельному алгоритму, суть которых приводится ниже.
Осью вращения первого колеса является ось вращения O1X1 (рис. 2). Осью вращения второго колеса является ось O2Y2. Для расчета половин зубьев первого и второго колес положим, что отрезок образующей АВ вращается равномерно вокруг оси O2Y2 с постоянной угловой скоростью ω2 – относительное движение в системе координат O2X2Y2Z2. Данное движение можно задать для двух точек А и В, принадлежащих образующей:
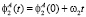 ;
;
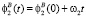 , (2)
, (2)
где 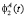 ,
, 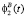 – углы поворота точек A и B при равномерном вращении образующей вокруг оси Y2 в системе координат O2X2Y2Z2, t-параметр (условно время) способный принимать как положительные, так и отрицательные значения.
– углы поворота точек A и B при равномерном вращении образующей вокруг оси Y2 в системе координат O2X2Y2Z2, t-параметр (условно время) способный принимать как положительные, так и отрицательные значения.
Система координат O1X1Y1Z1 принята за неподвижную, и гиперболоидное колесо, осью вращения которой является ось O1X1 примем за неподвижное и положим, что колесо, осью вращения которого является O2Y2 вместе с системой координат O2X2Y2Z2 равномерно вращается вокруг оси O1X1 с угловой скоростью ω1 = ω2/i, где i – передаточное отношение, равное отношению диаметров гиперболоидов 1 к 2 в горловых сечениях. Это будет переносным движением.
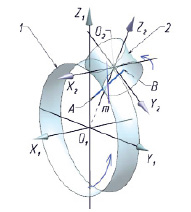
Рис. 2. К расчету боковой поверхности зуба гиперболоидного колеса. AB – «Образующая»; m – одна из двух линий пересечения делительных гиперболоидов; 1, 2 – делительные гиперболоиды колес, работающих в сопряжении
Траектории абсолютного движения рассчитываются отдельно для точки A и точки B, как векторные суммы относительных и переносных движений:
O1A = O1O2 + O2A;
O1B = O1O2 + O2B, (3)
где O1A, O1B – радиус-векторы положений точек А и В в системе координат O1X1Y1Z1, O1O2 – радиус-вектор положения точки O2 в системе координат O1X1Y1Z1, O2A, O2B – радиус-векторы положений точек A и B в системе координат O2X2Y2Z2. Расчет проводится для четырех половин двух поверхностей, работающих в сопряжении. Рассмотрим методику расчета для одной второй боковой поверхности зуба колеса 1.
Колесо 1 предполагается неподвижным, система координат O1X1Y1Z1 жестко с ним связана. Колесо 2 равномерно вращается вокруг оси O1X1 угловой скоростью ω1 таким образом, что ось O2Z2 совпадает с вектором O1O2. Ось O2X2 параллельна оси O1X1. Отрезок АВ равномерно вращается вокруг оси O2Y2 с угловой скоростью ω2 = ω1/i, где i – передаточное отношение, равное отношению делительных диаметров в горловом сечении второго колеса к первому. Начальное положение точек A и B задается в плоскости, перпендикулярной линии пересечения делительных гиперболоидов и проходящей через горловые сечения, координаты точек зависят от выбранного угла зацепления. Данному положению точек A, B образующей будет соответствовать нулевое значение параметра t. С учетом того, что положение образующей, равномерно вращающейся вокруг оси O2Y2, координаты точек A и B в системе координат O2X2Y2Z2 будут определяться:
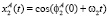 ,
,
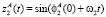 ,
,
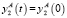 ;
;
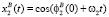 ,
,
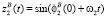 ,
,
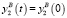 .
.
Орт-векторы системы координат O2X2Y2Z2, необходимо определить через орт- векторы системы координат O1X1Y1Z1 в зависимости от значения параметра t:
i2 = i1,
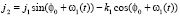 ,
,
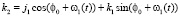 .
.
При подстановке данных выражений в уравнения (3) можем рассчитать положение образующий, зависящей от значения параметра t. При изменении t от нуля в положительном направлении получим положение сечения для половины боковой поверхности первого зубчатого колеса. Если изменять t от нуля в отрицательном направлении, получим половину боковой поверхности второго зубчатого колеса.
Затем необходимо принять колесо 2 с системой координат O2X2Y2Z2 за неподвижное, а первое вместе с системой координат O1X1Y1Z1, вращающимся вокруг оси O2Y2 c постоянной угловой скоростью ω2, таким образом, что ось O1Z1 будет совпадать по направлению с отрезком O1O2. Отрезок AB принять равномерно вращающимся с угловой скоростью ω1 вокруг оси O1X1. В этом случае также рассчитать траектории движения точек A и B как векторные суммы относительных и переносных движений. В этом случае получим вторые половины боковых поверхностей зубьев для обоих зубчатых колес.
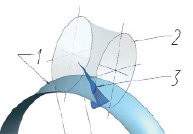
Рис. 3. Моделирование боковой поверхности зуба гиперболоидного колеса по «кривым» сечений: 1 – делительный гиперболоид колеса, для которого моделируется боковая поверхность зуба; 2 – делительный гиперболоид сопряженного колеса; 3 – боковая поверхность зуба колеса 1
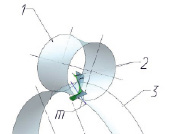
Рис. 4. Совмещенные поверхности зубьев, участвующих в зацеплении. 1 – делительный гиперболоид ведущего колеса; 2 – сопряженные боковые поверхности зубьев; 3 – делительный гиперболоид ведомого колеса
Полученные совокупности координат точек образующих позволяют смоделировать боковую поверхность зуба гиперболоидного зубчатого колеса (рис. 3). Одновременно в результате расчета получаем также координаты образующей, для моделирования боковой поверхности зуба сопряженного колеса (рис. 4). При этом с учетом необходимых коррекций образующей линии [6] могут быть получены уравнения координат точек модифицированных образующих линий.
Данную кинематику формообразования можно непосредственно реализовать в компьютерной среде моделирования механизмов, например в среде «Симуляция кинематических механизмов» системы NX.
Рис. 5. Гиперболоидные зубчатые колеса, работающие в паре
В результате расчета боковых поверхностей зубьев получаем поверхности, гарантированно перекрывающие область между поверхностями вращения, образованными ножкой и вершиной зубьев. По аналогии с эвольвентными зубчатыми колесами используем соотношения: головка зуба равна модулю m, ножка зуба равна 1,25m в любом сечении, перпендикулярном оси вращения рассматриваемого колеса. При этом, так как зубчатый венец моделируется на гиперболоиде вращения, то в горловом сечении модуль будет минимальным. Наличие двух поверхностей зуба, либо впадины, позволяет смоделировать зубчатый венец. Остальные элементы геометрии зубчатых колес гиперболоидной передачи моделируются с учетом требований конструкции, как, например, рис. 5.
Наличие геометрических моделей позволяет изготовлять опытные образцы гиперболоидных зубчатых колес на пятикоординатных станках с ЧПУ [5], либо выращивать данные детали методами аддитивных технологий. Были предложены также методы изготовления гиперболоидных зубчатых колес на зубообрабатывающих станках [2].
Библиографическая ссылка
Абзалов А.Р., Иванова В.Н., Яруллина Д.Е. РАСЧЕТ БОКОВЫХ ПОВЕРХНОСТЕЙ ЗУБЬЕВ И МОДЕЛИРОВАНИЕ ЗУБЧАТЫХ КОЛЕС ОРТОГОНАЛЬНЫХ ГИПЕРБОЛОИДНЫХ ПЕРЕДАЧ // Фундаментальные исследования. 2016. № 12-1. С. 9-13;URL: https://fundamental-research.ru/ru/article/view?id=41038 (дата обращения: 27.01.2026).



