Математические методы широко используются для исследования зависимостей в медицине, экономике и других областях деятельности человека. Универсальный математический аппарат позволяет применять корреляционный и регрессионный анализ в любой предметной области, таким образом, возможно его использование в электроэнергетике, например, для определения зависимостей с целью эффективного управления процессами. В работах [3, 7] рассматриваются подходы к минимизации потерь активной мощности, зависящей от показателей качества электроэнергии (ПКЭ), однако они рассматривают лишь методы управления отдельными показателями, но не улучшение показателей качества в комплексе. В работах [4–6] приводились комплексные аспекты управления в электроэнергетике, в том числе рассматривалась актуальность создания системы управления ПКЭ, приведены три основных этапа её построения и проводился корреляционный анализ нескольких пар показателей на основе малой выборки, она позволила провести лишь поверхностное исследование.
В качестве объекта исследования были использованы выборки показаний регистратора ПКЭ, полученные при измерениях в системе электроснабжения одного из месторождений нефти и газа ООО «ЛУКОЙЛ-ПЕРМЬ», – коэффициент третьей гармонической составляющей и коэффициент искажения синусоидальности напряжения. Показания снимались в течении 7 дней, за это время в системе происходили различные переключения, что приводило к изменению значений коэффициентов. На рис. 1 выборочно представлены результаты измерений за 2 часа коэффициента третьей гармоники и коэффициента искажения синусоидальности.
Первым этапом исследования взаимозависимости между величинами является определение их закона распределения. Анализ выборки показал, что распределение значений не соответствует законам нормального распределения и следует использовать методы непараметрического корреляционного анализа, основанные на применении порядковых статистик. Такие методы, обладая повышенной устойчивостью к отклонениям распределения от нормального, в большинстве случаев позволяют упростить вычисления, оставляя на приемлемом уровне статистические характеристики получаемых заключений по гипотезам.
Гипотеза о наличии корреляции проверялась при помощи критерия Кенуя, описанного в [2]. Наличие зависимости также возможно проверить с помощью методов ранговой корреляции, но в данном случае нас не интересует количественная характеристика связи, поэтому достаточно так называемого «быстрого» критерия Кенуя. Согласно этим методикам было проверено наличие корреляции для пары: коэффициент третьей гармонической составляющей KU(3) фазы А и коэффициент искажения синусоидальности кривой напряжения KUA.
Критерий Кенуя был применен для нескольких выборок длиной от 81 до 10047 строк. Выборка длиной в 81 строку – наименьшая выборка, при которой расчеты по критерию Кенуя еще определяли, что между рассмотренной парой коэффициентов связь присутствует с доверительной вероятностью 0,99.
Далее необходимо вывести закон, которому подчиняется выбранная пара коэффициентов. В первую очередь была проведена проверка на соответствие линейному закону. Линейный регрессионный анализ исходит из наличия зависимости y = a + bx, где a и b – неизвестные коэффициенты регрессии, а x и y – значения переменных. Оценка коэффициентов регрессии выполняется методом наименьших квадратов, описанным в [1, 2].
В результате получается функция максимально приближенная к истинному закону. Для оценки качества построенной модели используется средняя ошибка аппроксимации, вычисленная по формуле
,
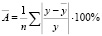где n – количество пар расчетных и фактических значений, y – фактическое значение функции,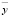 
– расчетное значение функции. Допустимый предел значений средней ошибки аппроксимации не более 8–10 %. Подобным образом возможно провести оценку влияния на коэффициент искажения синусоидальности остальных коэффициентов гармонических составляющих.
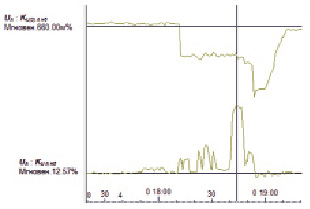
Рис. 1. Графики изменения коэффициента третьей гармоники и коэффициента искажения синусоидальности за двухчасовой период
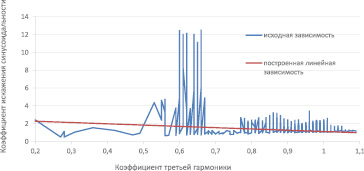
Рис. 2. График зависимости при выборке размером 10047 строк
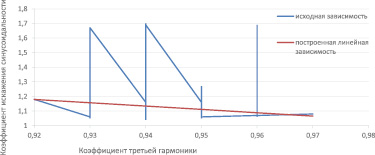
Рис. 3. График зависимости при выборке размером 81 строка
Таблица 1
Результаты проверки на соответствие линейному закону
|
Количество строк (время измерения) |
Число n, отвечающее за наличие связи |
Функция |
Среднее отклонение, % |
|
10047 (7 дней) |
2245 |
y = 2,56 – 1,44 х |
12,46 |
|
5030 (3,5 дня) |
1249 |
y = 3,73 – 2,6 х |
13,52 |
|
2520 (1,75 дня) |
930 |
y = 4,62 – 3,5 х |
16,2 |
|
1455 (1 день) |
441 |
y = 5,01 – 3,92 х |
17,73 |
|
735 (12 часов) |
239 |
y = 0,16 – 1,05 х |
9,67 |
|
195 (3 часа) |
161 |
y = 3,1 – 2,07 х |
5,21 |
|
81 (примерно 1,5 часа) |
112 |
y = 3,28 – 2,28 х |
6,19 |
Результаты проверок на наличие корреляции и соответствие линейному закону представлены в табл. 1.
Выборки, состоящие из разного количества строк, дают разную среднюю ошибку аппроксимации. Начиная с количества 1455 строк и более, среднее отклонение от линейного закона уменьшается и в итоге равняется 12,46 % при 10047 строках. А при меньшем количестве строк среднее отклонение уже не имеет прямо пропорциональной зависимости от количества строк. Предполагается, что существует оптимальное количество строк, при котором линейная функция будет наиболее точно описывать взаимодействие этих двух коэффициентов.
Графики зависимости коэффициента искажения синусоидальности от коэффициента третьей гармоники для выборок в 10047 и 81 строк представлены на рис. 2 и 3.
Если ошибка аппроксимации слишком большая, даже при достаточных размерах выборки, то влияние коэффициента гармонической составляющей следует описывать каким-нибудь более сложным законом. Для любой системы независимо от происходящих в ней переключений и вида нагрузок алгоритм в общем виде будет выглядеть одинаково. Сами функции необходимо корректировать в каждом отдельном случае, в зависимости от вида подключаемой нагрузки. Исходя из вышесказанного алгоритм для оценки влияния гармонических составляющих на коэффициент искажения синусоидальности сформулирован следующим образом:
1. Первый этап – определение закона распределения значений коэффициентов. В случае, если значения подчиняются закону нормального распределения, то следует определять зависимость классическим коэффициентом Пирсона, в противном случае переходим к второму этапу.
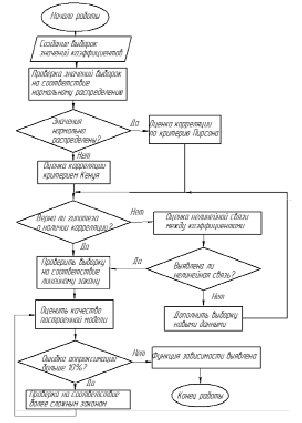
Рис. 4. Алгоритм оценки влияния гармонических составляющих на коэффициент искажения синусоидальности
2. Второй этап – корреляционный анализ. Создается первоначальная выборка значений коэффициентов попарно соотнесенных между собой. Затем производится оценка корреляции с помощью критерия Кенуя. Если гипотеза о наличии корреляции верна, то происходит переход к следующему этапу – регрессионному анализу. Но выборка может иметь слишком малое количество значений для того, чтобы достоверно проверить наличие корреляционной связи, поэтому в случае отсутствия связи выборку следует проверить на наличие нелинейной корреляционной связи, либо пополнять её новыми значениями.
3. Третий этап – регрессионный анализ. Выборку необходимо оценить на соответствие линейному закону, дать оценку коэффициентов регрессии, например, обобщенным методом наименьших квадратов. Затем полученная функция должна пройти проверку адекватности, для этого следует найти среднюю ошибку аппроксимации. И если ошибка аппроксимации менее 10 %, то считается, что проверка на адекватность пройдена успешно и данный линейный закон достаточно точно описывает взаимосвязь выбранной пары коэффициентов. В противном случае необходимо перейти к проверке на соответствие более сложным законам.
Данный алгоритм кратко представлен в виде блок-схемы на рис. 4.
Проверку на соответствие более сложным законам проводят с использованием линеаризующих функциональных преобразований, а затем выявленный закон аналогично проверяется на адекватность нахождением средней ошибки аппроксимации [4]. Представленный алгоритм является довольно простым, содержит в себе два цикла. В последующем предполагается проведение дополнительных исследований для нахождения оптимальной выборки данных необходимой для достоверного определения наличия корреляционной связи между парами коэффициентов.
Библиографическая ссылка
Павлов Н.В., Лейзгольд К.А., Ромодин А.В. ОЦЕНКА ВЛИЯНИЯ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ НА КОЭФФИЦИЕНТ ИСКАЖЕНИЯ СИНУСОИДАЛЬНОСТИ В СИСТЕМЕ ЭЛЕКТРОСНАБЖЕНИЯ ПРОМЫШЛЕННОГО ПРЕДПРИЯТИЯ // Фундаментальные исследования. – 2016. – № 11-3. – С. 578-582;URL: https://fundamental-research.ru/ru/article/view?id=41020 (дата обращения: 23.11.2024).