Одними из первых исследователей, применивших в кинобизнесе метод экономико-математического моделирования, были Прэг и Касавант, которые в 1994 г. опубликовали статью [5] с сообщением о создании регрессионной модели на основе выборки из 625 американских фильмов. Рассматриваемый ими набор входных переменных включал производственный бюджет, критические обзоры, наличие звезд, наличие франшизы, наличие премий, жанр и рейтинг.
Аппарат нейронных сетей для прогнозирования кассовых сборов фильмов был впервые применен в 2002 г. американскими учеными R. Sharda и D. Delen. В 2006 г. эти же авторы [6] построили модели на основе логистической регрессии, дискриминантного анализа, классификационного и регрессионного дерева, а также нейронной сети, показавшей наилучший результат.
Целью настоящей работы является создание нейросетевой экономико-математической модели и ее реализация в виде программной системы, позволяющей прогнозировать кассовые сборы кинофильмов, рассчитывать и оптимизировать прибыль в зависимости от параметров кинофильма, а также проводить исследование закономерностей кинобизнеса. Актуальность создания такого инструмента обусловлена высоким уровнем конкуренции в данном сегменте рынка, необходимостью строгого расчета бюджета фильма, выбора сценария, подбора актеров, прочих атрибутов фильма, понимания закономерностей кинобизнеса и принятия на этой основе научно обоснованных решений.
При построении нейросетевой экономико-математической модели в качестве входных параметров были выбраны следующие:
X1 – Бюджет фильма, выраженный в долларах США.
X2 – Год выпуска фильма.
X3 – Произведение, ставшее основой сценария: 1 – Компьютерная игра, 2 – Комиксы, 3 – Книга, 4 – Никакое, 5 – Пьеса.
X4 – Возрастное ограничение: 1 – от 0 лет, 2 – от 6 лет, 3 – от 12 лет, 4 – от 16 лет, 5 – от 18 лет.
X5 – Наличие главного героя, заметно превосходящего в силе остальных: 1 – да, 0 – нет.
X6 – Наличие номинаций у актеров: 1 – да, 2 – нет.
X7 – Доминирующий жанр в фильме: 1 – Ужасы; 3 – Комедия; 4 – Мелодрама; 5 – Драма; 6 – Приключения; 7 – Боевик; 8 – Фэнтези; 9 – Фантастика.
X8 – Номинации за лучший фильм (в своём жанре): 1 – да; 0 – нет.
X9 – Наличие у режиссера номинаций: 1 – да; 0 – нет.
X10 – Наличие спецэффектов: 1 – да; 0 – нет.
X11 – Часть известной франшизы: 1 – да; 0 – нет.
Выходным параметром модели Y является величина выручки – кассовых сборов фильма, выраженная в долларах США.
Всего были собраны данные о 125 фильмах с официальных источников информации. Все множество примеров было разбито на обучающее и тестирующее в соотношении 80:20. Проектирование, оптимизация, обучение, тестирование нейронной сети и эксперименты над нейросетевой математической моделью выполнялись с помощью нейропакета [1] по традиционной методике Пермского отделения Научного совета РАН по методологии искусственного интеллекта [2, 3]. Оптимальная структура нейронной сети представляла собой персептрон, имеющий 11 входных нейронов, 1 скрытый слой, в котором 2 нейрона, а также 1 выходной нейрон. В качестве активационных функций нейронов скрытого слоя и выходного слоя использовался тангенс гиперболический, а в качестве алгоритма обучения – алгоритм упругого распространения.
Результаты тестирования нейронной сети
После оптимизации и обучения нейронной сети ее прогностические свойства проверялись на примерах тестирующего множества, которые в процессе обучения не участвовали. Средняя квадратичная относительная ошибка тестирования нейронной сети, вычисленная по формуле
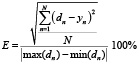 , (*)
, (*)
в которой N – количество элементов выборки, dn – фактический кассовый сбор n-го фильма, yn – его прогнозная величина, составила 11 %. Коэффициент детерминации R2 = 0,88.
Анализ влияния параметров фильма на величину кассовых сборов
После того, как на тестовых примерах оценена погрешность нейросетевой математической модели и, таким образом, доказана ее адекватность моделируемой предметной области, можно утверждать, что в пределах своей погрешности нейросетевая модель реагирует на изменения входных параметров так же, как вела бы себя сама моделируемая предметная область [4]. Следовательно, производя виртуальные изменения входных параметров модели (параметров фильмов) и наблюдая за результатами нейросетевых вычислений, можно изучать закономерности моделируемой предметной области – кинобизнеса. Для виртуальных экспериментов были выбраны четыре фильма.
1. «Пролетая над гнездом кукушки». Бюджет фильма $3000000; год выпуска 1975; произведение, ставшее основой для сценария – книга; возрастное ограничение – от 16 лет; отсутствие главного героя, заметно превосходящего в силе остальных; у актеров есть номинации за этот фильм; доминирующий жанр в фильме – драма; есть номинации за лучший фильм; у режиссера есть в наличии номинации за предыдущие работы; спецэффекты отсутствуют; фильм не является частью известной франшизы.
2. «Волк с Уолл-Стрит». Бюджет фильма $100000000; год выпуска 2013; произведение, ставшее основой для сценария – книга; возрастное ограничение – от 18 лет; отсутствие главного героя, заметно превосходящего в силе остальных; у актеров есть номинации за этот фильм; доминирующий жанр в фильме – комедия; есть номинации за лучший фильм; у режиссера отсутствуют номинации за предыдущие работы; спецэффекты отсутствуют; фильм не является частью известной франшизы.
3. «Люди в черном». Бюджет фильма $90000000; год выпуска 1997; произведение, ставшее основой для сценария – комиксы; возрастное ограничение – от 12 лет; присутствует главный герой, заметно превосходящий в силе остальных; у актеров нет номинаций за этот фильм; доминирующий жанр в фильме – фантастика; есть номинации за лучший фильм; у режиссера имеются номинации за предыдущие работы; спецэффекты присутствуют; фильм является частью известной франшизы.
4. «Центральный вокзал». Бюджет фильма $2900000; год выпуска 1998; произведение, ставшее основой для сценария – ничего; возрастное ограничение – от 12 лет; отсутствие главного героя, заметно превосходящего в силе остальных; у актеров нет номинаций за этот фильм; доминирующий жанр в фильме – драма; есть номинации за лучший фильм; у режиссера отсутствуют номинации за предыдущие работы; спецэффекты отсутствуют; фильм не является частью известной франшизы.
Компьютерные эксперименты с нейросетевой математической моделью выполнялись методом «замораживания» [6] – путем вычислений с помощью нейронной сети при постепенном изменении какого-либо одного из входных параметров и сохранении остальных входных параметров неизменными. На рис. 1–4 приведены результаты компьютерных экспериментов с целью изучения зависимости величины кассовых сборов и условной прибыли от проката исследуемых фильмов. Под условной прибылью здесь понимается разность между кассовыми сборами фильма (выручкой) и бюджетом фильма.

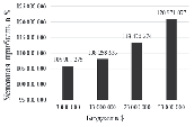
Рис. 1. Прогноз кассовых сборов и условной прибыли от проката фильма «Пролетая над гнездом кукушки» в зависимости от его бюджета


Рис. 2. Прогноз кассовых сборов и условной прибыли от проката фильма «Волк с Уолл-Стрит» в зависимости от его бюджета


Рис. 3. Прогноз кассовых сборов и условной прибыли от проката фильма «Люди в черном» в зависимости от его бюджета
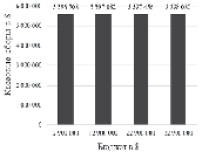
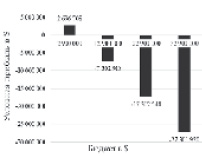
Рис. 4. Прогноз кассовых сборов и условной прибыли от проката фильма «Центральный вокзал» в зависимости от его бюджета
Как видно из рис. 1, в случае виртуального увеличения бюджета фильма «Пролетая над гнездом кукушки» на каждые 10 млн долларов, его прогнозные кассовые сборы увеличиваются приблизительно от 12 млн до 18 млн долларов США, а условная прибыль возрастает от ~ 2 млн до ~ 8 млн долларов США. Следовательно, увеличение бюджета этого фильма было бы целесообразно.
В случае увеличения бюджета фильма «Волк с Уолл-Стрит» (рис. 2) на 10 млн долларов его прогнозная условная прибыль возрастает на ~ 13 млн долларов; затем, при следующем увеличении бюджета на 10 млн долларов условная прибыль возрастает еще на ~ 8 млн долларов, затем – на ~ 4 млн долларов, а после перестает возрастать, достигая насыщения. Следовательно, бюджет этого фильма целесообразно было бы увеличить, однако не более чем на 20–30 млн долларов США.
При увеличении бюджета фильма «Люди в черном» (рис. 3), его кассовые сборы практически не изменяются, тогда как условная прибыль падает с ~ 499 млн долларов до ~ 475 млн долларов.
Увеличение бюджета фильма «Центральный вокзал» (рис. 4) нецелесообразно, поскольку его условная прибыль становится отрицательной, что означает, что фильм превращается в убыточный.
Заключение
Создана нейросетевая экономико-математическая модель, позволяющая выполнять прогнозирование кассовых сборов и условной прибыли от проката фильмов. Показано, что увеличение бюджета фильма может приводить как к увеличению прибыли кинобизнеса, так и к ее уменьшению. Модель может быть использована для оптимизации затрат на создание фильмов с целью получения наибольшей прибыли.
Библиографическая ссылка
Ясницкий Л.Н., Плотников Д.И. ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ НЕЙРОСЕТЕВАЯ МОДЕЛЬ ДЛЯ ОПТИМИЗАЦИИ ФИНАНСОВЫХ ЗАТРАТ В КИНОБИЗНЕСЕ // Фундаментальные исследования. 2016. № 11-2. С. 339-342;URL: https://fundamental-research.ru/ru/article/view?id=40977 (дата обращения: 09.01.2026).



