Сушкой называется термический процесс удаления из твердых материалов или дисперсных систем содержащейся в них влаги путем ее испарения. В процессе удаления влаги из материала конечный продукт приобретает новые свойства, которые предохраняют его от гниения и плесени, увеличивают его долговечность, предотвращают сжатие, искривление и растрескивание, также у него уменьшается масса, что ведет к удешевлению транспортировки. Меняются физические свойства материала, например снижается теплопроводность [6]. Коэффициент теплопроводности влажных материалов, согласно экспериментальным данным многочисленных исследований, значительно выше, чем коэффициент теплопроводности сухих тел. Его увеличение, согласно гипотезе А.В. Лыкова, объясняется тем, что испарение влаги происходит не только внутри или на поверхности сушимого тела, но и в небольшом пространстве над поверхностью объекта, куда выносятся микроскопические капли влаги, увлекаемые потоком сушильного агента с поверхности тела. Существующие на данный момент полуэмпирические и эмпирические зависимости позволяют рассчитывать эти коэффициенты теплопроводности. Однако определение общей продолжительности сушки до требуемого конечного влагосодержания материала, возможно лишь при известных закономерностях кинетики процесса.
Цель работы: определение фазовых характеристик влажных дисперсных систем.
Материалы и методы исследования
Объектом исследования является поведение влажных материалов во время процесса сушки при различных условиях, а также возможность его прогнозирования во времени с помощью критериев трещинообразования и коэффициентов чувствительности к сушке. На основе баланса масс между фазами, составляющими систему, производится расчет этих коэффициентов, при этом используется весовое влагосодержание.
При сушке свободнодисперсных систем использовались: сахар, крахмал и влажный шрот ягоды. Баланса массы каждого из компонентов будет достаточно для прогнозирования процесса сушки. При сушке связнодисперсных материалов, у которых известны форма и размеры используется не только баланс масс, но и баланс объемов [8]. Сумму объемных концентраций каждой из фаз для наглядности можно представить в виде выражения [2]:
Кг + Кт + Кж = 1, (1)
где Кг, Кт, Кж – соответственно содержание газовой, твердой и жидкой фазы.
Формула (1) справедлива в процессе всего времени сушки. При полном удалении влаги из высушиваемого материала уравнение (1) примет вид [2]:
Кг + Кт = 1. (2)
Использование фазовых характеристик позволяет оценить качество высушенных продуктов, а также эффективность процесса сушки. Объемные концентрации твердой фазы позволяют определить эффективность процесса сушки не только в статике, но и в динамике. Для расчетов и исследований процесса сушки используются материальный и тепловой балансы и i-d диаграмма Л.К. Рамзина [1, 3]. По данной методике можно определить необходимую температуру сушильного агента, а также рассчитать влагосодержание материала в процессе высушивания. При сушке материалов заданной формы необходимо помнить, что нужно следить не только за параметрами сушильного агента, но и за геометрическими характеристиками высушиваемого изделия, что зачастую сложно осуществить, если при этом использовать параметры влагосодержания материала. Поэтому обобщая вышесказанное, можно сделать вывод, что использование объемных характеристик позволит сократить погрешность измерений.
Показатель количества жидкого компонента в системе позволяет определить размер образовавшейся кристаллизационной структуры, а свойства твердой фазы при этом не оказывают влияния на зависимость Кт и влагосодержание материала при W ≥ Wнкв (W – влажность материала; Wнкв – наименьшая капиллярная влажность) [2]:
Kт = b•W + a, (3)
где a, b – коэффициенты, полученные эмпирическим путем.
Для того чтобы определить изменение свойств материала во время сушки, необходимо рассмотреть различие между приготовлением формовочной массы и сушкой. При этом необходимо рассматривать этот процесс, используя упрощенное представление о составе и структуре двухкомпонентных систем – структурного каркаса и парового вещества. Основная часть влаги может быть связана только поровым веществом, которое представляет из себя мелкодисперсные частицы, образующие с жидкостью суспензию. Грубодисперсные частицы суспензии образуют каркас формовочной массы и не могут удерживать большого количества влаги [4, 5].
Согласно классической технологии производства быстрорастворимых напитков после процесса грануляции, гранулы подвергаются сушке, во время которой происходит нагрев поровой суспензии [7, 9]. Для определения влияния температуры на реологические свойства паровой суспензии были проведены серии опытов. В качестве объекта исследования была принята суспензия 40 % сока аронии, шрота ягоды и крахмала. Исследуемые модельные объекты нагревались до температуры от 20 до 50 °С с шагом в 10 °С, после этого производилось термостатирование. Вследствие высокого коагуляционного структурирования исследуемых проб, время и условия подготовки опытных проб суспензии строго регламентировались и были постоянными. Результаты приведены в табл. 1 (ψ – скорость сдвига; Q – предел упругости; η – внутреннее трение)..
Таблица 1
Влияние температуры на реологические свойства суспензии
|
Реологические параметры |
Температура, °С |
|||
|
20 |
30 |
40 |
50 |
|
|
Q, дин/см2 |
270 |
290 |
340 |
470 |
|
η1, пуаз |
2,24 |
1,68 |
1,26 |
1,02 |
|
ψ1, сек-1 |
113 |
121 |
142 |
196 |
Из табл. 1 видно что при повышении температуры увеличивается предельное напряжение сдвига, это связано с интенсификацией коагуляционного структурообразования. Объем жидкой фазы в системе увеличивается, так как растворимость сахарозы с увеличением температуры возрастает на 25 %, следовательно, пластичность при повышении температуры так же резко возрастает [3].
М.С. Белопольским было доказано, что чувствительность дисперсной массы к процессу сушки можно описать с помощью коэффициента образования поверхностных трещин в момент усадки поверхностного слоя и коэффициента образования внутренних трещин в период окончания усадки поверхностного слоя.
Математическое описание процесса сушки с помощью системы дифференциальных уравнений тепловлагопереноса имеет ряд сложностей, в этой связи для описания процесса сушки используют критерии подобия тепломассопереноса, среди которых можно выделить следующие: Лыкова (Lu), Поснова (Рп), Кирпичева (Ki), Вио (Bi), Коссовича (Ko), Фурье (Fo), Ребиндера (Rb) [3].
Проведя анализ коэффициента теплопроводности можно сделать вывод, что его величина не зависит от массы материала, а теплопроводность можно рассчитать также по правилу аддитивности. Согласно Киршеру коэффициент теплопроводности можно определять по следующему выражению [4]:
– при передаче тепла вдоль слоев
λсм = (1 – П) λт + Пλж, (4)
– при передаче тепла поперек слоев
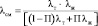 , (5)
, (5)
где П – пористость слоя материала;
λт, λж, λсм – коэффициенты теплопроводности твердой, жидкой фаз и их смеси.
В результате литературного обзора было выявлено большое количество различных зависимостей для определения коэффициента теплопроводности влажных дисперсных материалов, но в этих зависимостях не учитывается объемный фазовый состав. Зависимости являются эмпирическими и имеют узкий круг применения. Поэтому формула, предложенная Киршером, обладает преимуществом, т.к. учитывает объемное содержание жидкой и твердой фазы, но в этой формуле не учитывается объемное содержание газовой фазы, имеющей хоть и небольшую массу в системе, имея небольшую плотность и теплопроводность, она может оказывать существенное влияние на процесс сушки. Учитывая все вышесказанное, формула для расчета коэффициента теплопроводности дисперсных материалов будет иметь вид
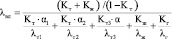 , (6)
, (6)
где λт, λж, λг, λвл – коэффициенты теплопроводности твердой, жидкой, газовой фаз и дисперсного материала;
α1, α2, α3 – коэффициенты объемной концентрации составляющих твердой фазы;
α1 + α2 + α3 = 1. (7)
Выражение в числителе формулы (6) учитывает соотношение всех трех фаз и при Кж = 0 трансформируется в соотношение твердой и газовой фаз.
Для подтверждения адекватности полученной формулы были проведены серии экспериментов для определения коэффициента теплопроводности на модельной смеси, имеющей состав: сахар – 60 %; крахмал – 25 %; шрот аронии – 15 %; премиксы 0,01 (сверх 100 %). Результаты сведены в табл. 2.
Таблица 2
Теплофизические свойства влажной смеси
|
Waбc |
ρвл, кг/м3 |
ρcyx, кг/м3 |
Kт |
Кж |
Кг |
λвл,Вт/м*град |
свл, КДж/кг*град |
aвл*107, м2/с |
Ккп*106, м2/с |
Lu |
|
0,051 |
1235 |
1156 |
0,630 |
0,079 |
0,290 |
0,140 |
1,150 |
0,206 |
– |
– |
|
0,082 |
1336 |
1205 |
0,650 |
0,131 |
0,220 |
0,208 |
1,313 |
0,253 |
– |
– |
|
0,100 |
1474 |
1304 |
0,690 |
0,170 |
0,140 |
0,376 |
1,510 |
0,369 |
– |
– |
|
0,121 |
1587 |
1373 |
0,718 |
0,214 |
0,068 |
0,758 |
1,566 |
0,676 |
– |
– |
|
0,142 |
1687 |
1328 |
0,740 |
0,260 |
– |
1,883 |
1,709 |
1,466 |
0,000 |
0,00 |
|
0,158 |
1647 |
1368 |
0,716 |
0,279 |
0,005 |
2,028 |
1,774 |
1,550 |
0,046 |
0,30 |
|
0,181 |
1612 |
1304 |
0,690 |
0,308 |
0,002 |
1,999 |
1,870 |
1,475 |
0,113 |
0,76 |
|
0,198 |
1576 |
1250 |
0,670 |
0,327 |
0,003 |
1,822 |
1,934 |
1,324 |
0,162 |
1,22 |
|
0,218 |
1536 |
1190 |
0,644 |
0,347 |
0,009 |
1,453 |
2,002 |
1,041 |
0,221 |
2,12 |
|
0,236 |
1491 |
1130 |
0,620 |
0,361 |
0,019 |
1,102 |
2,051 |
0,789 |
0,273 |
3,46 |
|
0,252 |
1445 |
1074 |
0,597 |
0,372 |
0,031 |
0,844 |
2,090 |
0,607 |
0,319 |
5,25 |
|
0,275 |
1378 |
995 |
0,565 |
0,383 |
0,052 |
0,582 |
2,130 |
0,426 |
0,386 |
9,06 |
|
0,297 |
1306 |
916 |
0,533 |
0,391 |
0,076 |
0,415 |
2,161 |
0,312 |
0,450 |
14,42 |
|
0,319 |
1258 |
857 |
0,509 |
0,401 |
0,090 |
0,346 |
2,196 |
0,263 |
0,514 |
19,54 |
|
0,335 |
1182 |
785 |
0,480 |
0,397 |
0,123 |
0,249 |
2,188 |
0,200 |
0,561 |
28,05 |
Коэффициент теплопроводности у сухих монолитных образцов размерами 50х50х75 мм определялся методом постоянного плоского источника тепла. Образцы были изготовлены с помощью метода пластичного формования, влажность составляла 15 %, давление прессования 50 МПа. После прессования образцы подвергались сушке в сушильном шкафу при температуре 60 °С. Температура поддерживалась постоянной в течение всего процесса, после высушивания образцы охлаждались в эксикаторе до температуры 20 °С в течение 24 часов. Коэффициент теплопроводности смеси определялся экспериментальным путем и составлял в среднем 0,696 Вт/м·град. По формулам (4), (5) были рассчитаны коэффициенты теплопроводности и теплоемкости смеси во влажном состоянии. Данные для этих расчетов принимались согласно значениям, полученным расчетно-экспериментальным путем во время предварительных исследований. Влагапроводность смеси рассчитывалась по коэффициенту капиллярной пропитки Ккп (м2/с) по следующему выражению:
W = 0,344•106 Kкп + 0,142, (8)
Kт = – 0,52•Kкп + 0,74. (9)
Результаты исследования и их обсуждение
Согласно полученным данным (табл. 2) при влажности Wнкв = 0,142, коэффициент капиллярной пропитки равен нулю, данную влагу, возможно, удалить во время термического обезвоживания, поэтому критерий Лыкова может быть определен при условии W > Wнкв, т.е. когда образуется капилярно подвижная влага. При влажности 19 % обеспечивается равновесная скорость изотермической и изоконцентрационной поверхностей. При влажности W > 0,19 коэффициент Лыкова равен Lu > l. Этот процесс сушки наиболее опасен, так как сушка материала будет идти с постоянной скоростью, а скорость диффузии влаги будет превышать скорость диффузии тепла. Поэтому при перемещении капиллярно-подвижной влаги температура в центре гранулы будет ниже температуры сушильного агента. После окончания процесса перемещения и удаления капиллярно-подвижной влаги температура материала будет повышаться, так как будет происходить углубленное испарение, то есть в процессе начинает преобладать температуропроводность.
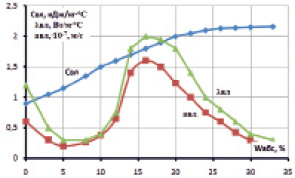
Теплофизические свойства материала в зависимости от его влагосодержания
Согласно рисунку теплоемкость исследуемой смеси увеличивается до оптимальной формовочной влажности W = 0,24. При влажности 0,24–0,335 теплоемкость смеси практически не изменяется, несмотря на изменение фаз системы. Это объясняется тем, что увеличение влагосодержания материала происходит более интенсивно за счет изменения объемной концентрации жидкой фазы по сравнению с объемной концентрацией твердой фазы в связи с существенным различием плотностей этих двух фаз. Из графика видно, что при высокой влажности гранулы имеют высокое термическое сопротивление, но при достижении влажности 10–12 % происходит резкое возростание теплопроводности. При этом коэффициент теплопроводности для данной влажности превышает для всех фаз, из которых состоит материал. Это связано с высокой теплопроводностью влажных материалов.
Выводы
В результате проведенных исследований можно сделать вывод, что для совершенствования методики определения теплофизических характеристик дисперсных систем необходимо использовать фазовые объемные характеристики, что в конечном итоге позволит повысить достоверность полученных результатов. Использование этих характеристик может позволить более подробно понять механизм аномально высокой теплопроводности влажных материалов и в дальнейшем прогнозировать не только изменения теплофизических свойств, но и поведение материалов во время проведения процесса при различных значениях содержания фаз.
Библиографическая ссылка
Попов А.М., Доня Д.В., Кравченко С.Н., Плотникова И.О., Плотников К.Б., Хлопотов И.В. ИЗМЕНЕНИЕ ФАЗОВЫХ ХАРАКТЕРИСТИК ВЛАЖНЫХ ДИСПЕРСНЫХ СИСТЕМ // Фундаментальные исследования. 2016. № 11-2. С. 318-322;URL: https://fundamental-research.ru/ru/article/view?id=40973 (дата обращения: 30.01.2026).



