Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кондратьев А.С. 1 Ньа Т.Л. 1 Швыдько П.П. 1

---

1 Московский политехнический университет

Показано, что разброс опытных данных по величине коэффициента гидравлического сопротивления связан с использованием в качестве характерного размера эквивалентного диаметра частиц по объему, вместо эквивалентного гидродинамического диаметра, определяемого по площади боковой поверхности частицы и её миделевому сечению. Для учета влияния несферичности частиц на величину коэффициента гидравлического сопротивления вводится динамический коэффициент формы частицы, для определения которого, при различных режимах обтекания, используются три различные эмпирические зависимости. На основе анализа опытных данных и известных эмпирических зависимостей предложена единая обобщенная формула расчета коэффициента гидравлического сопротивления при свободном движении частиц произвольной формы в процессе осаждения и при гидротранспортировании в виде взвеси. Полученная зависимость позволяет рассчитать коэффициент сопротивления сферы и частиц произвольной формы при ламинарном, переходном и турбулентном режимах обтекания твердых частиц.

Статья в формате PDF

0 KB

коэффициент гидравлического сопротивления

монодисперсные частицы произвольной формы

1. Великанов Н.Л., Наумов В.А., Примак Л.В. Осаждение части ц взвесей в воде // Механиз. строит. – 2013. – № 7 (829). – С. 44–48.

2. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. Под ред. М.О. Штейнберга. – М.: Маш., 1992. – 672 с.

3. Кондратьев А.С. Осаждение полимодальных твердых частиц в ньютоновских жидкостях. – М.: Спутник+, 2014. – 121 с.

4. Кондратьев А.С., Наумова Е.А. Простая приближенная формула для коэффициента сопротивления сферической частицы. Пробл. аксиомат. в гидрогаз. – М.: Век книги, 2002. – Вып. 10. – С. 39–43.

5. Масюткин Е.П., Просвирин В.И., Авдеев Б.А. Влияние формы золей на эффективность очистки дисперсных сред // Вост. – Европ. жур. перед. технол. – 2012. – Т. 5/8 (59). – С. 52–57.

6. Наумов В.А. Зависимость силы гидродинамического сопротивления твердых частиц от показателей несферичности // Вестн. науки и образ. Сев.-Зап. России. – 2015. – Т. 1, № 1. – 10 с. [интернет ресурс: http://vestnik-nauk.ru].

7. Новый справочник химика и технолога. Процессы и аппараты химических технологий. Ч. II. (Г.М. Островский, Р.Ш. Абиев, В.М. Александров и др.; под ред. Г.М. Островского, Е.В. Иванова, Ю.П. Удалова и др. – СПб.: НПО «Профессионал», 2006. – 916 с.

8. Райст П. Аэрозоли. Введение в теорию. – М.: Мир. 1987. – 280 с.

9. Циборовский Я. Основы процессов химической технологии. – Л.: Химия. 1967. – 719 с.

10. Шлихтинг Г. Теория пограничного слоя. – М.: Наука, 712 с.

11. Cheng N.S. A simplified settling velocity formula for sediment particle // J. Hydra. Engin. ASCE. – 1997. – V. 123 (2). – P. 149–152.

12. Zhiyao S., Tingting W., Fumin X., Ruijie L. A simple formula for predicting velocity of sediment particles // Wat. Scien. & Engin. – 2008. – V. 1. – № 1. – P. 37–43.

Расчет коэффициента сопротивления при осаждении монодисперсных твердых частиц произвольной формы периодически обсуждается в современной научно-технической литературе см., например [4/6, 11, 12]. Как правило, исходными для последующего анализа являются классические опытные данные по коэффициенту гидравлического сопротивления сферической частицы и цилиндра, приведенные, например, в [10].

В работе [5] отмечается, что согласно существующей классификации [8] частицы различной формы разделяются на три основных класса.

1. Частицы, у которых все три измерения имеют примерно одинаковую величину (сферы, правильные многогранники и т.п.).

2. Частицы, имеющие в двух измерениях значительно большую протяженность, чем в третьем (диски, чешуйки и т.п.).

3. Частицы протяженные в одном направлении и имеющие сравнительно небольшие размеры в двух других (призмы, иглы, волокна и т.п.).

При этом в [5] под эквивалентным (эффективным) диаметром частицы понимается диаметр сферической частицы, которая также взаимодействует с окружающей средой, как и рассматриваемая частица [7]. Уточним, что под понятием одинакового взаимодействия могут пониматься различные процессы. Например, в гидромеханике осаждения это скорость осаждения твердой частицы. При наличии процесса химического реагирования материала частиц с компонентами несущей среды одинаковое взаимодействие это масса прореагировавшего вещества, которая связана со временем пребывания частиц в реакторе и реакционной поверхностью частиц. Поэтому понятие эффективного (эквивалентного) диаметра частицы произвольной формы определяется результатом конкретных процессов её взаимодействия с окружающей средой, а не только её формой.

Для учета влияния формы частицы на её гидравлическое сопротивление используется так называемый фактор (коэффициент) формы частицы ψ, который определяется как отношение поверхности сферы (Ss) к поверхности частицы (Sp) того объема (Vs = Vp), по формуле Ваделла [8, 9]:

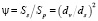
(при условии, что Vs = Vp), (1)

где Vs и Vp – объем сферы и частицы, соответственно; dv – диаметр сферы, имеющий тот же объем, что и частица; ds – диаметр сферы, имеющий туже боковую поверхность, что и поверхность частицы равного объема.

В иностранной литературе используется приведенное определение фактора формы частицы ψ. Величина обратная фактору формы 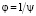называется коэффициентом несферичности или угловатости. В отечественной литературе (см., например, [6]) иногда под понятием коэффициента формы или коэффициента несферичности частицы понимается обратная величина .

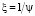Поскольку при фиксированном объеме шар имеет минимальную поверхность, то величина ψ ≤ 1. При расчете эквивалентных диаметров, приведенных в табл. 1, предполагалось, что объем куба равен 1 единице объема; у параллелепипедов указано отношение ребер; у конуса диаметр основания равен высоте; у усеченного конуса диаметр нижнего основания равен 2 (единицам длины), а высота и диаметр верхнего основания равны 1 (единице); у прямоугольной пирамиды высотой 1 в основании квадрат со стороной 1; и усеченной прямоугольной пирамиды высотой 1 в основании квадрат со стороной 1, а в верхнем основании квадрат со стороной 0,5; у треугольной пирамиды высотой 1 в основании правильный треугольник со стороной 1; у усеченной треугольной пирамиды высотой 1 в основаниях правильные треугольники со сторонами 1 и 0,5 [5].

Таблица 1

Значения эквивалентных диаметров частиц

В табл. 1 приведены значения эквивалентных диаметров для частиц простой геометрической формы [5], дополненные расчетной величиной de.

Сила гидравлического сопротивления жидкости при обтекании частицы определяется по стандартной формуле

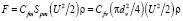, (2)

где Spm – поперечное (миделево) сечение частицы, то есть максимальное поперечное сечение перпендикулярное относительно направления движения частицы; Cfm – коэффициент гидравлического сопротивления, отнесенного к диаметру dm; Cfv – коэффициент гидравлического сопротивления, отнесенного к диаметру dv; U – скорость движения частицы; ρ – плотность жидкости.

При известном значении коэффициента гидравлического сопротивления Cfm или Cfv расчет скорости свободного осаждения твердых частиц проводится путем приравнивания силы гидродинамического сопротивления (2) разности силы веса частицы и силы Архимеда. В работах [5, 11, 12], по умолчанию, предполагается, что для песчинок выполняется условие dm = dv. Из данных приведенных в табл. 1, следует, что величина отношения (dm/dv), в зависимости от геометрической формы частиц, может быть как больше, так и меньше единицы. В работе [4] во всех случаях скорость осаждения рассчитывалась с использованием в выражении (2) величины Cfm. В работах [1, 5, 6] прямо указывается, что площадь наибольшего (миделевого) сечения частиц принимается равной площади сферической частиц, определенной по величине dv. Для сравнительной оценки рассматриваемых методов расчета коэффициента гидравлического сопротивления вначале будем придерживаться представления, что dm ≈ dv.

Рассмотрим движение несферических частиц при больших числах Рейнольдса. Как показывают опытные данные [2], в этом случае величина коэффициента гидравлического сопротивления изменяется в небольших пределах, например для тел с острой кромкой (пластины: круглая, квадратная, прямоугольная и т.п.) коэффициент гидравлического сопротивления находится в пределах 1,1/1,3.

Поскольку большей частью форма измельченных твердых материалов весьма значительно отличается от сферической или цилиндрической, для расчета их коэффициентов гидравлического сопротивления предлагались различные эмпирические зависимости. Так в работе [11] при перекачке водо-песчаных смесей использована следующая зависимость для коэффициента гидравлического сопротивления Cfv

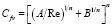, (3)

где 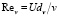– число Рейнольдса, определенное по скорости движения (свободного осаждения) частицы U и эквивалентному диаметру dv – диаметру сферической частицы, объем которой равен фактическому объему частицы произвольной формы; ν – кинематическая вязкость несущей жидкости; A, B и n – постоянные, подбираемые из условия наименьшего расхождения с опубликованными в литературе опытными данными. Результаты расчетов сравнивались также с шестью известными эмпирическими зависимостями других авторов, предложенными в 1954–1993 гг.

Из приведенных в работе [11] данных следовало, что при низком значении числа Rev, когда вторым членом в квадратных скобках в правой части формулы (3) можно пренебречь, принято значение A = 34. В другом предельном случае при высоком значении числа Rev >> 1, когда можно пренебречь первым членом в квадратных скобках в правой части формулы (3), принято значение B = 1, хотя в анализируемых данных среднее значение B = 1,1. Величина показателя степени n = 1,5. Используя указанные значения эмпирических постоянных, в [11] получено следующее выражение:

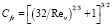. (4)

В работе [4], в дополнение к эквивалентным диаметрам dv, ds и dm для частиц произвольной формы, вводился эквивалентный гидродинамический диаметр частицы de

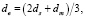(5)

который используется для вычисления числа Рейнольдса 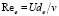. Последнее соотношение (5) обосновывается тем, что в случае сферической частицы две трети общего гидравлического сопротивления определяются силой гидравлического трения о внешнюю поверхность частицы, а одна треть определяется разностью силы давления в лобовой и в кормовой областях сферической частицы, то есть перепадом давления в плоскости медианного сечения. Во всех случаях сила сопротивления не отличалась более чем на 8 % от точных численных значений, что подтверждало приемлемость сформулированного выше подхода [4].

Для коэффициента гидравлического сопротивления используется интерполяционная зависимость [4]

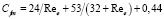. (6)

Последнее выражение при Ree ≤ 2×104 согласуется с экспериментальной зависимостью для коэффициента гидравлического сопротивления шара с погрешностью менее 5 % [3].

В работе [12] значения эмпирических коэффициентов A, B и n, входящих в выражение (3), также подбирались путем анализа опытных данных частиц двух видов: сфер и песчинок. В табл. 2 приведен диапазон используемых значений этих величин по данным девяти опубликованных источников.

Таблица 2

Значения диапазона коэффициентов в (3) по данным [12]

Далее использовалось выражение (3), в котором значения коэффициентов A, B и n подбирались и сравнивались с опытными данными и расчетами по эмпирическим зависимостями других авторов, опубликованными в 1993–2005 гг. По результатам такого сопоставления было получено, что зависимость (1) при A = 32,2, B = 1,17 и n = 1,75 обеспечивает лучшее соответствие с опытными данными, в сравнении с зависимостями других авторов. В окончательном виде выражение для коэффициента гидравлического сопротивления записывается как

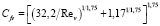. (7)

Сопоставление с опытными данными по скорости свободного осаждения песчаных частиц показало, что расхождение между расчетными и опытными значениями скорости составляет ± 25 % [12], то есть достаточно значительно.

В работе [6], при анализе влияния несферичности частиц на коэффициент гидравлического сопротивления, автор использует выражение

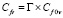, (8)

где Γ – динамический коэффициент формы, зависящий от фактора формы частицы ψ, а Cf0v – зависимость коэффициента сферической частицы от числа Рейнольдса, в качестве которой используется выражение

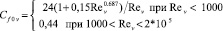. (9)

Отметим, что для сферических частиц dm = dv, а значит, Cf0m = Cf0v.

Выполненный автором [6] анализ показал, что при небольших числах Рейнольдса величина Γ может рассчитываться по зависимости

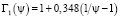. (10)

Сравнение зависимости (10) с эмпирическими зависимостями других авторов [6], показало, что в (10) не учтено влияние числа Рейнольдса. Однако приведенный разброс экспериментальных данных величин динамического коэффициента формы 0,6 ≤ Γ1 ≤ 1,4 (± 40 % от 1) при малых числах Рейнольдса 7×10-7 < Rev < 7×10-1 настолько велик, что не позволяет сделать вывод о наличии зависимости Γ1 от числа Рейнольдса.

При достаточно больших числах Рейнольдса Rev = 2×103÷2×105 величина Γ может рассчитываться по линейной зависимости

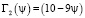. (11)

Эмпирические зависимости других авторов при Rev = 105 согласуются с расчетом по формуле (11) [6]. Для проведения расчета динамического коэффициента формы в переходной и квадратичной областях сопротивления, в качестве первого приближения, рекомендуется следующая совокупность соотношений. При Rev < 0,2 рекомендуется использовать формулу (10). При Rev > 1162 рекомендуется использовать формулу (11). В промежуточной области чисел Рейнольдса 0,2 ≤ Rev ≤ 1162 рекомендуется следующая зависимость

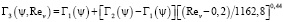. (12)

На рис. 1 показана зависимость динамического коэффициента формы Г от числа Рейнольдса частиц песка в линейной, переходной и квадратичной областях сопротивления, рассчитанная по формуле (12). В расчетах принято, что для частиц песка ψ = 0,813. Здесь же нанесены опытные значения Γ(ψ, Rev), которые приведены в работе [6]. Сравнение опытных и расчетных данных показывает, что расхождение между ними не превышает 36 %.

Покажем, что аналогичный результат может быть получен без привлечения дополнительной эмпирической зависимости (12). Используя выражение (6), в соответствии с определением динамического коэффициента формы Г по формуле (5) и привлекая выражение (10) для области малых чисел Рейнольдса и выражение (11) для области переходного и квадратичного режима сопротивления, запишем

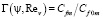, (13)

где

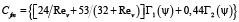; (14)

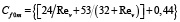. (15)

Сравнение опытных и расчетных по формуле (13) данных, представленное на рис. 1, показывает, что расхождение между ними несколько уменьшается по сравнению с расчетом по формуле (12).

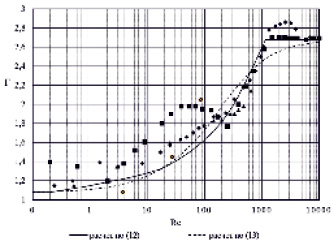
Рис. 1. Зависимость динамического коэффициента формы от числа Рейнольдса частиц песка в переходной и квадратичной области сопротивления

Проведем сравнение значений коэффициентов гидравлического сопротивления, рассчитанных по формулам (4), (7), совокупности формул (9)÷(12) и формуле (14). Для расчетов по последним формулам необходимо задание фактора формы частицы ψ. Анализ, проведенный в работе [6], показал, что точное численное значение ψ – достаточно неопределенная величина. Например, для зернистого (неокатанного) песка ψ = 0,667. Отметим, что то же значение ψ имеется у треугольной пирамиды с определенным соотношением сторон треугольника в основании и высотой пирамиды (см. табл. 1). В других условиях, возможно связанной с особенной формой песчинок, получено, что ψ = 0,521 [6]. Последнее значение не соответствует ни одному из видов частиц рассмотренных в табл. 1. Поэтому в расчетах было приято значение ψ = 0,667.

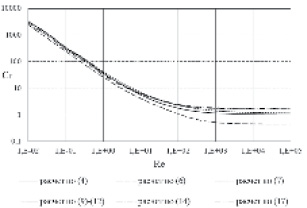
Рис. 2. Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса

На рис. 2 показаны четыре расчетные кривые, рассчитанные по формулам: (4) – 1, (7) – 2, (9)÷(12) – 3 и (14) – 4. Можно констатировать, что расхождения от среднего между расчетными зависимостями не превышают 10 %, что представляется неплохим результатом. Первые две зависимости являются чисто эмпирическим. В методе расчета, изложенном в работе [6], используется пять эмпирических зависимостей. При расчете по формуле (14) используются три эмпирические зависимости (6), (9) и (10), причем приемлемость формулы (6) была ранее подтверждена на обширном экспериментальном материале по осаждению моно- и полидисперсных частиц несферической формы и различной плотности при свободном и стесненном осаждении с объемным содержанием твердой фазы до 0,5 [3]. Дополнительно на рис. 2 нанесена кривая, рассчитанная для частиц сферической формы по формуле (6). Из графиков видно, что зависимость (14) позволяет рассчитывать коэффициент гидравлического сопротивления как шара зависимости (14) при (ψ = 1), так и тел произвольной формы.

Из формулы (2) следует, что

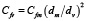. (16)

Для расчета величины Cfm можно использовать выражение (14). Если предварительно исключить из рассмотрения частицы имеющие форму конуса, прямоугольной пирамиды и параллелепипеда со сторонами 1×2×2, как маловероятные, величина отношения 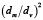по данным, приведенным в табл. 1, находится в пределах 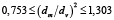. В этом случае практически все расчетные значения коэффициента гидравлического сопротивления, определяемые зависимостью (16), и опытные значения находятся в пределах, не превышающих 36 % от среднего значения при .

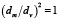Возможно также использование зависимости подобной (14), в которой отсутствуют эмпирические зависимости для Γ1(ψ) и Γ2(ψ). Проведем расчет коэффициента гидравлического сопротивления с использованием выражений (2), (5) и (6). Конечное выражение для величины Cfv представим в виде

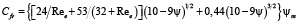. (17)

В соответствии с выражением (5), связь между числами Рейнольдса Ree и Rev определяется соотношением

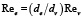. (18)

В выражении (17) множитель ψm =(dm/dv)2 учитывает, что площадь миделева сечения частицы отличается от диаметра поперечного сечения шара, равного по объему частице. Как показали поверочные расчеты, поправочная функция (11), представленная в виде степенной зависимости (10 – 9×ψ)n при различных показателях степени n = 1/2 и 3/2 может использоваться в качестве поправочного коэффициента для расчета коэффициента гидравлического сопротивления как при малых числах Рейнольдса, так и при больших числах Рейнольдса соответственно.

На рис. 2 видно, что зависимость, рассчитанная по формуле (17), фактически близка к «среднему» значению, коэффициента гидравлического сопротивления, по отношению к другим зависимостям, что позволяет рекомендовать её для использования в инженерных расчетах. В расчетах использовались величины, характеризующие частицы кубической формы (см. табл. 1) dv = 1,241; ds = 1,382; dm = 1,128; de = 1,297; ψ = 0,806 и ψm = 0,827, которые, как представляется, по геометрической форме наиболее близки к частицам песка.

Проведенный анализ показал следующее.

Причиной значительного разброса опытных данных и их значительное отличие от расчетных значений, в том числе, и эмпирических зависимостей, связано с тем, что в качестве характерного размера используется эквивалентный диаметр dv.

При свободном обтекании частиц число Рейнольдса определяется величиной эффективного гидравлического диаметра de.

Учет этих факторов позволил получить новую эмпирическую зависимость (17) для расчета коэффициента гидравлического сопротивления твердых частиц произвольной формы.

Библиографическая ссылка