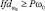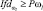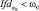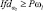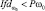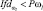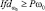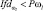Министерство здравоохранения РФ определило в качестве одного из приоритетных направлений развития концепции повышения качества и результативности медицинского обслуживания населения (особенно в области профилактики и лечения социально значимых заболеваний) интенсивную разработку и экстенсивное внедрение современных информационных технологий и иных инноваций в области своевременной и ранней диагностики на основе скрининга, превентивной медицины и профилактических мероприятий [29].
Современные медицинские системы поддержки принятия решений основываются на достижениях компьютерных технологий в области искусственного интеллекта и системного анализа [1, 18, 23, 31]. Основой медицинских приложений методологии системного являются фундаментальные работы, основанные на богатом экспериментальном материале, в области теорий функциональных систем организма и биотехнических систем, созданные и постоянно актуализируемыми российскими учеными П.К. Анохиным, В.М. Ахутиным, Е.П. Попечителевым, Н.А. Кореневским, К.В. Судаковым [3, 15, 16, 24, 25, 28, 30].
Согласно концепции системного подхода, как патологические, так и нормальные состояния организма характеризуются численными, логическими и-или семантическими значениями информативных наблюдаемых (регистрируемых) и-или регулируемых параметраов (показателей, характеристик), образующих определенную, специфическую для диагностируемого состояния, структуру. (Вопросам формирования репрезентативного множества информативных показателей на основе анализа самоорганизационных моделей структуры данных с учетом специфики биологических объектов посвящены, например, работы [27, 33].)
Изменение структуры регистрируемых показателей по сути является индикатором диагностируемых состояний организма, соответствующим определенным патологиям (или нозологиям) [7]. Формализованное определение значения подобных индикаторов происходящих в организме системных изменений позволяет реализовать базу знаний в автоматизированной системе поддержке диагностических решений с приемлемым для медиков-клиницистов качеством функционирования. Численные значения индикаторов и определение значимых пороговых диапазонов соответствия определенным кластерам состояний позволяют применять их в качестве аргументов продукционных решающих правил как четкого, так и нечеткого логического выводов.
СППДР в силу доминирования идеологии экспертных систем применяются не столько в индивидуальном лечении, сколько на этапах превентивной медицины, работы консилиумов, повышения квалификации медицинских работников (в качестве интеллектуальных тренажеров) [8, 10, 32], несмотря на то, что когнитологи при их создании используют знания высокопрофессиональных экспертов и-или клинически подтвержденной информации, извлеченных из литературных источников и медицинских баз данных [35].
В процессе обучения автоматизированной системы формируется информативное для каждой нозологии множество параметров, на основании анализа которых может осуществляться рекомендательная превентивная диагностика на основе идентифицированных выработка диагностических правил и функций-аргументов к ним. Для этого применяется алгоритм, который состоит из следующих этапов [4, 8]:
а) Нормирование показателей, которое заключается в алгебраическом делении значения показателя на «норму», – рекомендуется модальное значение конкретного показателя в группе здоровых (не больных) людей. Для определения целесообразности использования параметрических методов определяют тип распределения каждого из исследуемых параметров, используя, например, тесты Колмогорова – Смирнова, Шапиро – Уилки и хи-квадрат.
б) Проведение регрессионного анализа (линейного, нелинейного, парного, множественного). Идентифицируются приемлемо статистически значимые функциональные зависимости для каждой нозологии.
в) На экзаменационной выборке синтезируются решающие диагностические правила (чаще всего – продукционного типа).
г) Диагностика состояния пациента после проведения необходимых лабораторных исследований и регистрации значений, применяемых в диагностических правилах показателей, осуществляется следующим образом: по идентифицированным уравнениям оценивается средняя квадратичная ошибка – отклонение реального значения регистрируемого показателя от расчетного (среднее значение и вариационный размах ошибки) [22]. Для каждого альтернативного класса ωk рассчитываются значения меры (критерия) дальности множеств по формуле:
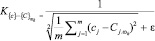, (1)
где m – количество моделей аппроксимантов в классе ωk (не превышает количество регистрируемых показателей), ε – вычислительная точность, cj – значение показателя j регистрируемого у пациента,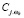 
– значение показателя j в классе ωk, вычисленное согласно идентифицированным функциональным зависимостям – аппроксимантам.
Далее вычисляем коэффициент уверенности меры дальности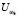 
, отражающей возможность принадлежности объекта исследования – пациента определенному альтернативному классу заболеваний печени и-или контрольной группе по формуле
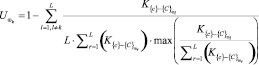, (2)
где L – количество альтернативных классов.
Диагностические заключения относительно порогов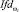 
|
|
|
|
|
Описание ситуации |
|
0 |
0 |
0 |
1 |
Здоров – класс ω0 |
|
0 |
0 |
1 |
0 |
Дополнительное обследование |
|
0 |
1 |
0 |
0 |
Болен – класс ωk1 |
|
1 |
0 |
0 |
0 |
Дополнительное обследование |
В качестве «индикатора функциональных различий» –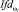 
, характеризующего отличие анализируемого состояния ωl от всех остальных рассматриваемых состояний (в разветвляющей вершине дерева решений дифференциальной диагностики), предлагается использовать формулу
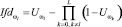. (3)
С целью учета «желаемых» взаимоотношений между значениями ошибок первого и второго рода принятие классификационных решений в СППДР может осуществляться с использованием двух порогов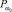 
и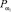 
, относительно которых строится таблица принятия решений. Если значение 
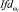не превышает значения порога 
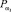, то элемент таблицы равен нулю. В противном случае – единице. Величины порогов 
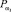определяются экспертами на этапе обучения.
В качестве предлагаемого решения, например, могут быть использованы заключения: «1 – Пациент нуждается в дополнительном обследовании»; «2 – Вероятность присутствия предполагаемой патологии (нозологии) низка»; «3 – Высока вероятность присутствия предполагаемой патологии (нозологии)».
Интегральные (латентные) показатели предлагается рассчитывать по методике, предложенной в [20, 21].
Значения интегральных показателей определяются по формуле
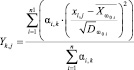, (4)
где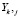 
– j – значение k-го интегрального показателя, 
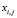– j-ое значение i-го частного показателя j, 
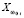– среднее значение i-го частного показателя в классе ω0, 
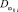– дисперсия i-го частного показателя, 
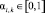– весовые коэффициенты, определяющие вклад показателя xi в формирование интегрального показателя Yk (определяются экспертами или на основе дисперсионного анализа или на основе иных статистических критериев [2, 22]).
д) Визуальное представление полученных результатов. Состояние организма (пациента) относится к тому кластеру, для которого его проекция в плоскости «среднее значение – вариационный размах» занимает более левое и нижнее положение (с предпочтением «левизны») или применяется продукционное правило:
Если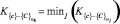 
, то состояние пациента соотносится с классом ωk с уверенностью 
,
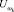или диагностика осуществляется в соответствии с таблицей.
В случае отсутствия пороговых значений (аналогичных представленным в таблице) предлагается применять следующее продукционное правило:
Если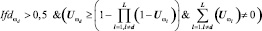 
.
то у пациента высока вероятность наличия состояния ωd.
Смысл последнего правила – состояние пациента соотносится к определенному классу, причем уверенность в соотнесении с ним должна превышать неуверенность принадлежности к другим, альтернативным в данном случае, заболеваниям печени. Назовем это правило – «альтернативным».
Поскольку в диагностической системе реализуется в данном случае несколько способов классификации, то, так как они не являются противоречивыми с точки зрения математической и семантической интерпретаций, предлагается использовать любой из них.
е) Коррекция базы знаний с учетом приемлемости результатов диагностики.
В процессе развития заболевания и-или проведения терапевтических процедур наблюдаются изменения состояний организма и, как следствие, структур и параметр, отражающих функциональные связи. Для выявления происходящих изменений школой А.В. Завьялова предлагается использовать Максимальный Градиент Функциональных Различий (the Maximum Gradient of the Functional Differences – MGFD), вычисляемый как наибольшее значение межранговых отклонений упорядоченных по убыванию значимых (приемлемых непротиворечивых) корреляций между показателями [9, 19, 20]. Показатель, имеющий наибольшую связность, рассматривается в дальнейшем как системообразующий для данного класса. Поскольку максимальное значение ранга равно (n – 1) (n – количество регистрируемых показателей), то индикатор корреляционных различий структур информативных показателей состояний организма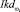 
предлагается вычислять по формуле
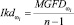. (5)
При сравнении биомедицинских сигналов (ЭКГ, ЭЭГ, ФПГ, дыхательные шумы и т.п.) в качестве меры связности между информативными характеристиками (показателями) сигналов предлагается использовать наряду с корреляцией значение когерентности и-или корреляции между спектральными функциями или иными хронометрическими показателями сигналов [5, 34].
Рассмотренная методология была успешно использована при построении решающих элементов систем поддержки принятия диагностических решений в следующих случаях:
– диагностика герпеса [26], рак желудка [12], заболевания печени [4, 20];
– анализ напряжения ФС человека-оператора (ЭВМ) [14];
– анализ экологической напряженности [13, с. 204–220];
– анализ здоровья новорожденного плода [11];
– анализ выбора учебной траектории абитуриентом [17].
В процессе дифференциальной диагностики на различных иерархических уровнях принятия решений в вершине принятия решений существуют альтернативы, количество которых характеризуют дуги, выходящие из вершин (минимальное количество – две). Каждая альтернатива имеет доминирование над остальными, которая может быть оценена с помощью некоторого «коэффициента парных различий» RPDk,l (k, l – индексы альтернативных решений). В этом случае каждая вершина графа принятия решений характеризуется матрицей предпочтений и выбор осуществляется автоматически с помощью методов и алгоритмов, основанных на «методе анализа иерархий», предложенном и достаточно хорошо разработанном в настоящее время Т. Саати [6].
Система поддержки принятия диагностических решений на каждом этапе последовательной дифференциации состояния автоматически или в интерактивном режиме с ЛПР (лицом, принимающим решение – в нашем случае – медицинским работником) осуществляет выбор на основании вектора предпочтений, полученного по матрице RPD либо методом средних геометрических либо путем вычисления главных собственных векторов указанной матрицы (в первом методе наблюдается в большинстве случаев нормального распределения высокая погрешность).
Элементы матрицы RPD Т. Саати предлагает определять экспертным путем (с учетом конкордации) или с использованием результата частотного анализа возникновения альтернативных ситуаций. Данные варианты требуют выполнения базовых постулатов доказательной медицины [22], которые часто трудно соблюсти в случае проектирования базы знаний СППДР с большим количеством разнообразных патологических состояний и иерархических уровней дерева принятия решений.
В связи с этим предлагается вычислять элементы матрицы RPD по рассмотренным индикаторам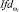 
и 
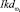следующим образом (учитывая, что их значения лежат в интервале [0, 1] и обладают метрическими свойствами).
В классическом варианте при одном виде критерия для выбора альтернатив элементы матрицы предпочтений связаны между собой следующим образом:
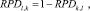
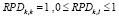. (6)
Рассмотрим случай, когда возникает необходимость применения некоторого множества различных (желательно семантически не связанных) критериев (the criterion of selection of alternatives) {CSA}NA, где NA – количество альтернатив. В случае применения концепции самоорганизационного моделирования (а именно ее настоятельно рекомендуется применять при исследовании систем организма человека, поскольку она наилучшим образом отражает сущность функционирования живых систем), множество {CSA}NA можно разделить на две группы: критерии внутренние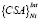 
и внешнего дополнения 
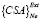(Ni + Ne = NA. Первые определяются на обучающей выборке, вторые на контрольной (выборки обладают свойствами репрезентативности ко всему множеству и между собой). Тогда элементы матрицы {RPD} формируются по следующим вариантам, в зависимости от цели исследований и предпочтений лица принимающего решения:
1. Элементы матрицы предпочтений вычисляются по формуле
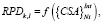
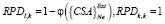. (7)
Далее определяется вектор собственных значений матрицы, по которому осуществляется формирование рекомендаций по диагностическому выбору.
Назовем данный способ «стратегией поликритериального внешнего дополнения».
В данном случае элементы матрицы предпочтений под главной диагональю представляют собой значения некоторых функций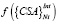 
свертки «внутренних» критериев, определяющих степень уверенности в том, что решение (диагноз) k предпочтительнее решения (диагноза) l в вершине иерархического дерева, идентифицированные на обучающей выборке. Значения элементов над главной диагональю определяются функциями 
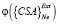свертки критериев внешнего дополнения, определяющих степень аналогичные степени уверенности, полученные на дополнительной (экзаменационной) выборке. Заметим, что если множества «внутренних» и «внешних» критериев идентичны, функции 
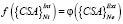, и обучающие и экзаменационные выборки подобны и репрезентативны относительно общего распределения и друг друга, то матрица {RPD} представляет собой классическую матрицу предпочтений в методе анализа иерархий [27].
2. Элементы матрицы предпочтений вычисляются по формуле
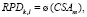
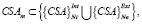
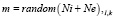. (8)
.
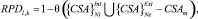
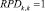Далее определяется вектор собственных значений матрицы, по которому осуществляется формирование рекомендаций по диагностическому выбору.
Назовем данный способ «стратегией полного внешнего дополнения».
В этом случае элементы под главной диагональю определяются с помощью некоторой функции ψ(CSAm) от любого элемента критерия выбора альтернатив CSAm, выбранного случайным образом из всех критериев, а остальные считаются внешним дополнением, над которыми для определения уверенности в предпочтении используется функция
.
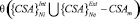3. Способ «итерационного поликритериальной стратегии»: элементы матрицы предпочтений формируются с помощью последовательных итерационных шагов:
1) Выбирается случайным образом любая функция ψ(CSAm), которая определяет элементы под главной диагональю, а функция (1 – ψ(CSAm)) определяет элементы над главной диагональю.
2) Определяется собственный вектор матрицы предпочтений W.
3) Строится новая матрица предпочтений {RPD}*, элементы которой являются разницами между соответствующими парами в собственном векторе: в случае положительной разницы – элементы под главной диагональю, отрицательной – над главой диагональю (по модулю). Не определенные элементы матрицы {RPD}* заполняются значениями соответствующих функций уверенности в предпочтениях, аналогичных случаю 1 (в качестве аргументов используются один или несколько CSA, выбранных случайным образом из оставшихся.
4) Если множество выбранных критериев не исчерпано, то п. 2–3 повторяются. Если исчерпано, то решение принимается согласно итоговому вектору W.
Таким образом, предлагаемые способы, несмотря на возрастание вычислительных затрат (особенно в третьем случае), позволяют существенно повысить качество принятия решений за счет использования принципа внешнего дополнения в методе анализа иерархий.
В случае использования двух критериев, например предлагаемых индикаторов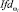 
и 
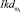процесс ранжирования рекомендательных диагностических решений дифференциального типа в каждой вершине графа представляет собой одношаговую процедуру (в итерационной поликритериальной стратегии – два шага, стратегии поликритериального и общего дополнения совпадают). В простейшем варианте рекомендуется использовать следующие функции:
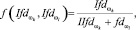
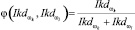. (9)
В случае отсутствия одного из индикаторов в формуле (10) он приравнивается нулю и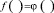 
.
Выводы
Поскольку развитие патологического процесса вызывает изменение состояний функциональных и физиологических систем, которые идентифицируются определенными структурами регистрируемыми управляемыми и-или наблюдаемыми показателями, то возникает возможность использования специальных индикаторов, отражающих корреляционно-функциональные различия между структурами, в алгоритмах дифференциальной диагностики, реализуемых в автоматизированных системах поддержки решений превентивной медицины в ходе скрининга приемлемого соотнесения состояния обследуемого к определенному заболеванию на ранней стадии.
Применение метода анализа иерархий, характерного для дифференциальной диагностики, совместно с методологией самоорганизационного моделирования при оценке исследуемого состояния к определенному кластеру и использованием критериев внешнего и внутреннего дополнения при построении матрицы предпочтений для вершин дерева принятия решений позволяет осуществлять классификационный процесс достаточными для автоматизации формализованными приемами, что приводит к повышению эффективности диагностического процесса в целом.
Учитывая актуальность и значимость проблем повышения качества и результативности диагностики социально значимых заболеваний на этапе массовой диспансеризации населения, предлагаемые в работе теоретические посылки требуют проведения дополнительных исследований на клиническом материале для удовлетворения постулатов доказательной медицины.
Библиографическая ссылка
Артеменко М.В., Добровольский И.И., Калугина Н.М., Писарев М.В. ИНДИКАТОРЫ ДИФФЕРЕНЦИАЛЬНОЙ ДИАГНОСТИКИ В СИСТЕМАХ ПОДДЕРЖКИ ПРИНЯТИЯ КЛАССИФИКАЦИОННЫХ РЕШЕНИЙ С ИСПОЛЬЗОВАНИЕМ МЕТОДА АНАЛИЗА ИЕРАРХИЙ // Фундаментальные исследования. – 2016. – № 11-1. – С. 15-22;URL: https://fundamental-research.ru/ru/article/view?id=40919 (дата обращения: 23.11.2024).