Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Котельников Е.В. 1

---

1 ФГБОУ ВО «Вятский государственный университет»

В статье рассматривается интеллектуальный анализ текстов на основе ДСМ-метода обнаружения эмпирических закономерностей, включающего процедуры индукции, аналогии и абдукции. В процедуре индукции порождаются гипотезы, которые затем применяются для классификации новых текстов и объяснения исходных данных в процедурах аналогии и абдукции. При этом возникают вычислительно сложные задачи с множествами гипотез и текстовых документов, которые сводятся к операции проверки включения одной гипотезы в другую гипотезу или в текст. В статье предлагается новый способ представления гипотез и документов на основе отсортированных списков целых чисел, упорядоченных по первому элементу. Эксперименты, проведенные с применением коллекций отзывов о фильмах, книгах и фотокамерах семинара РОМИП-2011, подтверждают эффективность разработанного способа, который на 12?% опережает по времени работы традиционные способы представления множеств.

Статья в формате PDF

0 KB

интеллектуальный анализ текстов

ДСМ-метод

представление гипотез

1. Белоусов А.И. Дискретная математика: учеб. для вузов / А.И. Белоусов, С.Б. Ткачев. – 3 е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 744 с.

2. Кормен Т.Х. Алгоритмы: построение и анализ / Т.Х. Кормен, Ч.И. Лейзерсон, Р.Л. Ривест, К. Штайн. – 3-е изд. – М.: ООО «ИД Вильямс», 2013. – 1328 с.

3. Котельников Е.В. Классификация отзывов о фильмах с использованием ДСМ метода / Е.В. Котельников // В мире научных открытий. – 2013. – № 6.1 (42). – С. 225–242.

4. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2000. – 304 с.

5. Финн В.К. Обнаружение эмпирических закономерностей в последовательностях баз фактов посредством ДСМ рассуждений // Научно-техническая информация. Сер. 2. – 2015. – № 8. – С. 1–29.

6. Bloom B.H. Space/Time Trade-offs in Hash Coding with Allowable Errors // Communications of the ACM. – 1970. – Vol. 13(7). – P. 422–426.

7. Chetviorkin I. Sentiment Analysis Track at ROMIP 2011 / I. Chetviorkin, P. Braslavskiy, N. Loukachevitch // Computational Linguistics and Intellectual Technologies: Papers from the Annual International Conference «Dialogue». – 2012. – № 11(18). Vol. 2. – P. 1–14.

8. Mining Text Data / Aggarwal C.C., Zhai C. (eds.), Springer, 2012. – 522 p.

Интеллектуальный анализ текстов (text mining) в настоящее время применяется во многих областях, таких как тематическая классификация веб-сайтов, анализ тональности отзывов о товарах и организациях, разработка диалоговых систем, ранжирование выдачи поисковых систем Интернета и др. [8]. При этом используются современные методы машинного обучения и интеллектуального анализа данных, например машины опорных векторов и нейронные сети. Одним из наиболее развитых подходов является ДСМ-метод обнаружения эмпирических закономерностей [5]. ДСМ-метод назван в честь английского философа, логика и экономиста Д.С. Милля (1806–1873) и включает три основные процедуры: индукцию, аналогию и абдукцию. В контексте интеллектуального анализа текстов при этом осуществляются следующие действия [3]: в процедуре индукции генерируются гипотезы о причинах свойств анализируемых текстов, например тематики или тональности; в процедуре аналогии эти свойства предсказываются для новых, ранее неизвестных текстов; в процедуре абдукции проверяется, объясняют ли сгенерированные гипотезы свойства исходных текстов.

Гипотеза представляет собой тройку, включающую фрагмент структуры текста (например, множество слов и словосочетаний), множество текстов, в которые входит данный фрагмент, и свойство, присутствующее у всех текстов предыдущего множества. В процедурах аналогии и абдукции должны быть реализованы различные действия с множествами текстов и гипотез, такие как формирование множества гипотез, соответствующих заданному тексту, или удаление гипотез, входящих в тексты с противоположными свойствами. Указанные действия основаны на операции проверки включения одной гипотезы в другую гипотезу или в текст, которая, в свою очередь, сводится к операции проверки включения множеств. Неэффективная реализация данной операции способна привести к невозможности использования ДСМ-метода для интеллектуального анализа в случае больших текстовых коллекций.

В настоящей статье предлагается структура данных, на основе которой возможна эффективная реализация операции проверки включения множеств, что подтверждается экспериментальным исследованием. При этом используются стандартные структуры данных языка C#.

Постановка задачи

Множество B есть подмножество множества A, если всякий элемент B есть элемент A [1, с. 33]. Также говорят, что B включено в A. При этом используется обозначение: B ⊂ A.

В работе рассматривается следующая постановка задачи: дано множество гипотез, представленных своими фрагментами, и множество текстов (или других гипотез). Требуется установить, является ли первое множество подмножеством второго (проверка включения множеств). При проверке включения используются только текстовые фрагменты гипотез.

Структуры данных

В работе были исследованы следующие структуры данных для представления гипотез и документов: хэш-таблицы, содержащие строки и целые числа, отсортированные списки строк и целых чисел, фильтры Блума.

1. Хэш-таблицы, хранящие строки

Хэш-таблица – это эффективная структура данных для реализации словарей [2, с. 285]. При представлении гипотезы (или документа) важен факт наличия или отсутствия во фрагменте, принадлежащем гипотезе, конкретного слова, поэтому все значения, хранящиеся во фрагменте, являются уникальными и для их представления может быть использована хэш-таблица. В языке C# хэш-таблица, хранящая строки, описывается следующим типом данных: HashSet<string>. Операция проверки включения одной хэш-таблицы в другую является для этого типа стандартной (IsSubsetOf).

2. Хэш-таблицы, хранящие целые числа

Обработка строковых переменных (тип string языка C#), в которых хранятся слова (словарные формы), может быть менее эффективной по сравнению с обработкой целочисленных переменных. Поэтому было рассмотрено представление слов при помощи целочисленных идентификаторов: каждое слово имеет уникальный идентификатор. Для отображения идентификатора в слово необходимо поддерживать ассоциативный массив, содержащий коллекцию пар <идентификатор, слово>. В языке C# хэш-таблица, хранящая целые числа, представляется типом данных HashSet<int>.

3. Отсортированные списки строк

Если хранить фрагменты гипотез (документы) в виде отсортированных списков слов (строк), то операцию проверки включения одного фрагмента в другой можно эффективно реализовать на основе алгоритма слияния [4, с. 30]: элементы списков последовательно сравниваются либо до конца наименьшего из списков, либо до первого несовпадения (модифицированный в работе алгоритм слияния, реализующий эту идею для целых чисел, приведен на рис. 1). При этом следует учитывать накладные расходы на сортировку элементов списков, но для быстрой сортировки (Quick Sort) [2, с. 198] такие расходы на практике оказываются невелики. Список строк в языке C# представляется типом данных List<string>.

4. Отсортированные списки целых чисел

В этой структуре данных объединены две ранее рассмотренные идеи: во-первых, представление слов в виде целочисленных идентификаторов, во-вторых, использование для хранения этих идентификаторов отсортированных списков (алгоритм слияния). Алгоритм проверки включения гипотез (документов) для такого представления приведен на рис. 1.

На C# тип данных для списка целых чисел выглядит следующим образом: List<int>.

5. Отсортированные списки целых чисел, упорядоченные по первому элементу

В работе предлагается новый способ представления множества гипотез (документов): каждая гипотеза (документ) хранится в виде отсортированного списка целых чисел (как и в предыдущем пункте), все гипотезы (документы) множества содержатся в коллекции списков; при этом списки в коллекции упорядочены по возрастанию первого элемента (см. рис. 2).

Такое представление позволяет реализовать эффективный алгоритм проверки включения множеств (рис. 3).

Рис. 1. Алгоритм проверки включения гипотез (документов)

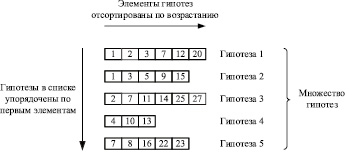
Рис. 2. Пример внутреннего представления гипотез (документов)

6. Фильтры Блума (Bloom filter)

Эта структура данных была предложена в 1970 г. Б. Блумом для компактного представления множеств на основе хэш-таблиц [6]. Для хранения данных используется битовый массив, а для представления элементов множеств в этом массиве применяется k хэш-функций, равномерно отображающих элементы на биты массива. При проверке присутствия элемента в фильтре Блума есть вероятность ложноположительного ответа, т.е. элемент отсутствует, а фильтр сообщает о его наличии; при этом ложноотрицательные ответы невозможны. Вероятность неправильного ответа прямо пропорциональна размеру битового массива и обратно пропорциональна количеству добавленных элементов. Для экспериментального исследования на языке C# был реализован класс BloomFilter.

У всех рассмотренных структур данных временная сложность операции проверки включения составляет в худшем случае O(N), поэтому для выбора наиболее эффективной структуры требуется проведение экспериментов.

Экспериментальное исследование

Экспериментальное исследование структур данных осуществлялось на основе текстовых коллекций отзывов о фильмах, книгах и фотокамерах семинара РОМИП-2011, подготовленных для задачи анализа тональности текстов [7]. При этом для позитивной и негативной тональностей в процессе индуктивного вывода были сгенерированы три пары множеств позитивных и негативных гипотез. Случайным образом из порожденных множеств для каждой предметной области были отобраны по 20 000 позитивных и 20 000 негативных гипотез.

Измерялось время проверки включения множества негативных гипотез в множество позитивных гипотез. Для каждой предметной области проводилось по пять тестов, результаты которых усреднялись. Затем вычислялось среднее время выполнения операции по всем трем предметным областям. Результаты экспериментов приведены в таблице.

Результаты экспериментального исследования структур данных для операции проверки включения множеств

Из таблицы видно, что наименьшее время работы оказывается в случае представления данных на основе отсортированных списков целых чисел, упорядоченных по первому элементу, с алгоритмом проверки включения множеств, приведенным на рис. 3. Отсортированные списки целых чисел заняли второе место с отставанием от лидера на 12 %. Существенно дольше работают структуры данных на базе хэш-таблиц (отставание от первых двух мест в 3–4 раза). Это связано с большим числом коллизий при хранении гипотез [2, с. 289]. Наконец, наибольшее время работы демонстрируют отсортированные списки строк и фильтры Блума. Для первой структуры данных причина невысоких результатов заключается в более высокой вычислительной сложности сравнения строк по сравнению с целыми числами. На продолжительности работы фильтров Блума негативно сказывается необходимость вычисления нескольких хэш-функций и разрешение ситуаций ложноположительных ответов.

Рис. 3. Алгоритм проверки включения множеств

Кроме перечисленных также исследовались другие структуры данных, входящие в состав языка C# и платформы .NET: BitArray, SortedSet<string>, SortedSet<int>, однако время их работы оказалось на порядок больше, чем у рассмотренных структур, поэтому в таблице они не представлены.

Заключение

В статье предложен новый способ представления гипотез и документов на основе отсортированных списков целых чисел, упорядоченных по первому элементу. Эксперименты, проведенные с применением коллекций отзывов о фильмах, книгах и фотокамерах семинара РОМИП-2011, подтвердили эффективность разработанного способа.

В перспективе планируется исследовать характеристики предложенного способа при параллельной реализации.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-07-00342а).

Библиографическая ссылка