Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Безуглов Д.А. 1 Юхнов В.И. 2

---

1 Ростовский филиал Российской таможенной академии

2 СКФ Московского технического университета связи и информатики

Одной из главных и наиболее сложных задач теории распознавания образов является выделение контуров объектов на изображении. На сегодняшний день эта задача актуальна, в том числе, например, при идентификации автомобиля по регистрационному номерному знаку. Сложность этой задачи связана с наличием цифровых шумов на входных изображениях, полученных в процессе их регистрации, оцифровки, а также в результате воздействия различных факторов. Реально существующие в настоящее время программы идентификации номерных знаков автомобилей предъявляют очень жесткие требования к качеству получаемых изображений. При настройке источника видеосигнала должно быть обеспечено качество изображения, пригодное для последующего анализа: номерной знак должен иметь высокую четкость и контрастность, изображение должно иметь широкий динамический диапазон яркости и не должно содержать сильных шумов. Выполнение этих требований в реальных условиях не всегда возможно. Поэтому в сложных условиях наблюдения существующие системы оказываются неработоспособны. Предложенный метод обработки изображений позволяет эффективно идентифицировать номерные знаки автомобилей, искаженные шумом.

Статья в формате PDF

0 KB

компьютерное зрение идентификация номерных знаков

вейвлет-дифференцирование

выделение контуров изображений

1. Безуглов Д.А. Оценка эффективности градиентного алгоритма стохастической аппроксимации в условиях воздействия шумов // Автоматика и вычислительная техника.- 1996. – № 4. – С. 15–23.

2. Безуглов Д.А. Кумулянтный метод оценки эффективности сегментированного зеркала адаптивной оптической системы // Оптика атмосферы и океана. – 1996. – № 1. – С. 78.

3. Безуглов Д.А., Рытиков С.Ю. Дифференцирование сигнала на фоне шума с применением максимально-правдоподобной оценки // Физические основы приборостроения. – 2012. – Т. 1. – № 3 (4). – С. 26–32.

4. Безуглов Д.А., Рытиков С.Ю., Швидченко С.А., Гаврин М.С., Гаврин Д.С. Выделение контуров изображений в информационных и управляющих системах с использованием метода вейвлет-преобразования // Нелинейный мир. – № 11 – 2012. – С. 846–852.

5. Безуглов Д.А., Рытиков С.Ю., Швидченко С.А. Метод вейвлет-дифференцирования в задаче выделения контуров // Успехи современной радиоэлектроники. – 2012. – № 6. – С. 52–57.

6. Безуглов Д.А., Скляров А.В., Забродин Р.А., Решетникова И.В. Алгоритмы оценивания негауссовских процессов на основе математического аппарата сглаживающих В-сплайнов // Известия высших учебных заведений. Северо-Кавказский регион. Серия: Естественные науки. – 2005. – № 4. – С. 99–106.

7. Безуглов Д.А., Скляров А.В., Забродин Р.А., Решетникова И.В. Субоптимальный алгоритм оценивания на основе аппарата сглаживающих В-сплайнов // Измерительная техника. – 2006. – № 10. – С. 14–17.

8. Безуглов Д.А., Цугурян Н.О. Дифференцирование результатов измерений сглаживающими кубическими В-сплайнами // Современные информационные технологии. – 2005. – № 1 (1). – С. 73–78.

9. Безуглов Д.А., Швидченко С.А. Информационная технология вейвлет-дифференцирования результатов измерений на фоне шума // Вестник компьютерных и информационных технологий. – 2011. – № 6 (84). – С. 42–45.

10. Швидченко С.А., Безуглов Д.А., Рытиков С.Ю., Решетникова И.В. Выделение контуров изображений с использованием метода вейвлет-дифференцирования. Часть 2 // Труды Северо-Кавказского филиала Московского технического университета связи и информатики. – 2012. – № 1. – С. 37–40.

11. Швидченко С.А., Безуглов Д.А., Рытиков С.Ю., Решетникова И.В. Выделение контуров изображений с использованием метода вейвлет-дифференцирования. Часть 1 // Труды Северо-Кавказского филиала Московского технического университета связи и информатики. – 2012. – № 1. – С. 33–36.

12. Швидченко С.В., Безуглов Д.А. Синтез алгоритмов дискретного вейвлет-анализа фрагментов изображений в условиях априорной неопределенности на случайном фоне // Успехи современной радиоэлектроники. – 2013. – № 5. – С. 031–038.

На сегодняшний день на рынке информационных технологий автоматизации обработки изображений широкую популярность получают системы машинного зрения. С помощью них можно решать широкий спектр задач, таких как создание систем распознавания печатных и рукописных текстов, биометрической идентификации, а также систем идентификации для перспективных информационных систем, например, используемых при наблюдении за охраняемыми объектами при осуществлении мероприятий, обеспечивающих собственную безопасность таможенных постов, при организации контроля над соблюдением режима зоны таможенного контроля, а также при обеспечении охраны объектов таможенной инфраструктуры.

Области применения цифровой обработки в настоящее время значительно расширяются, вытесняя аналоговые методы обработки сигналов и изображений. Методы цифровой обработки широко применяются в промышленности, искусстве, медицине, космосе. Они используются при автоматизации обнаружения и сопровождения объектов, распознавании образов, в таможенном деле. Отмеченное выше делает вполне очевидной актуальность проведения исследований существующих и создания новых методов цифровой обработки изображений, зарегистрированных на фоне шума

Как правило, анализ изображений делится на следующие этапы:

– фильтрация изображений;

– сегментация изображений;

– улучшение изображений.

Формирование изображений, улучшение качества и автоматизация обработки изображений, включая изображения, создаваемые электронными микроскопами, рентгеновскими аппаратами, томографами и т.д., являются предметом исследования и разработки. Сегодня в технике широко применяются системы формирования изображения, его преобразования в цифровую форму, визуализация и документирование путем введения в компьютер изображений с помощью специализированных устройств захвата видео.

В большинстве случаев процесс автоматической классификации проводится в три этапа:

1. Предварительная обработка, состоящая в максимальном приближении исследуемого изображения к эталонному или нормализованному. Чаще всего для изображений это пространственно-инвариантные операции, сдвиг, изменение яркости, изменение контраста, квантование и геометрические преобразования (изменение масштаба, поворот оси).

2. Выделение признаков, при которых функция, представляющая обработанное изображение, подвергается функциональному преобразованию, выделяющему ряд наиболее существенных признаков, которые кодируются действительными числами. Выделение признаков заключается в математических преобразованиях изображения, в зависимости от задачи анализа. Это может быть вычитание из эталона, вычитание постоянной составляющей для исключения мешающих теней, дифференцирование или автокорреляция для выделения контура, частотная фильтрация и многие другие.

3. Классификация признаков. Полученные в результате предыдущей операции наборы действительных чисел, описывающие выделенные признаки, сравниваются с эталонными числами, заложенными в память машины. ЭВМ на основании такого сравнения классифицирует изображение.

Одной из главных и наиболее сложных задач систем компьютерного зрения и теории распознавания образов является выделение контуров объектов на изображении. На сегодняшний день эта задача актуальна, в том числе, например, при решении проблемы идентификации автомобиля по регистрационному номерному знаку. Сложность этой задачи связана с наличием цифровых шумов на входных изображениях, полученных в процессе их регистрации, оцифровки, а также в результате воздействия различных факторов. Изображения в процессе формирования их изображающими системами обычно подвергаются воздействию различных случайных помех или шумов. Наиболее распространенным видом помех является случайный аддитивный шум, статистически независимый от сигнала.

Задачу идентификации автомобильного номера можно условно разделить на следующие подзадачи:

– подготовка исходного изображения – предварительная обработка исходного изображения, содержащего государственный регистрационный автомобильный номер, применение к изображению различных фильтров с целью улучшения качества для последующей локализации номерной пластины;

– локализация номерной пластины – получение координат номерной пластины на исходном изображении;

– сегментация и распознавание символов, принадлежащих номерной платине – в результате процесса сегментации на локализованной номерной пластине отделяются символы номера от общего фона, после чего происходит процесс их идентификации выбранным методом распознавания.

Реально существующие в настоящее время программы идентификации номерных знаков автомобилей предъявляют очень жесткие требования к качеству получаемых изображений, номер автомобиля должен размещаться в кадре целиком, угол вертикального наклона видеокамеры – не более 35–40°, угол наклона вглубь – не более 30°. Изображения должны быть четкими и не размытыми, размер символов для надежного распознавания должен быть не менее 14 пикселей в высоту. При настройке источника видеосигнала должно быть обеспечено качество изображения, пригодное для последующего анализа: номерной знак должен иметь высокую четкость и контрастность, изображение должно иметь широкий динамический диапазон яркости и не должно содержать сильных шумов. Выполнение этих требований в реальных условиях не всегда возможно. Поэтому в сложных условиях наблюдения существующие системы оказываются неработоспособны,

Таким образом, научная задача разработки высокоэффективных алгоритмов идентификации номерных знаков на фоне сильных шумов в настоящее время не решена в достаточной мере и является актуальной.

Задаче идентификации номерного знака предшествует операция выделения контуров. Решение задачи выделения контуров используется в промышленности при создании систем анализа изображений в сложных условиях наблюдения, при воздействии различных мешающих факторов, усложняющих процесс регистрации изображения и при отсутствии априорных сведений о виде фоновых шумов. Это значит, что методы и алгоритмы обработки информации с датчиков изображения должны учитывать наличие шумов различной природы, связанных с регистрацией изображений и сигналов в реальных системах.

При этом известные в настоящее время алгоритмы решения таких задач предполагают предварительную фильтрацию изображений, а затем решение задачи выделения контуров. При построении методов и алгоритмов фильтрации изображений требуется априорное знание характеристик искажающих помех. На практике в большинстве случаев такая информация отсутствует или является приближенной.

По своему характеру все операторы подчеркивания контуров являются различными модификациями дифференцирования двумерного поля по различным направлениям области определения [1, 2]. Как известно, при дифференцировании в самом деле в окрестности перепада функции яркости образуется пик, способствующий регистрации этой области. Однако также хорошо известно, что при дифференцировании сигналов с помехами происходит существенное усиление последних, что снижает отношение сигнал/шум и негативно отражается на получаемых результатах. Известные методы выделения контуров изображений, основанные на эвристических подходах и методах последовательного численного дифференцирования локальных областей изображения с помощью различных масок, как правило, не работоспособны в условиях сильных шумов.

Для решения проблемы влияния шумов на результат выделения контуров в данной работе рассматривается метод прямого и обратного вейвлет-дифференцирования. Предлагаемый подход заключается в аналитическом дифференцировании элементов изображения предложенным способом [4, 5, 6, 8]. В работе показано преимущество представленного метода по сравнению с известными на примере анализа серии различных изображений.

Модуль градиента интенсивности исследуемого изображения S(i, j) в терминах вейвлет-преобразования запишется в следующем виде:

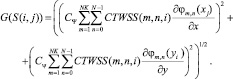(1)

Изображения в процессе формирования их изображающими системами обычно подвергаются воздействию различных случайных помех или шумов [7, 8, 9]. В качестве критериев качества в работе использованы следующие.

1. Среднеквадратическое отклонение eСКО:

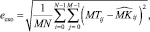(2)

где M, N – размерность матрицы изображения.

В качестве тестового изображения MT использовалось изображение контуров, полученное из незашумленного исследуемого изображения S детектором границ Canny. В дальнейшем на исходное изображение S накладывался аддитивный гауссовский шум и проводилось определение контуров предложенным методом вейвлет-дифференцирования и известным методом Собеля. При этом были получены изображения .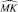

2. Отношение пиковый сигнал/шум SNR1:

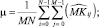
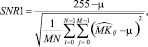(3)

где μ – среднее значение .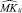

3. Отношение пиковый сигнал/шум SNR2 (с использованием в расчетах СКО фона):

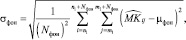(4)

где σ_фон – СКО фона;

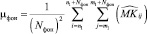– среднее значение фона; n1, m1 – координаты выбранной площадки фона размером N_фон×N_фон на исследуемом изображении ,

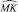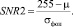(5)

Используя три критерия, в дальнейшем можно будет более адекватно оценить эффективность предложенных алгоритмов по сравнению с известными.

Рассмотрим подробнее алгоритмы вейвлет-дифференцирования с использованием вейвлетов MHAT, DOG и WAVE, полученные на основе разработанного ранее метода вейвлет-дифференцирования [3, 4, 5, 6]. В данном случае свойства вейвлет-преобразования позволяют отказаться от применения различных масок, то есть, по сути, отказаться от малоэффективных методов численного дифференцирования. Суть предлагаемого вейвлет-дифференцирования состоит в том, что исходное изображение сначала представляют в виде строк и столбцов. Затем вычисляют прямое вейвлет-преобразование строк и столбцов цифрового изображения, а затем формируют две матрицы и компонент градиента яркости в каждой точке изображения путем обратного вейвлет-преобразования, в котором в качестве ядра преобразования используют аналитические функции, описывающие производные используемых вейвлетов обратного преобразования по соответствующим координатам. В общем виде производные строки и столбца изображений могут быть записаны следующим образом:

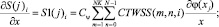(6)

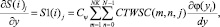i = 0...N, j = 0...N, (7)

где CTWSS(m, n, i) и CTWSC(m, n, j) соответственно коэффициенты прямого дискретного вейвлет-преобразования по строкам и столбцам матрицы изображения S(i, j); Cψ – постоянная зависящая от вида базисной вейвлет-функции [3, 4]; φ(x), φ(y) – функции вейвлет-преобразования.

В дискретном виде коэффициенты прямого дискретного вейвлет-преобразования по строкам и столбцам матрицы изображения S(i, j) запишутся в следующем виде:

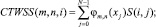(8)

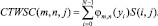(9)

Тогда выражение для квадрата градиента матрицы S(i, j) будет иметь следующий вид:

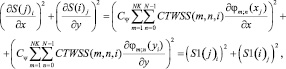i = 0...N, j = 0...N. (10)

Модуль градиента интенсивности исследуемого изображения S(i, j) в терминах вейвлет-преобразования запишется в виде (1).

В качестве одного из наборов тестовых изображений использовалась фотография номера автомобиля размером 512×512. Порядок проведения вычислительного эксперимента был следующим [7, 8, 9, 11, 12]. Исходное восьмибитное изображение размером 512×512, подвергалось воздействию аддитивного гауссовского шума с СКО σ = 5, 20, 30, 40, 50. Затем изображение было обработано детектором границ Собеля и с использованием вейвлет-преобразований [7, 8, 9, 10]. Результаты экспериментов приведены в сводной таблице.

Результаты вычислительных экспериментов

Выводы

Анализ результатов математического моделирования позволяет сделать следующие выводы. Предложенный метод обработки изображений позволяет эффективно идентифицировать номерные знаки автомобилей, искаженные шумом. Разработанные новый метод и алгоритмы вейвлет-дифференцирования изображений на фоне шума с использованием дискретного вейвлет-преобразования позволяют повысить отношение пиковый сигнал – шум на 4,8–9,6 дБ и в 3–4 раза уменьшить среднеквадратическое отклонение ошибки.

Библиографическая ссылка