Система контроля заправки предназначена для выдачи контактных команд на пульт управления заправкой при достижении компонентами топлива во время заправки определенных значений в баках третьей ступени ракеты космического назначения среднего класса серии «Союз». Кроме того, система позволяет вести визуальный контроль за поведением уровней компонентов топлива в баках в пределах ±10 мм от точки «Уровень».
Система состоит из блока контроля заправки (БКЗ); пульта контроля указателей наполнения (ПК) с комплектом кабелей; пульта проверки (ПП) БКЗ и ПК с комплектом кабелей; имитатора (И) для проверки бортовой кабельной сети.
Целью исследования является разработка математической модели расчета надежности системы контроля заправки, использующейся для оценки готовности третьей ступени ракеты космического назначения (РКН) среднего класса.
Исходные предположения и допущения метода исследования
Система контроля заправки РКН является сложной системой многократного циклического применения.
Система задействована на этапе заправки РКН, для которого заданы требования по надежности функционирования СК – вероятность успешного функционирования (вероятность безотказной работы) СК на данном этапе должна быть не ниже 0,95.
Приемлемый уровень вероятности недостижения предельного состояния системой определяется исходя из его вклада в вероятность недостижения предельного состояния стартового комплекса в целом на каждом из этапов функционирования.
Разработка математической модели достижения предельного состояния системы
Дерево достижения предельного состояния представляет собой графическое отображение причинно-следственных связей между наступлением предельного состояния объекта с отказами (переходами в предельное состояние) его элементов и другими событиями [4]. При графическом построении деревьев отказов системы использовались обозначения логических операторов, представленные на рис. 1.
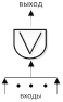
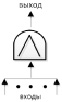
Рис. 1. Символы логических операторов «ИЛИ», «И» соответственно, используемые для графического построения дерева отказов системы
Остаточный ресурс (после наработки) – наработка объекта, начиная с момента до перехода в предельное состояние при установленных режимах применения и условиях эксплуатации [3].
Наработка – продолжительность или объем работы объекта [3]. Наработка может измеряться в единицах времени или объема выполненной работы. Для оборудования системы, с учетом специфики их применения, наиболее удобно измерять наработку в единицах времени.
Предельное состояние (ПС) – состояние объекта, при котором его дальнейшее применение по назначению недопустимо или нецелесообразно, либо восстановление его исправного или работоспособного состояния невозможно или нецелесообразно [3].
Критериями предельного состояния объекта являются установленные в стандартах и конструкторских документах признаки состояния объекта, при котором его дальнейшая эксплуатация невозможна, нецелесообразна или опасна [6].
В основу формирования критериев предельного состояния оборудования системы целесообразно положить признаки, характеризующие невозможность восстановления работоспособного состояния.
Невозможность восстановления работоспособного состояния объекта определяется возникновением неустранимых (в данных условиях) отказов, вызывающих прекращение функционирования объекта.
Под неустранимостью отказа оборудования системы понимается невозможность устранения отказа без прерывания применения оборудования по назначению и проведения определенных действий, вызывающих длительные перерывы функционирования оборудования и необходимость вложения значительных материальных и финансовых средств (проведение среднего и капитального ремонта, модернизация средств, разработка и изготовление блоков аппаратуры на новой элементной базе, демонтаж и замена стационарных кабельных сетей и т.п.).
На основании описанного выше могут быть выделены следующие критерии предельного состояния системы:
1. Приемлемый уровень вероятности недостижения предельного состояния системой определяется исходя из его вклада в вероятность недостижения предельного состояния в целом на каждом из этапов функционирования.
2. Допустимое количество составных элементов системы, достигших предельного состояния, определяется на основе расчета вероятностной функции достижения предельного состояния.
Вероятности событий, являющиеся компонентами вероятностной функции достижения предельного состояния (ВФ ДПС), определяются исходя из физической природы процессов, приводящих к наступлению каждого из них. Численные значения вероятностей наступления каждого события рассчитываются на основе физических, физико-статистических или статистических моделей, в зависимости от возможности получения исходных данных и характера описываемых процессов. Исходными данными для расчетов на основе физических и физико-статистических моделей являются параметры технического состояния, полученные в ходе визуального и измерительного контроля, в том числе с использованием приборов неразрушающего контроля.
В качестве математической модели достижения предельного состояния системой следует рассматривать критерий [5]
G:PНДПС ≥ γ,
где PНДПС – вероятность недостижения предельного состояния системой; γ – условный приемлемый уровень вероятности недостижения предельного состояния (гамма), принятый для данной системы.
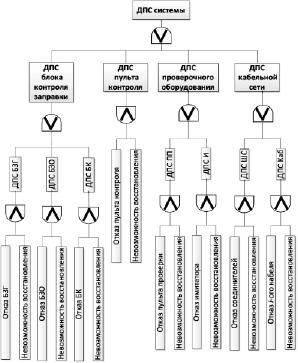
Рис. 2. Дерево достижения предельного состояния системы
Для более подробного представления математической модели достижения предельного состояния системой необходимо получить вероятностную функцию достижения предельного состояния, которая может быть получена путем формализации «дерева» достижения предельного состояния (рис. 2):
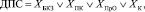 (1)
(1)
где ДПС – достижение предельного состояния системы; XБКЗ – достижение предельного состояния блока контроля заправки; XПК – достижение предельного состояния пульта контроля указателей наполнения; XПрО – достижение предельного состояния проверочного оборудования; XК – достижение предельного состояния кабельной сети;
Логическая функция ДПС блока контроля заправки будет иметь вид:
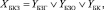 (2)
(2)
где YБЗГ – достижение предельного состояния блока заправки горючего; YБЗО – достижение предельного состояния блока заправки окислителя; YБК – достижение предельного состояния блока коммутации
В свою очередь:
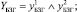 (3)
(3)
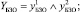 (4)
(4)
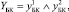 (5)
(5)
где индексами y1 обозначены переходы соответствующих элементов системы в неработоспособное состояние, индексами y2 – невозможность восстановления работоспособного состояния.
Логическая функция ДПС пульта контроля указателей наполнения будет иметь вид
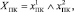 (6)
(6)
где 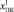 – переход пульта контроля указателей наполнения в неработоспособное состояние;
– переход пульта контроля указателей наполнения в неработоспособное состояние; 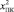 – невозможность восстановления работоспособного состояния.
– невозможность восстановления работоспособного состояния.
Логическая функция ДПС проверочного оборудования будет иметь вид
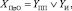 (7)
(7)
где YПП – переход пульта проверки БКЗ и ПК в неработоспособное состояние; YИ – переход имитатора для проверки бортовой кабельной сети в неработоспособное состояние.
В свою очередь:
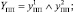 (8)
(8)
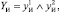 (9)
(9)
где индексами y1 обозначены переходы соответствующих элементов системы в неработоспособное состояние, индексами y2 – невозможность восстановления работоспособного состояния.
Логическая функция ДПС кабельной сети будет иметь вид
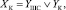 (10)
(10)
где YШС – переход штепсельных разъемов в неработоспособное состояние; YК – переход кабелей в неработоспособное состояние;
В свою очередь:
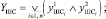 (11)
(11)
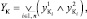 (12)
(12)
где индексами y1 обозначены переходы соответствующих элементов системы в неработоспособное состояние, индексами y2 – невозможность восстановления работоспособного состояния.
После объединения выражений (1)–(12) получим
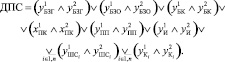
Тогда НДПС = ¬ДПС будет определять логическую функцию недостижения предельного состояния системой [1]:
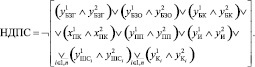
Соответствующая вероятностная функция недостижения предельного состояния системой будет являться произведением вероятностей событий, противоположных событиям, которые в свою очередь являются бинарными конъюнкциями [2].
Вероятностная функция недостижения предельного состояния имеет вид [1]
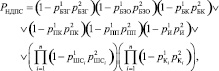
где 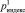 – вероятность отказа узла, определенного индексом;
– вероятность отказа узла, определенного индексом; 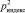 – вероятность невозможности восстановления работоспособного состояния узла указанного индекса.
– вероятность невозможности восстановления работоспособного состояния узла указанного индекса.
Результаты исследования и их обсуждение
При известных значениях вероятностей отказа конечных элементов дерева предельного состояния расчет вероятности безотказной работы системы не составляет труда. На основе статистических данных, полученных при эксплуатации системы, решается задача прогнозирования показателей надежности при выполнении работ по продлению назначенных показателей ресурса стартового комплекса, определяется перечень мероприятий, позволяющих обеспечить фактический ресурс системы не ниже требуемого согласно эксплуатационной и конструкторской документации.
По результатам определения рационального перечня мероприятий оформляется план мероприятий по обеспечению эксплуатации системы на продлеваемый период.
Выводы
Результаты расчета надёжности системы контроля заправки могут быть использованы для дальнейшего расчета и прогнозирования вероятности безотказной работы системы на достаточно длительный период эксплуатации, что позволит прогнозировать эксплуатационные затраты на применение системы и свести к минимуму вероятность критичных отказов как системы, так и стартового комплекса в целом.
Библиографическая ссылка
Басотин Е.В., Витюк В.Л., Миронов Е.А., Мосиенко А.Г., Суворов А.Н. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСЧЕТА ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ СИСТЕМЫ КОНТРОЛЯ ЗАПРАВКИ РАКЕТЫ КОСМИЧЕСКОГО НАЗНАЧЕНИЯ // Фундаментальные исследования. 2016. № 10-2. С. 254-258;URL: https://fundamental-research.ru/ru/article/view?id=40841 (дата обращения: 07.03.2026).



