Решение задач управления динамическими объектами предполагает использование математической модели исследуемого процесса. Математические модели, полученные на основе физических или каких-либо других законов, в практических приложениях, как правило, не всегда точно отражают исследуемые процессы. Поэтому для уточнения структуры и параметров математической модели применяются различные алгоритмы идентификации и алгоритмы построения моделей [1, 2, 4, 5]. Алгоритмы построения моделей позволяют получить высокоточные математические модели исследуемых объектов, однако их использование для управления затруднительно, так как структура модели заранее неизвестна и вопрос проверки устойчивости требует дополнительных исследований. Алгоритмы идентификации позволяют определить отдельные параметры матрицы модели, структура которой задана априори. Для решения задачи идентификации нелинейных объектов разработано довольно много подходов и методов [3, 4, 6, 7]. На современном этапе возросли требования к точностным характеристикам применяемых алгоритмов идентификации. В связи с этим модифицируются классические подходы к решению задачи идентификации нелинейных систем с целью повышения их точности и уменьшения ограничений применения [1, 6, 10], а также универсальные поисковые методы, которые требуют минимальной априорной информации об идентифицируемой системе, но сложны в реализации.
В настоящей работе исследована проблема идентификации нелинейных систем. В качестве основной трудности данной проблемы можно назвать необходимость обработки большой базы данных, характеризующей работу идентифицируемой системы. Конструктивным подходом в решении данной задачи является использование фильтрующей структуры в виде последовательности Вольтерра [3, 6, 8]. Однако одной из главных причин достаточно редкого применения методики фильтрации Вольтерра на практике является значительная сложность, связанная с реализацией фильтров Вольтерра [9, 11]. Таким образом, главной задачей является нахождение упрощений в разработке и реализации фильтра Вольтерра.
Фильтр Вольтерра 2-го порядка
Возьмем фильтр Вольтерра 2-го порядка (ФВ2), который состоит из параллельной комбинации линейного и квадратичного фильтров [8, 9]:
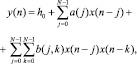 (1)
(1)
где {a(j)} и {b(j, k)} называются линейным и квадратичным весом соответственно, а N указывает длину фильтра (предполагается симметричность квадратичных весов фильтра, т.е. b(j,k) = b(k,j)).
Далее возьмем, что x(n) и s(n) – это случайные процессы с нулевым математическим ожиданием с дискретным параметром n. Нужно найти веса фильтра, которые минимизируют среднюю квадратичную ошибку (СКОШ) между s(n) и выходом фильтра y(n), т.е.
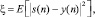 (2)
(2)
где предполагается строгая стационарность s(n) и x(n) с нулевым математическим ожиданием.
Первым шагом в определении минимума среднеквадратичной ошибки является требование бездрейфового выхода фильтра. Другими словами, должно быть E[y(n)] = 0, так как основной сигнал имеет нулевое математическое ожидание.
Тогда имеем следующее соотношение между h0 и b(j, k):
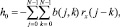 (3)
(3)
где 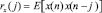 обозначает автокорреляционную функцию x(n). Важно включение члена нулевого порядка h0. Некоторые из предыдущих исследователей не имели выхода нулевого порядка, но без этого выход минимальной средней квадратичной ошибки фильтра Вольтерра не является обязательно бездрейфовым и ошибка имеет, следовательно, тенденцию к увеличению, в отличие от фильтра Вольтерра 2-го порядка с h0, выраженном в (3).
обозначает автокорреляционную функцию x(n). Важно включение члена нулевого порядка h0. Некоторые из предыдущих исследователей не имели выхода нулевого порядка, но без этого выход минимальной средней квадратичной ошибки фильтра Вольтерра не является обязательно бездрейфовым и ошибка имеет, следовательно, тенденцию к увеличению, в отличие от фильтра Вольтерра 2-го порядка с h0, выраженном в (3).
Подставляя в (1) выражение (3), получим формулу для определения фильтра Вольтера 2-го порядка:
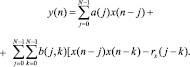 (4)
(4)
Следующий шаг – определение линейных и квадратичных весов фильтра a(j) и b(j, k), которые определяют минимум среднеквадратичной ошибки.
Выведем простое решение для оптимального фильтра Вольтерра 2-го порядка в предположении, что на входе фильтра гауссион. Во-первых, заметим, что (4) может быть переписано в виде [8, 9]:
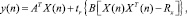 (5)
(5)
где tr – след матрицы В;
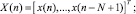
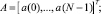
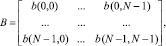
Rx указывает на N×N матрицу от x(n), где rx(j, k) = rx(j – k) – автокорреляционная функция входного сигнала x(n). A и B – операторы линейного и квадратичного фильтра соответственно.
Перед выводом решения определим кросс-корреляционную rsx(j) и кросс-бикорреляционную tsx(j, k) функции между x(n) и s(n) следующим образом:
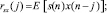
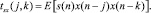
Поскольку предполагается, что s(n) и x(n) – строго стационарны, то как rsx(j), так и tsx(j, k) являются независимыми от переменной n. Кросс-бикорреляционная функция tsx(j, k) определяет статистическую зависимость между s(n) и x(n), которая является критичной при нахождении оптимального квадратичного оператора фильтра. Кроме того, надо сказать, что кросс-бикорреляционная функция является симметричной, т.е. tsx(j, k) = tsx(k, j).
В матричной форме кросс-корреляционную и кросс-бикорреляционную функцию можно записать следующим образом:
Rsx = [rsx(0), …, rsx(N – 1)]T;
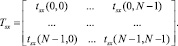
Отсюда линейный и квадратичный операторы фильтра Вольтерра 2-го порядка с минимальной среднеквадратичной ошибкой определяются следующим образом:
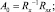 (6)
(6)
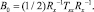 (7)
(7)
Адаптивный алгоритм реализации
Алгоритм наименьшего среднего квадратического (НСК) для линейного фильтра хорошо известен и представляется в виде
A(n + 1) = A(n) – 2μAe(n)X(n). (8)
Здесь A(n) – оператор линейного фильтра в момент n и e(n) = AT(n)X(n) – s(n) – остаточная ошибка фильтра. Также μA – положительная константа, от которой зависит устойчивость и сходимость алгоритма.
Рассматривая адаптивную реализацию ФВ2, можно заметить, что оператор линейного фильтра может быть скорректирован, используя алгоритм (8), за исключением остаточной ошибки, представляемой в виде:
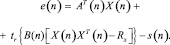 (9)
(9)
Можно увидеть, что предыдущие результаты для стандартного НСК-алгоритма остаются в силе. Следовательно, необходимо рассмотреть только адаптацию оператора квадратичного фильтра.
Однако в (9) следует отметить, что выражение нулевого порядка tr{B(n)Rx} не является константой при адаптивной реализации. Вспомним, что выражение нулевого порядка необходимо для вычитания математического ожидания выходного значения квадратичного фильтра из выходного значения ФВ2 [9]. Следовательно, когда Rx неизвестно, рекурсивный алгоритм оценки (например, НЧ-фильтр) для уровня среднего выходного значения квадратичного фильтра можно заменить выражением нулевого порядка.
Для упрощения не будем изменять выражение нулевого порядка, поэтому его адаптация рассматриваться не будет. Как расширение НСК-алгоритма рассмотрим следующий адаптивный алгоритм для оператора квадратичного фильтра:
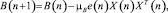 (10)
(10)
где μB – положительная константа.
Концептуально данный алгоритм имеет под собой основание, т.к.
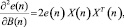
и его реализация вполне приемлема.
Первая аппроксимация должна допускать, что A(n) и B(n) – независимы от пары {s(n), X(n)}. Тогда мы имеем
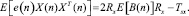
Таким образом, если мы определим δB(n) = B(n) – B0, где B0 – оптимум оператора квадратичного фильтра, определяемого с минимальной среднеквадратичной ошибкой следующим образом: 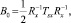 то математическое ожидание, взятое от обеих частей (10), даст
то математическое ожидание, взятое от обеих частей (10), даст
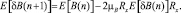 (11)
(11)
Заметим, что математическое ожидание оператора квадратичного фильтра сходится к оптимуму B0 тогда и только тогда, когда 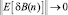 при n → ∞.
при n → ∞.
Действительно, если 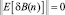 для некоторого n, то это остается справедливым и для всех других n. Для
для некоторого n, то это остается справедливым и для всех других n. Для 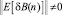
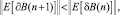 если размер шага μB выбирается следующим образом:
если размер шага μB выбирается следующим образом:
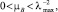 (12)
(12)
где λmax – наибольшее собственное значение матрицы R.
Отсюда средняя ошибка между B(n) и B0 монотонно снижается до 0 с увеличением времени. Далее при детальном рассмотрении процесса адаптации можно увидеть, что каждый элемент матрицы E[δB(n)] состоит из набора компонент вида e–αt, в которых самое быстрое и самое медленное затухание определяется λmax и λmin.
В адаптивной реализации ФВ2 флуктуации операторов линейного и квадратичного фильтров добавляют некоторую дополнительную СКОШ в выходное значение фильтра даже при устойчивом положении адаптационного процесса. Таким образом, асимптотическая СКОШ адаптивного ФВ2 в общем случае больше, чем СКОШ оптимального ФВ2. Для оценки остатка СКОШ запишем СКОШ адаптивного ФВ2 в виде
ξ(n) = ξopt + ξA(n) + ξB(n);
причем остаток СКОШ линейного и квадратичного представляется:
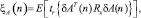
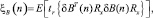
где δA(n) = A(n) – A0 и δB(n) = B(n) – B0 – суть отклонения A(n) и B(n) от их оптимальных значений.
Затем, получим следующие ограничения для остатка СКОШ:
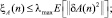
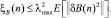
Так как нас интересуют главным образом асимптотические значения остатка СКОШ после достижения адаптивным процессом своего устойчивого состояния, то мы допускаем, что A(n) и B(n) близки к A0 и B0 соответственно. Отсюда выбираем μA и μB так, чтобы 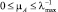 и
и 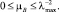
Таким образом, имеем
δA(n) = –2μAe(n)X(n)
и
δB(n) = –μBe(n)X(n)XT(n).
Кроме того, при данных условиях как X(n), так и X(n)XT(n) не коррелирует с остаточной ошибкой e(n).
Следовательно, получаем следующие ограничения для асимптотического остатка СКОШ (АОСКОШ):
ξA ≤ 4μAξoptNrx(0);
ξB ≤ 3μBξopt[Nrx(0)]2.
Заключение
В работе представлены способы реализации фильтра Вольтерра 2-го порядка, связанные с упрощением его реализации. Показано, что простое решение для оптимального ФВ2, его адаптивный алгоритм могут дать эффективные гибкие подходы для разработки и реализации ФВ2. С другой стороны, распространение полученных результатов на фильтр Вольтерра более высокого порядка является интересным объектом дальнейшего исследования.
Библиографическая ссылка
Цибизова Т.Ю. АДАПТИВНЫЙ АЛГОРИТМ ИДЕНТИФИКАЦИИ НЕЛИНЕЙНЫХ СИСТЕМ РЯДАМИ ВОЛЬТЕРРА // Фундаментальные исследования. 2016. № 10-1. С. 102-106;URL: https://fundamental-research.ru/ru/article/view?id=40816 (дата обращения: 07.02.2026).



