Конструкции, армированные дискретными волокнами, должны быть обеспечены с требуемой надежностью от возникновения всех видов предельных состояний расчетом, выбором показателей качества материалов, назначением размеров и конструированием согласно указаниям СНиП 52-01 и СП 52-104 2006*. Учет влияния технологических факторов и их изменчивости на надежность конструкций может быть выполнен только с помощью вероятностных расчетов, учитывающих взаимодействие случайных величин, – следовательно, разработка вероятностного алгоритма представляет собой одну из главных задач в организации системы контроля качества выпускаемой продукции. Кроме того, разработка вероятностных алгоритмов и написание программы по оценке надежности элементов конструкций необходимы для выполнения численного моделирования по изучению влияния изменчивости разных технологических факторов на их эксплуатационную пригодность.
Испытания конструкций дают возможность оценить их пригодность по нескольким группам предельных состояний: по прочности, по жесткости и по трещиностойкости. Соответственно, в качестве основных критериев при оценке эксплуатационной пригодности [1, 3, 4] изгибаемых элементов принимают, как правило, следующие показатели:
а) по прочности дисперсно-армированного бетона (среднее значение нагрузки F при испытаниях не должно быть ниже заданной максимальной нагрузки Fult):
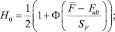 (1)
(1)
б) по жесткости (среднее значение прогиба f изгибаемого элемента не должно превышать критического fult):
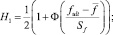 (2)
(2)
в) по трещиностойкости (среднее значение величины раскрытия трещины в центральном нормальном сечении изгибаемого элемента acrc не должно превышать критического значения acrc,ult):
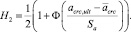 (3)
(3)
Здесь SF, Sf, Sa – среднеквадратичные отклонения соответственно величин F, f, acrc; Φ(x) – функция Лапласа:
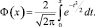 (4)
(4)
Важным вопросом является назначение величин H0, H1, H2, определяющих материалоемкость конструкций. На основании расчетных прочностных характеристик материалов, приведенных в нормах проектирования (ГОСТ 27751-88, СНиП 52-01, СНиП 2.01.07, СП 52-104 2006* и др.) ж/б и ФБ конструкций, уровни надежности по каждому предельному состоянию варьируются от 0,8 до 0,98. Согласно работам [3, 4] можно принять за требуемые следующие значения величин H0 = 0,95, H1 = 0,95, H2 = 0,90.
Большинство теоретических исследований [3, 4, 7] в области оценки надежности ж/б конструкций показывают, что наиболее эффективными методами для разработки вероятностных алгоритмов являются методы: линеаризации функций, статистического моделирования (Монте-Карло), статистических испытаний. Метод статистического моделирования – это численный вероятностно-статистический метод решения математических задач, основанный на многократном моделировании случайных величин или процессов и последующем построении статистических оценок для искомых величин.
При использовании метода статистического моделирования [3, 7] производится достаточно большое число (n = 10000...30000) статистических испытаний по схеме Бернулли, т.е. при каждом испытании генерируются случайные реализации всех исходных величин согласно их плотности распределения вероятностей.
При разыгрывании случайных величин на ЭВМ используется стандартная функция rand(x) для генерирования случайных равномерно распределенных чисел в интервале [0; 1]. Для получения случайных чисел с нормальным законом распределения [3] при математическом ожидании М = 0 и дисперсии D = l могут использоваться следующие зависимости:
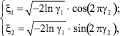 (5)
(5)
где γ1, γ2 – два независимых случайных числа с равномерным распределением; ξ1, ξ2 – два сопряженных числа с нормальным законом распределения (математическое ожидание М = 0 и дисперсия D = l).
Для исходных случайных величин с конкретным значением M и D перерасчет производится по формуле
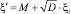 . (6)
. (6)
Далее с учетом полученных исходных величин по основной, математической модели производится N раз детерминированный расчет, т.е. расчет элементов по прочности бетона, расчет прогиба и ширины раскрытия трещин. Сравнение несущей способности с действующими усилиями в изгибаемом элементе определяет одно из возможных состояний системы в целом. Статистическая обработка совокупности таких состояний, число которых измеряется десятками тысяч, позволяет сделать соответствующие прогнозы. Для этого определяются статистические характеристики величин по следующим формулам:
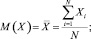
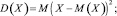
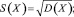
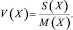 (7)
(7)
Здесь X – случайная величина; M(X) – среднее значение (математическое ожидание) случайной величины; N – количество испытаний; D(X) – дисперсия случайной величины: S(X) – среднеквадратическое отклонение случайной величины; V(X) – коэффициент вариации случайной величины.
Для статистической обработки и построения плотностей распределения прочностных характеристик матрицы и дискретных волокон использовался разработанный комплекс программ по оценке напряженно-деформированного состояния и оценки надежности изгибаемых элементов (SFRC.exe). Каждая характеристика при своем коэффициенте вариации разыгрывалась по 2·105 раз.
Экспериментальные исследования прочностных характеристик бетонов [5] позволили определить величину вариации призменной прочности бетона V(Rb); для разного класса и составов бетона значения коэффициента вариации лежали в пределах от 10 до 16 %.
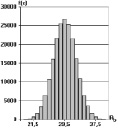
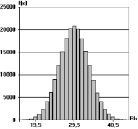
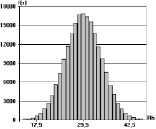
а б в
Рис. 1. Гистограммы плотностей распределения прочности бетона при различных коэффициентах вариации: а – V = 10 %; б – V = 13 %; в – V = 16 %
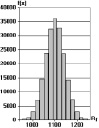
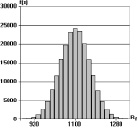
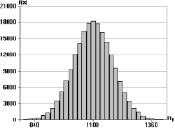
а б в
Рис. 2. Гистограммы плотностей распределения прочности стальных волокон при различных коэффициентах вариации: а – V = 4 %; б – V = 6 %; в – V = 8 %
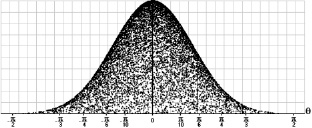
Рис. 3. Первые 104 результатов моделирования значений угла ориентации дискретного волокна в нормальном сечении изгибаемого элемента
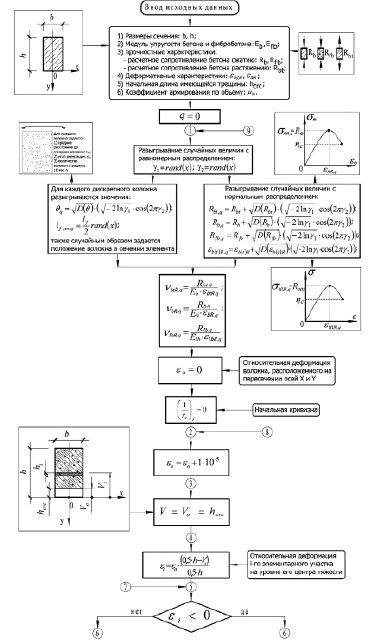
Рис. 4. Алгоритм программы SFRC – оценка надежности изгибаемых элементов, армированных дискретными волокнами, на основе вероятностной математической модели (часть 1)
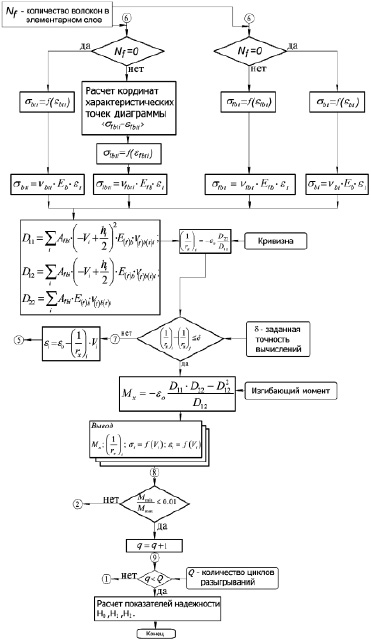
Рис. 5. Алгоритм программы SFRC – оценка надежности изгибаемых элементов, армированных дискретными волокнами, на основе вероятностной математической модели (часть 2)
Результаты 2·105 разыгрываний призменной прочности бетона при коэффициентах вариации: V(Rb) = 10 %, V(Rb) = 13 %, и V(Rb) = 16 % представлены в виде гистограмм на рис. 1. Среднее значение прочности бетона Rb = 29,5 МПа.
Коэффициент вариации предельной прочности фибры при растяжении оказался равным V(Rf) ≈ 4–8 %. Результаты 2·105 разыгрываний предельной прочности стального волокна при коэффициентах вариации: V(Rf) = 4 %, V(Rf) = 6 %, и V(Rf) = 8 % представлены в виде гистограмм на рис. 2. Среднее значение предельной прочности волокна Rf = 1100 МПа.
Анализ экспериментальных образцов после испытаний натурных конструкций из фибробетона [5] позволил определить величину среднеквадратичного отклонения угла ориентации волокон в нормальном сечении образцов: S(θ) ≈ 0,45 рад. На рис. 3 приведены результаты первых 104 разыгрываний угла ориентации дискретного волокна. Среднее значение угла ориентации волокна θ = 0 рад.
Распределение значений длин заделки дискретных волокон относительно нормального сечения изгибаемого элемента принято равномерным со средним значением, равным 15 мм, и крайними значениями 0 и 30 мм.
При сопоставлении фактических и теоретических значений основных статистических характеристик призменной прочности бетона, прочности волокон, их ориентации и положения относительно нормального сечения изгибаемого элемента можно отметить, что фактические значения, полученные по результатам численного моделирования, достаточно близки к теоретическим: расхождения составляют 2–4 %.
На основе математической нелинейно-деформационной модели разработаны вероятностный алгоритм и программа для ЭВМ по оценке надежности фибробетонных балок, работающих на изгиб, с учетом физической нелинейности материалов «SFRC.exe», которая реализует метод статистического моделирования. Вероятностный расчет состоит в определении статистических характеристик прочности, жесткости и трещиностойкости исследуемых элементов конструкции при проведении большого количества статистических испытаний, связанных с моделированием исходных случайных величин. Для определения этих характеристик на каждом этапе разыгрываний проводится детерминированный расчет по нелинейно-деформационной модели [2]. В результате программа выдает показатели надежности изгибаемых элементов, армированных стальными дискретными волокнами, по прочности, жесткости и трещиностойкости. Данные показатели позволяют судить об эксплуатационной пригодности исследуемых элементов конструкций. Блок-схема алгоритма программы представлена на рис. 4 и 5.
Библиографическая ссылка
Корнеев А.М., Бузина О.П., Суханов А.В., Шипулин И.А. ВЕРОЯТНОСТНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОЦЕНКИ НАЧАЛЬНОЙ НАДЕЖНОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ, ДИСПЕРСНО-АРМИРОВАННЫХ ДИСКРЕТНЫМИ ВОЛОКНАМИ // Фундаментальные исследования. 2016. № 9-3. С. 489-494;URL: https://fundamental-research.ru/ru/article/view?id=40771 (дата обращения: 01.03.2026).



